Resistor con dos capas

De Laplace

Contenido

1 Enunciado
2 Densidades de corriente y campos
3 Intensidad de corriente
4 Carga libre
- 4.1 Densidades
- 4.2 Cargas
5 Potencia y energía
- 5.1 Potencia
6 Energía eléctrica
7 Solución mediante el circuito equivalente

1 Enunciado

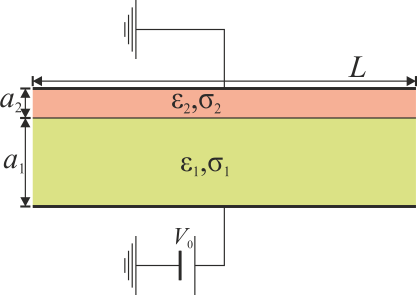
Se tiene un dispositivo formado por dos placas metálicas perfectamente conductoras, de sección cuadrada de lado 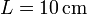$L=10\,\mathrm{cm}$ situadas paralelamente a 4 mm de distancia

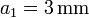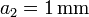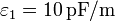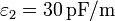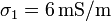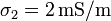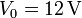Entre las placas se encuentran dos capas de dieléctricos no ideales de espesor $a_1=3\,\mathrm{mm}$ y $a_2=1\,\mathrm{mm}$ , respectivamente, de permitividades $\varepsilon_1 = 10\,\mathrm{pF}/\mathrm{m}$ y $\varepsilon_2=30\,\mathrm{pF}/\mathrm{m}$ y conductividades $\sigma_1=6\,\mathrm{mS}/\mathrm{m}$ y $\sigma_2=2\,\mathrm{mS}/\mathrm{m}$ . Se aplica un voltaje constante entre las placas $V_0 = 12\,\mathrm{V}$ .

Determine el valor de la densidad de corriente, el campo eléctrico y el vector desplazamiento en todos los puntos entre las placas.
Halle la intensidad de corriente que atraviesa el dispositivo.
Calcule las densidades de carga libre en todos los medios y superficies del sistema, así como la carga libre total acumulada en cada uno de los medios y superficies.
Halle la potencia disipada y la energía almacenada en el sistema.

2 Densidades de corriente y campos

Este sistema es uno de corrientes estacionarias, al estar las placas sometidas a una diferencia de potencial constante. Por ello, lo que va a determinar la distribución de los campos son las conductividades de los medios. El sistema equivale a dos resistencias puestas en serie para el cálculo de la densidad de corriente y el campo eléctrico.

Al tratarse de dieléctricos no ideales, la carga puede fluir por el interior de ellos y acumularse en la interfaces entre los medios, de forma que en $z = a 1$

$\mathbf{n}\cdot[\mathbf{D}]=\sigma_l\neq 0$

Esto implica igualmente que el sistema no es equivalente a un par de condensadores puestos en serie, ya que esto requiere que no haya carga neta en el nodo en que se conectan. Más adelante veremos la solución empleando un circuito equivalente.

En principio tenemos, para cada medio, las ecuaciones

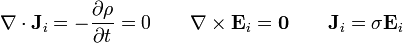
$\nabla\cdot\mathbf{J}_i = -\frac{\partial\rho}{\partial t} = 0\qquad\nabla\times\mathbf{E}_i = \mathbf{0}\qquad \mathbf{J}_i=\sigma\mathbf{E}_i$

Dado que la anchura de las placas es mucho mayor que la distancia entre ellas y que la interfaz es también paralela a las placas podemos suponer que los campos van en la dirección perpendicular a las placas, que tomaremos como eje Z

$\mathbf{E}_i = E_i\mathbf{u}_z\qquad\mathbf{J}_i = J_i\mathbf{u}_z$

Al sustituir esto en las ecuaciones diferenciales anteriores el resultado es, como en otros problemas, que las distribuciones de campo son uniformes en cada uno de los medios (aunque pueden tener un valor diferente en cada uno de ellos).

Queda hallar el valor de las constantes $E 1$ y $E 2$ . Para ello tenemos, en primer lugar, que la diferencia de potencial entre placas es $V 0$

$V_0 = \int_0^{a_1+a_2}E\,\mathrm{d}z = \int_0^{a_1}E\,\mathrm{d}z + \int_{a_2}^{a_1+a_2}E\,\mathrm{d}z = E_1a_1+E_2a_2$

En segundo lugar tenemos que en el estado estacionario no cambia la carga acumulada en la interfaz aentre los medios

$\mathbf{n}\cdot[\mathbf{J}] = -\frac{\partial\sigma_s}{\partial t} = 0\qquad\Rightarrow\qquad J_1 = J_2=J_0$

esto es, la densidad de corriente es la misma en las dos regiones. Hallamos el valor de J_0 sustituyendo en la ecuación anterior

$E_1 = \frac{J_0}{\sigma_1}\qquad E_2 = \frac{J_0}{\sigma_2}\qquad a_1\frac{J_0}{\sigma_1}+a_2\frac{J_0}{\sigma_2}=V_0$

Despejando

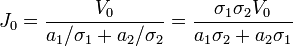
$J_0=\frac{V_0}{a_1/\sigma_1+a_2/\sigma_2}= \frac{\sigma_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}$

Por tanto, la densidad de corriente en los dos medios es, sustituyendo los valores numéricos,

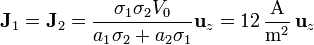
$\mathbf{J}_1 = \mathbf{J}_2 = \frac{\sigma_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 12\,\frac{\mathrm{A}}{\mathrm{m}^2}\,\mathbf{u}_z$

El campo eléctrico en la capa inferior vale

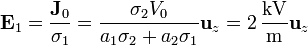
$\mathbf{E}_1 = \frac{\mathbf{J}_0}{\sigma_1} = \frac{\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 2\,\frac{\mathrm{kV}}{\mathrm{m}}\mathbf{u}_z$

y en la superior

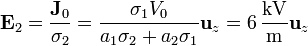
$\mathbf{E}_2 = \frac{\mathbf{J}_0}{\sigma_2} = \frac{\sigma_1V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 6\,\frac{\mathrm{kV}}{\mathrm{m}}\mathbf{u}_z$

De aquí obtenemos que el potencial en la interfaz vale

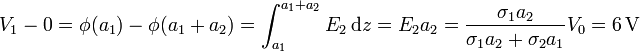
$V_1 - 0 = \phi(a_1) -\phi(a_1+a_2) = \int_{a_1}^{a_1+a_2}E_2\,\mathrm{d}z = E_2a_2 = \frac{\sigma_1a_2}{\sigma_1a_2+\sigma_2a_1}V_0 = 6\,\mathrm{V}$

Una vez que tenemos el campo eléctrico, el vector desplazamiento es inmediato. En el medio inferior

$\mathbf{D}_1 = \varepsilon_1\mathbf{E}_1 = \frac{\varepsilon_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z= 20\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

y en el superior

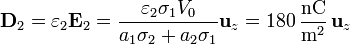
$\mathbf{D}_2 = \varepsilon_2\mathbf{E}_2 = \frac{\varepsilon_2\sigma_1V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z= 180\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

3 Intensidad de corriente

Puesto que estamos en el estado estacionario, la corriente que llega por el cable es la misma que atraviesa los materiales, e igual al flujo de la densidad de corriente a través de una sección transversal del medio óhmico (cualquiera de los dos, pues la densidad de corriente es la misma en ambos)

$I = \int_S \mathbf{J}\cdot\mathrm{d}\mathbf{S} = \int_0^L \int_0^L (J_0\mathbf{u}_z)\cdot(\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_z) = J_0L^2$

Sustituyendo el valor de la densidad de corriente

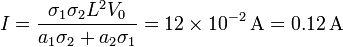
$I = \frac{\sigma_1\sigma_2L^2V_0}{a_1\sigma_2+a_2\sigma_1} = 12\times 10^{-2}\,\mathrm{A}=0.12\,\mathrm{A}$

4 Carga libre

4.1 Densidades

En principio, tenemos tanto densidades volumétricas como superficiales de carga libre

$\rho_l = \nabla\cdot\mathbf{D}$ $\sigma_l = \mathbf{n}\cdot[\mathbf{D}]$

Sin embargo, dado que el desplzamiento es uniforme en el interior de cada media, la densidad volumétrica de carga libre es nula

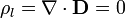
$\rho_l = \nabla\cdot\mathbf{D}=0$

Para la superficial, tenemos tres superficies: la de la placa inferior, la interfaz central y la superficie de la placa superior.

En la placa inferior: En la placa conductora, el campo eléctrico (y por tanto el desplazamiento) es nulo, así que

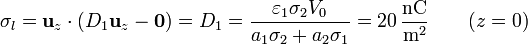
$\sigma_l = \mathbf{u}_z\cdot(D_1\mathbf{u}_z - \mathbf{0}) = D_1 = \frac{\varepsilon_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}= 20\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad (z=0)$

En la interfaz: en este caso, el desplazamiento es no nulo a un lado ya otro

$\sigma_l = \mathbf{u}_z\cdot(D_2\mathbf{u}_z - D_1\mathbf{u}_z) = D_2-D_1\frac{(\varepsilon_2\sigma_1-\varepsilon_1\sigma_2)V_0}{a_1\sigma_2+a_2\sigma_1}= 160\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad (z=a_1)$

En la placa superior: De nuevo, es nulo el campo en la placa conductora

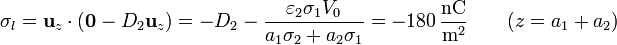
$\sigma_l = \mathbf{u}_z\cdot(\mathbf{0}-D_2\mathbf{u}_z) = - D_2 -\frac{\varepsilon_2\sigma_1V_0}{a_1\sigma_2+a_2\sigma_1}= -180\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad (z=a_1+a_2)$

4.2 Cargas

Una vez que tenemos las densidades de carga, es inmediato obtener la carga en cada superficie, por ser uniformes las densidades.

En la placa inferior: Integrando la densidad de carga superficial

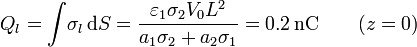
$Q_l = \int\! \sigma_l\,\mathrm{d}S = \frac{\varepsilon_1\sigma_2V_0L^2}{a_1\sigma_2+a_2\sigma_1}= 0.2\,\mathrm{nC}\qquad (z=0)$

Esta carga puede también hallarse mediante el flujo del vector desplazamiento a través de una superficie cerrada que envuelva a la placa inferior.
En la interfaz: Operando igualmente

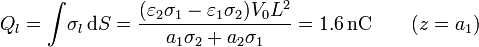
$Q_l = \int\! \sigma_l\,\mathrm{d}S = \frac{(\varepsilon_2\sigma_1-\varepsilon_1\sigma_2)V_0L^2}{a_1\sigma_2+a_2\sigma_1}= 1.6\,\mathrm{nC}\qquad (z=a_1)$

En la placa superior

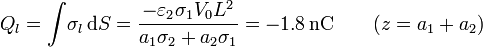
$Q_l = \int\! \sigma_l\,\mathrm{d}S = \frac{-\varepsilon_2\sigma_1V_0L^2}{a_1\sigma_2+a_2\sigma_1}= -1.8\,\mathrm{nC}\qquad (z=a_1+a_2)$

En el volumen no existe carga alguna, por ser nula la densidad de carga.

Podemos comprobar que el sistema es eléctricamente neutro

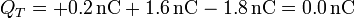
$Q_T = +0.2\,\mathrm{nC}+1.6\,\mathrm{nC}-1.8\,\mathrm{nC} = 0.0\,\mathrm{nC}$

5 Potencia y energía

5.1 Potencia

Podemos hallar la potencia total consumida en el sistema a partir de la densidad de potencia

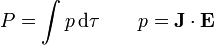
$P = \int p\,\mathrm{d}\tau\qquad p = \mathbf{J}\cdot\mathbf{E}$

Puesto que los campos son uniformes en cada material, tenemos dos valores de la densidad de potencia

En el medio 1

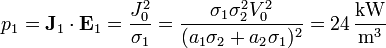
$p_1 = \mathbf{J}_1\cdot\mathbf{E}_1 = \frac{J_0^2}{\sigma_1} = \frac{\sigma_1\sigma_2^2V_0^2}{(a_1\sigma_2+a_2\sigma_1)^2} = 24\,\frac{\mathrm{kW}}{\mathrm{m}^3}$

En el medio 2

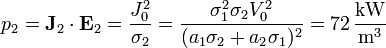
$p_2 = \mathbf{J}_2\cdot\mathbf{E}_2 = \frac{J_0^2}{\sigma_2} = \frac{\sigma_1^2\sigma_2V_0^2}{(a_1\sigma_2+a_2\sigma_1)^2} = 72\,\frac{\mathrm{kW}}{\mathrm{m}^3}$

La potencia total disipada es igual a

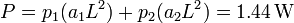
$P = p_1(a_1 L^2) + p_2(a_2L^2) = 1.44\,\mathrm{W}$

Esta potencia, por supuesto es igual a la que se obtiene si se halla empleando la expresión de teoría de circuitos

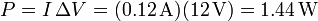
$P = I\,\Delta V = (0.12\,\mathrm{A})(12\,\mathrm{V}) = 1.44\,\mathrm{W}$

Más adelante veremos el análisis completo empleando teoría de circuitos.

6 Energía eléctrica

Igualmente, podemos hallar la energía almacenada integrando su densidad

$U_\mathrm{e} = \int u_\mathrm{e}\,\mathrm{d}\tau\qquad u_e = \frac{1}{2}\mathbf{E}\cdot\mathbf{D}=\frac{1}{2}\varepsilon E^2$

De nuevo tenemos dos valores, uno para cada región

En el medio 1

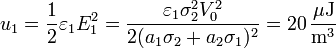
$u_1 = \frac{1}{2}\varepsilon_1 E_1^2 = \frac{\varepsilon_1\sigma_2^2V_0^2}{2(a_1\sigma_2+a_2\sigma_1)^2} = 20\,\frac{\mu\mathrm{J}}{\mathrm{m}^3}$

En el medio 2

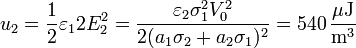
$u_2 = \frac{1}{2}\varepsilon_12 E_2^2 = \frac{\varepsilon_2\sigma_1^2V_0^2}{2(a_1\sigma_2+a_2\sigma_1)^2} = 540\,\frac{\mu\mathrm{J}}{\mathrm{m}^3}$

La energía total almacenada vale

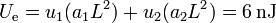
$U_\mathrm{e}=u_1(a_1 L^2) + u_2(a_2L^2) = 6\,\mathrm{nJ}$

Esta energía puede también calcularse a partir de la expresión para una densidad superficial de carga

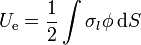
$U_\mathrm{e} = \frac{1}{2}\int \sigma_l\phi\,\mathrm{d}S$

Separando en las tres superficies y observando que cada una de ellas es equipotencial, queda

$U_\mathrm{e} = \frac{1}{2}Q(0)\overbrace{\phi(0)}^{=V_0} + \frac{1}{2}Q(a_1)\overbrace{\phi(a_1)}^{=V_1} + \frac{1}{2}Q(a_1+a_2)\overbrace{\phi(a_1+a_2)}^{=0}$

siendo $V 1$ el potencial de la interfaz, calculado anteriormente

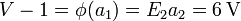
$V-1 = \phi(a_1) = E_2a_2 = 6\,\mathrm{V}$

Así llegamos de nuevo al mismo valor de la energía

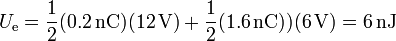
$U_\mathrm{e} = \frac{1}{2}(0.2\,\mathrm{nC})(12\,\mathrm{V})+\frac{1}{2}(1.6\,\mathrm{nC}))(6\,\mathrm{V})=6\,\mathrm{nJ}$

7 Solución mediante el circuito equivalente

7.1 Circuito equivalente

Todo el problema puede abordarse con ayuda de un circuito equivalente. Dado que la interfaz es paralela a las placas y equipotencial, este circuito está formado por dos asociaciones en serie, cada una representando a uno de los materiales. A su vez, cada material puede describirse como una resistencia en paralelo con un condensador.

Los valores de los capacidades del circuito son

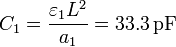
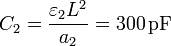
$C_1 = \frac{\varepsilon_1 L^2}{a_1}=33.3\,\mathrm{pF}$ $C_2 = \frac{\varepsilon_2 L^2}{a_2}=300\,\mathrm{pF}$

y los de las resistencias

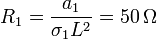
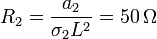
$R_1 = \frac{a_1}{\sigma_1 L^2}=50\,\Omega$ $R_2 = \frac{a_2}{\sigma_2 L^2}=50\,\Omega$

7.2 Tensión, carga y corriente

Al estar el sistema en un estado estacionario, los condensadores se encuentran cargados y por ellos no pasa corriente alguna. La única corriente fluye a través de las resistencias, que se encuentran en serie

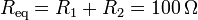
$R_\mathrm{eq} = R_1 + R_2 = 100\,\Omega$

La intensidad de corriente que atraviesa el circuito es entonces

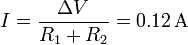
$I = \frac{\Delta V}{R_1 + R_2} = 0.12\,\mathrm{A}$

La tensión del nodo central vale

$V_1 - 0 = I R_2 = 6\,\mathrm{V}$

Una vez que tenemos la tensión de este nodo, podemos hallar la carga almacenada en cada condensador

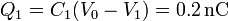
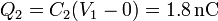
$Q_1 = C_1(V_0 - V_1) = 0.2\,\mathrm{nC}$ $Q_2 = C_2(V_1 - 0) = 1.8\,\mathrm{nC}$

Obsérvese que al ser las cargas diferentes, no puede considerarse que estos dos condensadores están en serie.

A partir de estos valores circuitales, podemos hallar las magnitudes que pide el problema, admitiendo de forma razonable, que el campo eléctrico, la densidad de corriente y el vector desplazamiento es uniforme en cada región.

7.3 Densidad de corriente

Si la corriente se distribuye uniformemente en cada sección

$\mathbf{J}_1 = \mathbf{J}_2 = \frac{I}{L^2}\mathbf{u}_z = 12\,\frac{\mathrm{A}}{\mathrm{m}^2}$

7.4 Campo eléctrico

En cada material el campo es igual a la diferencia de potencial dividida por la distancia entre superficies. En el medio inferior:

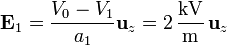
$\mathbf{E}_1 = \frac{V_0-V_1}{a_1}\mathbf{u}_z = 2\,\frac{\mathrm{kV}}{\mathrm{m}}\,\mathbf{u}_z$

y en el superior

$\mathbf{E}_2 = \frac{V_1-0}{a_2}\mathbf{u}_z = 6\,\frac{\mathrm{kV}}{\mathrm{m}}\,\mathbf{u}_z$

7.5 Vector desplazamiento

De la ley de Gauss resulta que el vector desplazamiento es igual a la carga libre dividida por el área de una sección. Esto nos da

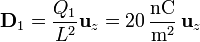
$\mathbf{D}_1 = \frac{Q_1}{L^2}\mathbf{u}_z = 20\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

y

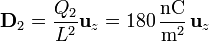
$\mathbf{D}_2 = \frac{Q_2}{L^2}\mathbf{u}_z = 180\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

7.6 Densidades y cargas libres

La carga libre en la placa inferior es la del primer condensador

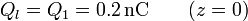
$Q_l = Q_1 = 0.2\,\mathrm{nC}\qquad (z=0)$

siendo su densidad

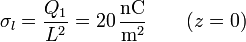
$\sigma_l = \frac{Q_1}{L^2}=20\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad(z=0)$

En la interfaz, la carga es la de la placa negativa del condensador 1 y la positiva del 2

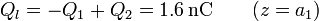
$Q_l = -Q_1 + Q_2 = 1.6\,\mathrm{nC}\qquad (z=a_1)$

con densidad

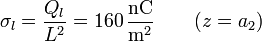
$\sigma_l = \frac{Q_l}{L^2}=160\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad(z=a_2)$

En la placa superior, es la negativa del condensador 2

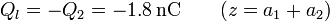
$Q_l = -Q_2 = -1.8\,\mathrm{nC}\qquad (z=a_1+a_2)$

con densidad

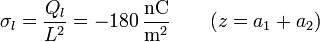
$\sigma_l = \frac{Q_l}{L^2}=-180\,\frac{\mathrm{nC}}{\mathrm{m}^2}\qquad(z=a_1+a_2)$

7.7 Potencia

La potencia disipada en el circito es la que se consume en las dos resistencias

$P = I^2 R_1 + I^2 R_2 = I^2 R_\mathrm{eq}=I V_0 = 1.44\,\mathrm{W}$

7.8 Energía almacenada

La energía electrostática es la almacenada en cada uno de los condensadores

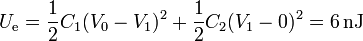
$U_\mathrm{e} = \frac{1}{2}C_1(V_0-V_1)^2 + \frac{1}{2}C_2(V_1-0)^2 = 6\,\mathrm{nJ}$

Vemos que hemos obtenido todos los valores pedidos. No obstante, una solución completa mediante el circuito equivalente requiere que se justifique primero que los campos son uniformes en cada uno de los materiales.