Comportamiento dieléctrico de la materia
De Laplace
Contenido |
1 Introducción
Todos los materiales permiten, en mayor o menor medida, el movimiento de cargas en su interior. Si se le aplica un campo eléctrico a un trozo de material tarde o temprano se llega al equilibrio electrostático. El periodo típico en que esto ocurre se denomina tiempo de relajación. Dependiendo de la duración del tiempo de relajación, los materiales pueden ordenarse, yendo desde los conductores muy buenos, como el cobre o la plata, con un tiempo de relajación muy corto (que se modelan como conductores perfectos hasta los que requieren periodos muy largos para alcanzar el equilibrio, como diversos plásticos o materiales orgánicos.
Para estos últimos materiales se emplea un modelo llamado dieléctrico ideal, que se caracteriza por no permitir en absoluto en flujo de carga por su interior. En este capítulo se consideran las propiedades de estos materiales. En el tema de corrientes eléctricas se estudia el comportamiento de dieléctricos no ideales.
2 Polarización
Los dieléctricos ideales afectan a los campos eléctricos porque aunque no fluyen y se redistribuyan las cargas en su interior, las moléculas y átomos que lo componen se polarizan, bien por la formación de dipolos inducidos, bien por la orientación de dipolos permanentes. Se define la polarización del material como la densidad de momento dipolar
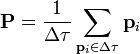
El potencial eléctrico debido a una polarización es la suma de los potenciales debidos a cada dipolo
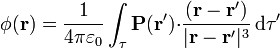
Esta integral suele ser difícil de calcular por métodos analíticos.
Una descripción alternativa es mediante las densidades de carga de polarización o de carga ligada, definidas como
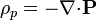
![\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]\,](/wiki/images/math/a/a/6/aa6172e549ca64c032e4c38ebbff7c6e.png)
La última fórmula, con el salto en la polarización, se aplica a una interfaz entre dos dieléctricos. Si uno de ellos es el vacío (en el
cual 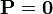 ), esta expresión se reduce a
), esta expresión se reduce a 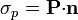 . En términos de ρp y σp el potencial es
. En términos de ρp y σp el potencial es
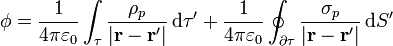
Empleando las cargas de polarización, las ecuaciones de la electrostática en presencia de dieléctricos se escriben como
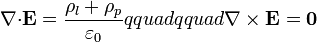
con las condiciones de salto
![\mathbf{n}{\cdot}[\mathbf{E}] = \frac{\sigma_l+\sigma_p}{\varepsilon_0}](/wiki/images/math/0/f/2/0f21e31dd3fd3bddd1df0ccafb74acab.png)
![\mathbf{n}\times
[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
siendo ρl y σl las densidades de carga libre, definidas como aquellas que no son de polarización.





