Problemas del segundo principio de la termodinámica
De Laplace
1 Ejemplo de máquina térmica
Una máquina térmica consume 240 kg de carbón por hora, siendo el poder calorífico de este combustible de 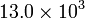 kcal/kg. Si la máquina tiene un rendimiento del 25% calcule el trabajo suministrado por la máquina y el calor cedido al foco frío en una hora
kcal/kg. Si la máquina tiene un rendimiento del 25% calcule el trabajo suministrado por la máquina y el calor cedido al foco frío en una hora
2 Rendimiento de un ciclo recorrido por un gas ideal
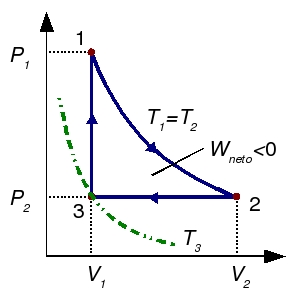
Un gas ideal diatómico recorre el siguiente ciclo: partiendo del el estado de coordenadas, 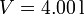 ,
, 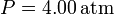 ,
, 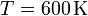 , se dilata isotérmicamente hasta duplicar su volumen. Después se comprime a presión constante hasta su volumen inicial. Finalmente se calienta a volumen constante hasta que alcanza la presión original. Calcule el rendimiento del ciclo.
, se dilata isotérmicamente hasta duplicar su volumen. Después se comprime a presión constante hasta su volumen inicial. Finalmente se calienta a volumen constante hasta que alcanza la presión original. Calcule el rendimiento del ciclo.
3 Sobrecoste originado por la luz de un frigorífico
El interruptor de la luz interior de un frigorífico está estropeado, de modo que la luz está siempre encendida. La luz interior consume una potencia de 40.0 W. Si la eficiencia del frigorífico es 1.3, y el coste de la electricidad es de 11.0 céntimos por kWh, calcule el incremento en el consumo del frigorífico y el coste añadido por año si no se arregla el interruptor.
4 Rendimiento de aparatos hipotéticos
Un inventor mantiene que ha desarrollado una máquina térmica que recibe 700 kJ de calor desde un foco térmico a 500 K y produce 300 kJ de trabajo neto transfiriendo el calor sobrante a un foco térmico a 290 K. ¿Es razonable?
Nuestro inventor vuelve a la carga, esta vez con un refrigerador que, asegura, mantiene el espacio refrigerado a 2°C mientras el ambiente se encuentra a 24°C, teniendo una eficiencia de 13.5. ¿Le hacemos caso?
5 Rendimiento de una máquina térmica real
Una máquina térmica que funciona entre 200°C y 80.0°C alcanza un 20.0% de su rendimiento teórico máximo. ¿Cuanta energía debe absorber para realizar 10.0 kJ de trabajo?
6 Ejemplo de frigorífico de Carnot
Una máquina frigorífica de las que se emplean para fabricar hielo funciona segín un ciclo de Carnot reversible absorbiendo calor de un tanque de agua a 0.00°C y cediéndolo al aire en el interior de un local que se mantiene a 26.0°C. La máquina fabrica 223 kg de hielo en un día. Calcule el trabajo consumido y el calor cedido al aire.
7 Ejemplo de bomba de calor de Carnot
Una bomba de calor se emplea para mantener caliente una vivienda que se encuentra a 20.0°C siendo la temperatura exterior -5.00°C. Suponiendo que la bomba de calor es una máquina de Carnot invertida, calcule cuantos julios de energía procedentes del medio ambiente exterior serán transferidos al interior de la vivienda por cada julio de energía eléctrica consumida. Explique las ventajas e incovenientes de este sistema de calefacción frente a uno convencional de disipación de energía en una resistencai eléctrica.
8 Producción de entropía en un frigorífico real
Para mantener su interior a 4°C en una habitación que se encuentra a 27°C un frigorífico ha de extraer 360 kJ/min de su interior. Si la entrada de potencia requerida por el frigorífico es 2 kW, determine:
- Eficiencia del refrigerador. Compárela con la eficiencia de un refrigerador ideal (reversible) que trabaje entre los mismos focos térmicos.
- Potencia extra que consume este frigorífico respecto a uno ideal que extraiga la misma energía de su interior.
- Entropía generada por segundo en el universo por la operación del frigorífico real.
9 Variación de entropía en el paso de hielo a vapor
Calcule la variación de entropía de un bloque de hielo de 27.0 g a −12.0°C cuando pasa reversiblemente al estado de vapor a 115°C, a presión constante.
Datos: cp (vapor) = 2.08 kJ/kg K, cp (agua) = 4.18 kJ/kg K, cp (hielo) = 2.11 kJ/kg K, Lf = 333.53 J/g, Lv=2257 J/g
10 Inmersión de un bloque metálico en agua
Un bloque de cobre de 50 kg a 80°C se deja caer en un tanque aislado adiabáticamente que contiene 120 l de agua a 25°C. Determine la temperatura final de equilibrio y la variación total del entropía.
Dato: cp(cobre) = 0.095 cal/g·K.
11 Variación de entropía con un baño térmico
Un tanque de volumen constante contiene 100 moles de aire a una presión de 100 kPa y una temperatura de 327°C. El aire se enfría hasta la temperatura del ambiente de 27.0°C. Suponiendo que el aire se comporta como un gas ideal diatómico, determine la variación de entropía del aire y del Universo durante el proceso.
12 Comparación de dos variaciones de entropía
Calcule la variación de entropía en las dos situaciones siguientes:
- 100 ml de agua a 80°C son vertidos en un tanque de agua a 20°C.
- 100 ml de agua a 20°C son vertidos en un tanque de agua a 80°C.
Suponga que la presión es la atmosférica en todo momento.
13 Ciclo con un proceso reversible y otro irreversible
Un mol de un gas ideal sufre en primer lugar una expansión libre desde 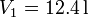 y
y
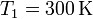 hasta
hasta 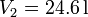 y
y 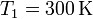 .
Luego se comprime isoterma y cuasiestáticamente, volviendo a sus estado original.
.
Luego se comprime isoterma y cuasiestáticamente, volviendo a sus estado original.
- ¿Cuál es la variación de entropía del Universo en el ciclo completo?
- ¿Cuanto trabajo se desperdicia en este ciclo?
- Demuestre que este trabajo perdido es TΔSu.
14 Entropía de una mezcla de gases
Un recipiente de 2.00 l tiene una barrera que lo divide por la mitad. Una mitad contiene H2 y la otra O2. Ambos gases se encuentran a temperatura ambiente y presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?
15 Máximo aprovechamiento del calor
Suponga que se tiene un bloque de 10 kg de hierro (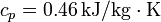 ) a una temperatura de 200°C y se quiere usar para caldear una gran habitación a una temperatura
) a una temperatura de 200°C y se quiere usar para caldear una gran habitación a una temperatura 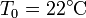 , estando el exterior a 5°C.
, estando el exterior a 5°C.
- Si se coloca el bloque directamente en la habitación, calcule el calor que libera al ambiente.
- Halle la variación de entropía del bloque y del universo en el caso anterior.
- El calor del bloque puede aprovecharse para producir algún trabajo. Para ello, suponga que cuando el bloque se encuentra a una temperatura T, y libera una cantidad de calor
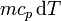 , dicho calor se hace pasar por una máquina reversible que opera entre la temperatura T y la del ambiente. Calcule el trabajo obtenible en este paso y la cantitad total de trabajo que se podría obtener.
, dicho calor se hace pasar por una máquina reversible que opera entre la temperatura T y la del ambiente. Calcule el trabajo obtenible en este paso y la cantitad total de trabajo que se podría obtener.
- Compruebe que el trabajo perdido es igual a T0ΔSu
- Si ese trabajo se aprovechara para hacer funcionar una bomba de calor reversible que operara entre el exterior y la habitación, ¿cuánto sería el calor total que se liberaría en la habitación?
16 Exergía de un volumen de aire comprimido en un tanque
Un tanque de 200 m3 de volumen contiene aire a una presión de 1 MPa y temperatura de 300 K. Determine que cantidad máxima de trabajo puede obtenerse de él si las condiciones del entorno son P0=100 kPa y T0=300 K.
17 Eficiencia de un ciclo Otto
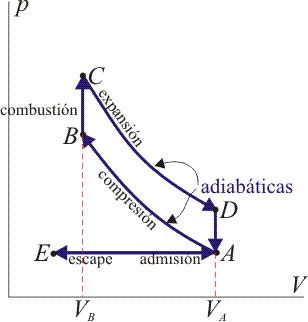
Un ciclo Otto ideal modela el comportamiento de un motor de explosión. Este ciclo está formado por seis pasos, según seindica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión
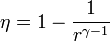
siendo r = VA / VB la razón de compresión. Para ello, halle el rendimiento a partir del calor que entra en el sistema y el que sale de él; exprese el resultado en términos de las temperaturas en los vértices del ciclo y, con ayuda de la ley de Poisson, relacione este resultado con los volúmenes VA y VB.
18 Caso práctico de ciclo Otto
Suponga un ciclo Otto ideal con una relación de compresión de 8. Al inicio de la fase de compresión, el aire está a 100 kPa y 17°C. En la combustión se añaden 800 kJ/kg de calor. Determine la temperatura y la presión máximas que se producen en el ciclo, la salida de trabajo neto y el rendimiento de este motor.
19 Eficiencia de un ciclo Brayton
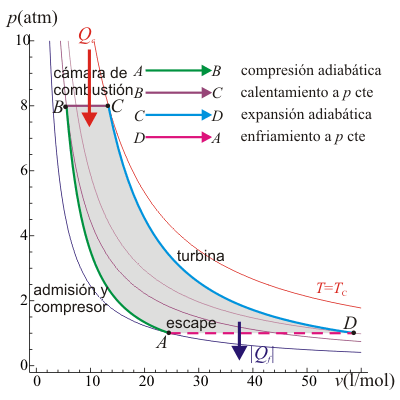
Un ciclo Brayton (o Joule) ideal modela el comportamiento de una turbina, como las empleadas en las aeronaves. Este ciclo está formado por cuatro pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión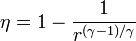
siendo r = p2 / p1 la relación de presión. El método para obtener este resultado es análogo al empleado para el ciclo Otto.
20 Caso práctico de ciclo Brayton
Una central eléctrica de turbina de gas que opera en un ciclo Brayton ideal tiene una relación de presión de 8. La temperatura del gas es de 300 K en la entrada del compresor y de 1300 K en la entrada de la turbina. Determine la temperatura del gas a la salida del compresor y de la turbina, y la eficiencia de esta turbina.