Electrostática en presencia de conductores
De Laplace
(→Problema del potencial) |
(→Propiedades de los conductores en equilibrio) |
||
| (31 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Equilibrio electrostático== | ==Equilibrio electrostático== | ||
| - | + | {{ac|Equilibrio electrostático}} | |
La propiedad definitoria de un material conductor es que permite el movimiento de las cargas en su interior. Cuando un conductor se ve sometido a un campo eléctrico, las cargas se redistribuyen hasta que se alcanza el ''equilibrio electrostático'', en el cual las cargas se encuentran en reposo. | La propiedad definitoria de un material conductor es que permite el movimiento de las cargas en su interior. Cuando un conductor se ve sometido a un campo eléctrico, las cargas se redistribuyen hasta que se alcanza el ''equilibrio electrostático'', en el cual las cargas se encuentran en reposo. | ||
| Línea 9: | Línea 9: | ||
==Propiedades de los conductores en equilibrio== | ==Propiedades de los conductores en equilibrio== | ||
| - | + | {{ac|Consecuencias del equilibrio electrostático}} | |
Como consecuencia de la condición de equilibrio electrostático | Como consecuencia de la condición de equilibrio electrostático | ||
| + | * El campo eléctrico es nulo en el material conductor | ||
* El material conductor es equipotencial. | * El material conductor es equipotencial. | ||
* No hay densidad de carga de volumen en el material. | * No hay densidad de carga de volumen en el material. | ||
* Toda la carga está almacenada en las superficies del conductor. | * Toda la carga está almacenada en las superficies del conductor. | ||
* No hay líneas de campo que vayan de un conductor a él mismo. | * No hay líneas de campo que vayan de un conductor a él mismo. | ||
| - | * El campo justo | + | * El campo justo fuera del conductor es perpendicular a la superficie. |
| + | * El campo justo fuera del conductor es de la forma | ||
<center><math>\mathbf{E} = \frac{\sigma_s}{\varepsilon_0}\mathbf{n}</math></center> | <center><math>\mathbf{E} = \frac{\sigma_s}{\varepsilon_0}\mathbf{n}</math></center> | ||
| Línea 24: | Línea 26: | ||
{{ac|Problema del potencial}} | {{ac|Problema del potencial}} | ||
| - | Si tenemos un conjunto de conductores cuya carga o cuyo potencial es | + | Si tenemos un conjunto de conductores cuya carga o cuyo potencial es conocido, además de una cierta distribución de carga volumétrica en el espacio entre ellos, el problema del potencial consiste en resolver la ecuación de Poisson |
| - | conocido, además de una cierta distribución de carga volumétrica en el | + | |
| - | espacio entre ellos, el problema del potencial consiste en resolver la | + | |
| - | ecuación de Poisson | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | La solución del problema del potencial puede escribirse como una | + | <center><math>\nabla^2\phi = -\frac{\rho}{\varepsilon_0}</math></center> |
| - | superposición | + | |
| - | + | en el espacio <math>\tau</math> entre los conductores, con las condiciones de contorno | |
| - | \phi = \phi_0 + \ | + | |
| - | \ | + | <center><math>\phi = V_i\,</math>{{qquad}}<math>(\mathbf{r}\in S_i)</math></center> |
| - | siendo | + | |
| + | siendo <math>S_i</math> la superficie del conductor <math>i</math>. Para aquellos conductores cuyo potencial no se conozca, sus valores pueden obtenerse de las condiciones | ||
| + | |||
| + | <center><math>Q_i = \varepsilon_0\oint_{S_i} \mathbf{E}{\cdot}\mathrm{d}\mathbf{S}_i = -\varepsilon_0\oint_{S_i} \nabla\phi{\cdot}\mathrm{d}\mathbf{S}_i</math></center> | ||
| + | |||
| + | siendo <math>S_i</math> una superficie que envuelve al conductor <math>i</math>. | ||
| + | |||
| + | La solución del problema del potencial puede escribirse como una superposición | ||
| + | |||
| + | <center><math>\phi = \phi_0 + \sum_k V_k\phi_k\,</math></center> | ||
| + | |||
| + | siendo <math>\phi_0</math> el potencial que habría si la densidad de carga | ||
estuviera presente pero los conductores estuvieran a tierra | estuviera presente pero los conductores estuvieran a tierra | ||
| - | + | ||
| - | \nabla^2\phi_0 = -\frac{\rho}{\ | + | <center><math>\nabla^2\phi_0 = -\frac{\rho}{\varepsilon_0}</math>{{qquad}}<math>(\mathbf{r}\in\tau)</math>{{qquad}}{{qquad}}<math>\phi_0=0</math>{{qquad}}<math>(\mathbf{r}\in S_i)</math></center> |
| - | \phi_0=0\ | + | |
| - | \ | + | y <math>\phi_k</math> es el potencial supuesto que el conductor <math>k</math> está a potencial unidad y el resto a tierra |
| - | y | + | |
| - | potencial unidad y el resto a tierra | + | <center><math>\nabla^2\phi_k=0</math>{{qquad}}<math>(\mathbf{r}\in\tau)</math>{{qquad}} |
| - | + | <math>\phi_k = 1\,</math>{{qquad}}<math>(\mathbf{r}\in S_k)</math>{{qquad}}<math>\phi_k=0\,</math>{{qquad}} <math>(\mathbf{r}\in S_i\quad i\neq k)</math></center> | |
| - | \nabla^2\ | + | |
| - | \ | + | |
| - | + | ||
| - | + | ||
==Coeficientes de capacidad== | ==Coeficientes de capacidad== | ||
| + | {{ac|Coeficientes de capacidad}} | ||
| + | |||
| + | Si no hay densidad de carga volumétrica, las cargas almacenadas en los distintos conductores forman una combinación lineal de los potenciales respectivos | ||
| + | |||
| + | <center><math>Q_i = \sum_j C_{ik}V_k\,</math></center> | ||
| + | |||
| + | siendo los <math>C_{ik}</math> los ''coeficientes de capacidad''. | ||
| + | |||
| + | Estas relaciones pueden expresarse en forma matricial | ||
| + | |||
| + | <center><math>\mathbf{Q}=\mathbf{\mathsf{C}}{\cdot}\mathbf{V}</math></center> | ||
| + | |||
| + | siendo <math>\mathbf{Q}</math> y <math>\mathbf{V}</math> dos vectores columna y <math>\mathbf{\mathsf{C}}</math> una matriz cuadrada simétrica y definida positiva. | ||
| + | |||
| + | Los coeficientes de capacidad verifican | ||
| + | |||
| + | <center><math>C_{ii}> 0\,</math>{{qquad}}<math>C_{ik}\leq 0</math>{{qquad}}<math>(i\neq k)</math></center> | ||
| + | |||
| + | ===Capacidad de un conductor=== | ||
| + | {{ac|Capacidad de un conductor}} | ||
| + | |||
| + | En el caso particular de un solo ''conductor'', la expresión se reduce a | ||
| + | |||
| + | <center><math>Q = C V\,</math></center> | ||
| + | |||
| + | con <math>C</math> la ''capacidad del conductor'', medida en faradios (F). Como | ||
| + | caso particular, para una esfera de radio <math>R</math> | ||
| + | |||
| + | <center><math>C = 4\pi\varepsilon_0 R</math></center> | ||
| + | |||
==Condensadores y circuitos equivalentes== | ==Condensadores y circuitos equivalentes== | ||
| + | ===Capacidad de un condensador=== | ||
| + | {{ac|Capacidad de un condensador}} | ||
| + | |||
| + | Dos superficies conductoras están en [[influencia total]] si todas las líneas de campo que parten de una van a parar a la otra, para valores arbitrarios de los potenciales. En este caso, las superficies forman un \emph{condensador}. La carga almacenada en cada una cumple | ||
| + | |||
| + | <center><math>Q_1 = C(V_1-V_2)\,</math>{{qquad}}{{qquad}}<math>Q_2 = C(V_2-V_1)=-Q_1\,</math></center> | ||
| + | |||
| + | siendo <math>C</math> la ''capacidad del condensador''. Como casos particulares | ||
| + | tenemos el condensador de placas planas y paralelas, el condensador cilíndrico coaxial de radios <math>a</math> y <math>b</math> y el condensador esférico de radios <math>a</math> y <math>b</math>, con capacidades respectivas | ||
| + | |||
| + | <center><math>C_\mathrm{plano} = \frac{\varepsilon_0 S}{a}</math>{{qquad}}{{qquad}}<math>C_\mathrm{cil}=\frac{2\pi\varepsilon_0 L}{\ln(b/a)}</math>{{qquad}}{{qquad}}<math>C_\mathrm{esf}=\frac{4\pi\varepsilon_0 a b}{b-a}</math></center> | ||
| + | |||
| + | Para otros sistemas deberá resolverse la ecuación de Laplace en el espacio entre las superficies, con las condiciones de que en una de ellas el potencial valga <math>V</math> y en la otra sea nulo, y calcular la carga en la placa a mayor tensión. | ||
| + | |||
| + | ===Circuitos equivalentes=== | ||
| + | {{ac|Circuito equivalente a un sistema de conductores}} | ||
| + | |||
| + | Todo sistema de <math>N</math> conductores en equilibrio puede modelarse por un | ||
| + | circuito equivalente de <math>N(N+1)/2</math> condensadores. Cada conductor es representado por un nodo del circuito. Entre cada dos nodos existe un condensador de capacidad | ||
| + | |||
| + | <center><math>\overline{C}_{ik}= -C_{ij}</math>{{qquad}}<math>(i\neq k)\,</math></center> | ||
| + | |||
| + | Este condensador estará ausente si los conductores <math>k</math> e <math>i</math> están apantallados por algún otro y no son conectados por ninguna línea de campo. | ||
| + | |||
| + | Además, para representar aquellas líneas de campo que pueden ir de cada conductor hasta el infinito, existen <math>N</math> condensadores adicionales, | ||
| + | cada uno situado entre un nodo y tierra. La capacidad (''autocapacidad'') del condensador conectado al nodo <math>i</math> vale | ||
| + | |||
| + | <center><math>\overline{C}_{ii} = \sum_{j=1}^N C_{ik}</math></center> | ||
| + | |||
| + | Conocida la matriz de los coeficientes de capacidad pueden calcularse | ||
| + | las <math>N(N-1)/2</math> capacidades y las <math>N</math> autocapacidades, y viceversa. | ||
| + | |||
| + | Además de estos condensadores, habrá que incluir una fuente de tensión continua conectada a cada nodo cuyo potencial esté fijado. Si la cantidad fijada es la carga del conductor, debe suponerse conectada a un “generador de carga”, que simplemente expresaría que la carga total almacenada en todos los condensadores conectados a dicho nodo es un valor dado y no nula. Si el elemento está aislado y descargado (<math>Q=0</math> y potencial desconocido) este elemento puede suprimirse. | ||
| + | |||
==Método de las imágenes== | ==Método de las imágenes== | ||
==Métodos numéricos== | ==Métodos numéricos== | ||
==Energía de un sistema de conductores== | ==Energía de un sistema de conductores== | ||
| + | {{ac|Energía de un sistema de conductores}} | ||
| + | |||
| + | Dado un sistema de <math>N</math> conductores, sin carga entre ellos, la energía almacenada en el sistema puede expresarse como | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\sum_i Q_i V_i =\frac{1}{2}\sum_{ik} | ||
| + | C_{ik}V_iV_k</math></center> | ||
| + | |||
| + | Si además de los conductores tenemos cargas de volumen o puntuales en el espacio entre ellos, habrá que añadir los correspondientes términos | ||
| + | |||
| + | <center><math>U_\mathrm{e} =\frac{1}{2}\sum_iQ_i V_i + \frac{1}{2}\int\!\! | ||
| + | \rho\,\phi\,\mathrm{d}\tau + \frac{1}{2}\sum_n q_n\phi'(\mathbf{r}_n)</math></center> | ||
| + | |||
| + | donde <math>\phi</math> es el potencial total en cada punto y <math>\phi'</math> es el potencial total exceptuando la contribución debida a la propia carga puntual. | ||
| + | |||
==Presión sobre la superficie de los conductores== | ==Presión sobre la superficie de los conductores== | ||
| + | {{ac|Presión electrostática}} | ||
| + | |||
| + | El cálculo de las fuerzas entre conductores puede realizarse a partir de la presión electrostática sobre ellos. Debido a la repulsión | ||
| + | eléctrica, en cada punto de la superficie del conductor existe una presión dada por | ||
| + | |||
| + | <center><math>p=\frac{1}{2}\varepsilon E^2 = \frac{\sigma_s^2}{2\varepsilon}</math></center> | ||
| + | |||
| + | siendo la fuerza elemental sobre cada punto de la superficie | ||
| + | |||
| + | <center><math>\mathrm{d}\mathbf{F} = p\,\mathrm{d}\mathbf{S} = \frac{1}{2}\varepsilon E^2\,\mathrm{d}S\,\mathbf{n}</math></center> | ||
| + | |||
| + | esto es, siempre normal y hacia afuera del conductor. | ||
| + | |||
==Fuerzas entre conductores== | ==Fuerzas entre conductores== | ||
==Problemas== | ==Problemas== | ||
| - | + | {{ac|Problemas de campo eléctrico en presencia de conductores}} | |
| - | + | <categorytree mode=pages depth="2">Problemas de electrostática en presencia de conductores</categorytree> | |
| - | [[Categoría: | + | [[Categoría:Electrostática en presencia de conductores|0]] |
| + | [[Categoría:Electrostática|20]] | ||
| + | [[Categoría:Campos Electromagnéticos|30]] | ||
última version al 11:06 8 mar 2011
1 Equilibrio electrostático
La propiedad definitoria de un material conductor es que permite el movimiento de las cargas en su interior. Cuando un conductor se ve sometido a un campo eléctrico, las cargas se redistribuyen hasta que se alcanza el equilibrio electrostático, en el cual las cargas se encuentran en reposo.
La condición de reposo implica que la fuerza neta sobre cada carga es nula. Puesto que la fuerza sobre las cargas en reposo es una fuerza eléctrica, la condición de equilibrio implica que en el material conductor
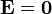
2 Propiedades de los conductores en equilibrio
Como consecuencia de la condición de equilibrio electrostático
- El campo eléctrico es nulo en el material conductor
- El material conductor es equipotencial.
- No hay densidad de carga de volumen en el material.
- Toda la carga está almacenada en las superficies del conductor.
- No hay líneas de campo que vayan de un conductor a él mismo.
- El campo justo fuera del conductor es perpendicular a la superficie.
- El campo justo fuera del conductor es de la forma
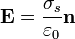
3 Problema del potencial
Si tenemos un conjunto de conductores cuya carga o cuyo potencial es conocido, además de una cierta distribución de carga volumétrica en el espacio entre ellos, el problema del potencial consiste en resolver la ecuación de Poisson
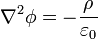
en el espacio τ entre los conductores, con las condiciones de contorno
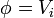
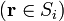
siendo Si la superficie del conductor i. Para aquellos conductores cuyo potencial no se conozca, sus valores pueden obtenerse de las condiciones
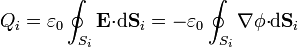
siendo Si una superficie que envuelve al conductor i.
La solución del problema del potencial puede escribirse como una superposición
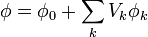
siendo φ0 el potencial que habría si la densidad de carga estuviera presente pero los conductores estuvieran a tierra
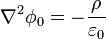
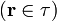 φ0 = 0
φ0 = 0 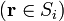
y φk es el potencial supuesto que el conductor k está a potencial unidad y el resto a tierra
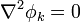
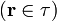
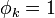
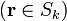
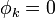
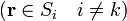
4 Coeficientes de capacidad
Si no hay densidad de carga volumétrica, las cargas almacenadas en los distintos conductores forman una combinación lineal de los potenciales respectivos
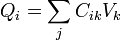
siendo los Cik los coeficientes de capacidad.
Estas relaciones pueden expresarse en forma matricial
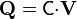
siendo 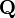 y
y 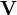 dos vectores columna y
dos vectores columna y 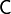 una matriz cuadrada simétrica y definida positiva.
una matriz cuadrada simétrica y definida positiva.
Los coeficientes de capacidad verifican
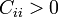
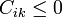
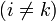
4.1 Capacidad de un conductor
En el caso particular de un solo conductor, la expresión se reduce a
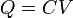
con C la capacidad del conductor, medida en faradios (F). Como caso particular, para una esfera de radio R
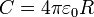
5 Condensadores y circuitos equivalentes
5.1 Capacidad de un condensador
Dos superficies conductoras están en influencia total si todas las líneas de campo que parten de una van a parar a la otra, para valores arbitrarios de los potenciales. En este caso, las superficies forman un \emph{condensador}. La carga almacenada en cada una cumple
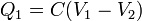
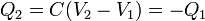
siendo C la capacidad del condensador. Como casos particulares tenemos el condensador de placas planas y paralelas, el condensador cilíndrico coaxial de radios a y b y el condensador esférico de radios a y b, con capacidades respectivas
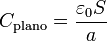
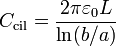
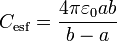
Para otros sistemas deberá resolverse la ecuación de Laplace en el espacio entre las superficies, con las condiciones de que en una de ellas el potencial valga V y en la otra sea nulo, y calcular la carga en la placa a mayor tensión.
5.2 Circuitos equivalentes
Todo sistema de N conductores en equilibrio puede modelarse por un circuito equivalente de N(N + 1) / 2 condensadores. Cada conductor es representado por un nodo del circuito. Entre cada dos nodos existe un condensador de capacidad
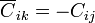
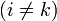
Este condensador estará ausente si los conductores k e i están apantallados por algún otro y no son conectados por ninguna línea de campo.
Además, para representar aquellas líneas de campo que pueden ir de cada conductor hasta el infinito, existen N condensadores adicionales, cada uno situado entre un nodo y tierra. La capacidad (autocapacidad) del condensador conectado al nodo i vale
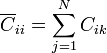
Conocida la matriz de los coeficientes de capacidad pueden calcularse las N(N − 1) / 2 capacidades y las N autocapacidades, y viceversa.
Además de estos condensadores, habrá que incluir una fuente de tensión continua conectada a cada nodo cuyo potencial esté fijado. Si la cantidad fijada es la carga del conductor, debe suponerse conectada a un “generador de carga”, que simplemente expresaría que la carga total almacenada en todos los condensadores conectados a dicho nodo es un valor dado y no nula. Si el elemento está aislado y descargado (Q = 0 y potencial desconocido) este elemento puede suprimirse.
6 Método de las imágenes
7 Métodos numéricos
8 Energía de un sistema de conductores
Dado un sistema de N conductores, sin carga entre ellos, la energía almacenada en el sistema puede expresarse como
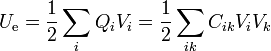
Si además de los conductores tenemos cargas de volumen o puntuales en el espacio entre ellos, habrá que añadir los correspondientes términos
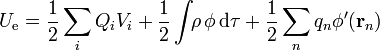
donde φ es el potencial total en cada punto y φ' es el potencial total exceptuando la contribución debida a la propia carga puntual.
9 Presión sobre la superficie de los conductores
El cálculo de las fuerzas entre conductores puede realizarse a partir de la presión electrostática sobre ellos. Debido a la repulsión eléctrica, en cada punto de la superficie del conductor existe una presión dada por
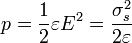
siendo la fuerza elemental sobre cada punto de la superficie
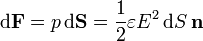
esto es, siempre normal y hacia afuera del conductor.





