Cinco planos conductores

De Laplace

Contenido

1 Enunciado
2 Coeficientes de capacidad
3 Cargas y tensiones
4 Energía electrostática
5 Campo eléctrico
6 Conexión a tierra

1 Enunciado

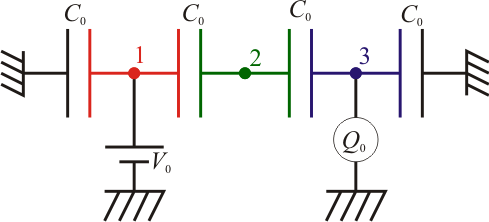
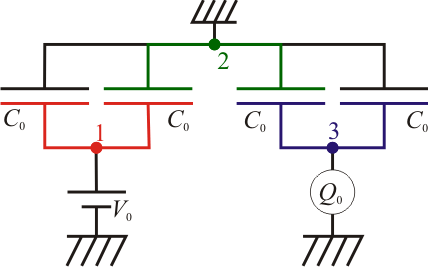
Cinco placas cuadradas de lado

L

, conductoras, se encuentran en la disposición indicada en la figura. La distancia entre cada par de placas paralelas es

a

( $a\ll L$ ).

Las dos placas exteriores se encuentran permanentemente a tierra, de forma que funcionan como referencia de potencial.

En todo momento, la segunda placa se encuentra puesta a potencial $V 0$ mientras que la cuarta almacena una carga $Q 0$ . La placa central se encuentra aislada y descargada.

Considerando el sistema de 3 conductores formado por las tres placas intermedias, halle la matriz de coeficientes de capacidad,
Halle la carga almacenada en cada una de las cinco placas cuadradas, así como la tensión de cada una.
Calcule la energía electrostática del sistema.
Calcule el valor del campo eléctrico en cada uno de los condensadores que se forman.
Si la placa central se conecta a tierra, ¿cómo cambian las cargas, los voltajes y la energía almacenada?

Desprecie los efectos de borde.

2 Coeficientes de capacidad

El sistema se compone de tres conductores vivos (en el sentido de que sus tensiones se pueden variar) más los dos exteriores, que actúan como la tierra del sistema. Esto es, no se trata de que haya que actuar como si las dos placas exteriores no estuvieran, sino que éstas desempeñan el papel que en otros sistemas (como los de dos esferas) le corresponde al infinito.

Tenemos el sistema de tres conductores, que se puede modelar por un circuito equivalente con tres nodos y, en principio, seis condensadores (tres entre los nodos y tres con tierra). Sin embargo, es evidente que nos bastan solo cuatro condensadores, los que forman cada para de placas consecutivas. Puesto que no hay líneas de campo que vayan de la placa 1 a la 3, ni de la 2 a tierra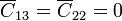 $\overline{C}_{13}=\overline{C}_{22}=0$

La capacidad de cada uno de estos condensadores es igual en todos los casos a

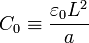
$C_0 \equiv \frac{\varepsilon_0L^2}{a}$

Las capacidades del circuito equivalente son entonces

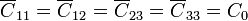
$\overline{C}_{11}=\overline{C}_{12}=\overline{C}_{23}=\overline{C}_{33}=C_0$

A partir de aquí obtenemos los coeficientes de capacidad

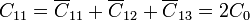
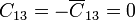
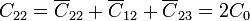
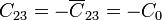
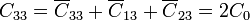
$C_{11}=\overline{C}_{11}+\overline{C}_{12} +\overline{C}_{13}=2C_0$ $C_{12}=-\overline{C}_{12}=-C_0$ $C_{13}=-\overline{C}_{13}=0$ $C_{22}=\overline{C}_{22}+\overline{C}_{12} +\overline{C}_{23}=2C_0$ $C_{23}=-\overline{C}_{23}=-C_0$ $C_{33}=\overline{C}_{33}+\overline{C}_{13} +\overline{C}_{23}=2C_0$

siendo el resto simétricos a éstos.

En forma matricial

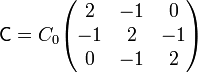
$\mathsf{C}=C_0\begin{pmatrix}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{pmatrix}$

Esta matriz cumple, como era de esperar, que es simétrica, que los términos de la diagonal principal son estrictamente positivos y que los no diagonales son negativos o nulos.

A este resultado se puede llegar de forma quizás más intuitiva a partir de las relaciones entre las cargas y las tensiones. La carga en cada una de las placas es la suma de las que hay en cada cara. A su vez, éstas son las cargas de placas de condensadores planos. Por tanto

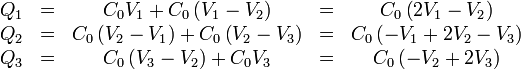
$\begin{matrix}Q_1 & = & C_0 V_1 + C_0\left(V_1 - V_2\right) & = & C_0\left(2V_1-V_2\right)\\Q_2 & = & C_0\left(V_2-V_1\right) + C_0\left(V_2 - V_3\right) & = & C_0\left(-V_1+2V_2-V_3\right)\\Q_3 &= &C_0\left(V_3-V_2\right) + C_0V_3 &= &C_0\left(-V_2+2V_3\right)\end{matrix}$

y, en forma matricial, queda

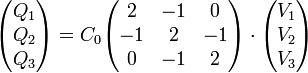
$\begin{pmatrix}Q_1\\Q_2\\Q_3\end{pmatrix} = C_0\begin{pmatrix}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{pmatrix}\cdot\begin{pmatrix}V_1\\V_2\\V_3\end{pmatrix}$

3 Cargas y tensiones

El cálculo del apartado anterior es completamente general en cuanto a los valores de las tensiones y las cargas. No hace falta usar para nada los valores del caso concreto del enunciado. Estos valores se usarán ahora, cuando se trata de aplicar las ecuaciones anteriores a un caso particular.

Nuestros datos son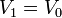 $V_1 = V_0\,$ $Q_2 = 0\,$ $Q_3 = Q_0\,$

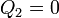
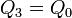
Nótese que de la placa central, por estar aislada y descargada, lo que conocemos es su carga (nula), no su tensión. En términos del circuito equivalente, esto corresponde a conectar una fuente de tensión $V 0$ al nodo 1 y una de carga $Q 0$ al 3. Al nodo 2 no hace falta conectar nada.

Sustituyendo esto en el sistema de ecuaciones

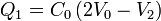
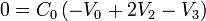
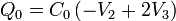
$Q_1 = C_0\left(2V_0-V_2\right)$ $0 = C_0\left(-V_0+2V_2-V_3\right)$ $Q_0 = C_0\left(-V_2+2V_3\right)$

Resolviendo para $V 2$

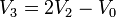
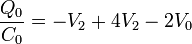
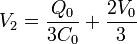
$V_3 = 2V_2-V_0\,$ $\frac{Q_0}{C_0}=-V_2+4V_2-2V_0$ $\Rightarrow$ $V_2 = \frac{Q_0}{3C_0}+\frac{2V_0}{3}$

y de aquí hallamos $Q 1$ y $V 3$

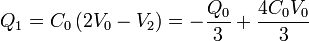
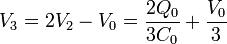
$Q_1 = C_0\left(2V_0-V_2\right) = -\frac{Q_0}{3}+\frac{4C_0V_0}{3}$ $V_3 = 2V_2-V_0 = \frac{2Q_0}{3C_0}+\frac{V_0}{3}$

Reuniendo todos los resultados

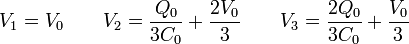
$V_1 = V_0\qquad V_2 = \frac{Q_0}{3C_0}+\frac{2V_0}{3}\qquad V_3 = \frac{2Q_0}{3C_0}+\frac{V_0}{3}$ $Q_1 = -\frac{Q_0}{3}+\frac{4C_0V_0}{3}\qquad Q_2 = 0 \qquad Q_3 = Q_0$

En forma matricial

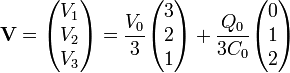
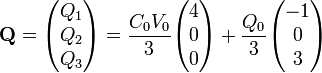
$\mathbf{V}=\begin{pmatrix}V_1\\ V_2\\V_3\end{pmatrix}=\frac{V_0}{3}\begin{pmatrix}3\\2\\1\end{pmatrix}+\frac{Q_0}{3C_0}\begin{pmatrix} 0 \\ 1 \\ 2\end{pmatrix}$ $\mathbf{Q}=\begin{pmatrix}Q_1\\ Q_2\\Q_3\end{pmatrix}=\frac{C_0V_0}{3}\begin{pmatrix}4\\0\\0\end{pmatrix}+\frac{Q_0}{3}\begin{pmatrix} -1 \\ 0 \\ 3\end{pmatrix}$

Nos queda por hallar las cargas de las placas exteriores. Estas las calculamos observando que se tratan de las placas de sendos condensadores.

Para la situada junto al conductor 1

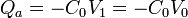
$Q_a = -C_0V_1 = -C_0V_0\,$

y para la situada junto al 3

$Q_b = -C_0V_3 = -\frac{2Q_0}{3}-\frac{C_0V_0}{3}$

Puede observarse que la suma de las cinco cargas es nula

$Q_a+Q_1+Q_2+Q_3+Q_b = -C_0V_0-\frac{Q_0}{3}+\frac{4C_0V_0}{3}+0+Q_0-\frac{2Q_0}{3}-\frac{C_0V_0}{3}=0$

como corresponde a que el campo en el exterior del sistema es nulo (y por tanto, según la ley de Gauss, también lo es la carga encerrada).

4 Energía electrostática

Una vez que tenemos las cargas y tensiones, podemos calcular la energía almacenada a partir del sumatorio

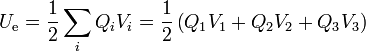
$U_\mathrm{e}=\frac{1}{2}\sum_iQ_iV_i = \frac{1}{2}\left(Q_1V_1+Q_2V_2+Q_3V_3\right)$

Sustituyendo los valores que hemos calculado

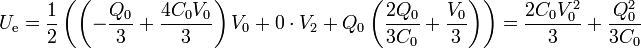
$U_\mathrm{e}= \frac{1}{2}\left(\left(-\frac{Q_0}{3}+\frac{4C_0V_0}{3}\right)V_0+0\cdot V_2+Q_0\left(\frac{2Q_0}{3C_0}+\frac{V_0}{3}\right)\right) = \frac{2C_0V_0^2}{3}+\frac{Q_0^2}{3C_0}$

Esta misma energía también se puede calcular como suma de las almacenadas en cada uno de los condensadores que forman el sistema

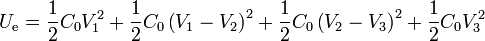
$U_\mathrm{e}=\frac{1}{2}C_0V_1^2 +\frac{1}{2}C_0\left(V_1-V_2\right)^2+\frac{1}{2}C_0\left(V_2-V_3\right)^2+\frac{1}{2}C_0V_3^2$

Las diferencias de potencial en cada condensador valen

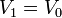
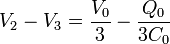
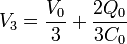
$V_1 = V_0\,$ $V_1-V_2=\frac{V_0}{3}-\frac{Q_0}{3C_0}$ $V_2-V_3 = \frac{V_0}{3}-\frac{Q_0}{3C_0}$ $V_3 = \frac{V_0}{3}+\frac{2Q_0}{3C_0}$

La energía de cada uno

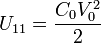
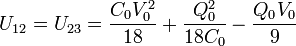
$U_{11} = \frac{C_0V_0^2}{2}$ $U_{12} = U_{23} = \frac{C_0V_0^2}{18}+\frac{Q_0^2}{18C_0}-\frac{Q_0V_0}{9}$ $U_{33}=\frac{C_0V_0^2}{18}+\frac{4Q_0^2}{18C_0}+\frac{2Q_0V_0}{9}$

y, sumándolo todo,

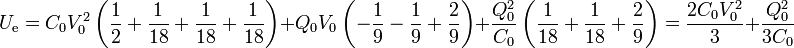
$U_\mathrm{e}=C_0V_0^2\left(\frac{1}{2}+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}\right)+Q_0V_0\left(-\frac{1}{9}-\frac{1}{9}+\frac{2}{9}\right)+\frac{Q_0^2}{C_0}\left(\frac{1}{18}+\frac{1}{18}+\frac{2}{9}\right)=\frac{2C_0V_0^2}{3}+\frac{Q_0^2}{3C_0}$

5 Campo eléctrico

Cuando se desprecian los efectos de borde, el campo eléctrico entre las placas de un condensador plano vacío va en la dirección normal a dichas placas, y viene dado por

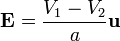
$\mathbf{E}=\frac{V_1-V_2}{a}\mathbf{u}$

siendo 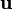$\mathbf{u}$ el vector unitario que apunta en la dirección de la placa 1 a la 2.

En nuestro caso, sea $\mathbf{u}_z$ el vector normal a todas las placas y en el sentido de la 1 a la 3. Los campos en cada región valen

Entre la placa exterior y la placa 1

$\mathbf{E}_{11}=-\frac{V_0}{a}\mathbf{u}_z$

Entre la 1 y la 2

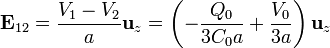
$\mathbf{E}_{12}=\frac{V_1-V_2}{a}\mathbf{u}_z= \left(-\frac{Q_0}{3C_0a}+\frac{V_0}{3a}\right)\mathbf{u}_z$

Entre la 2 y la 3

$\mathbf{E}_{23}=\frac{V_2-V_3}{a}\mathbf{u}_z= \left(-\frac{Q_0}{3C_0a}+\frac{V_0}{3a}\right)\mathbf{u}_z$

Entre la 3 y la placa exterior

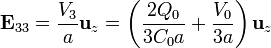
$\mathbf{E}_{33}=\frac{V_3}{a}\mathbf{u}_z= \left(\frac{2Q_0}{3C_0a}+\frac{V_0}{3a}\right)\mathbf{u}_z$

Dependiendo de los valores de $Q 0$ y $V 0$ , el campo puede ir en un sentido, en el otro, o incluso anularse en alguna de las regiones.

6 Conexión a tierra

Cuando se conecta la placa central a tierra, cambian las condiciones del problema. Esta placa deja de estar descargada, ya que ahora el cable de conexión permite que lleguen cargas a ella.

Si antes de la conexión $V 2$ era positivo (lo que ocurre si $Q 0 > 0$ y $V 0 > 0$ ), ahora entrará una carga negativa en la placa, que reducirá su potencial hasta hacerlo 0, siendo ahora $Q 2$ una cantidad negativa desconocida.

Además, al ser la placa central la que se pone a tierra, lo que hacemos es introducir un apantallamiento, que separa por completo el problema eléctrico a un lado de ella (que dependerá exclusivamente de $V 0$ ), del problema eléctrico al otro lado (que será sólo función de $Q 0$ ).

Matemáticamente debemos volver al sistema de ecuaciones anteriores, pero ahora con los datos

$V_1 = V_0\,$ $V_2=0\,$ $Q_3=Q_0\,$

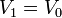
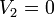
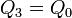
Sustituyendo de nuevo

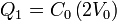
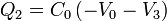
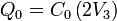
$Q_1 = C_0\left(2V_0\right)$ $Q_2=C_0\left(-V_0-V_3\right)$ $Q_0=C_0\left(2V_3\right)$

siendo la solución inmediata

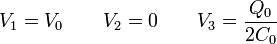
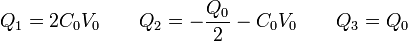
$V_1 = V_0\qquad V_2 = 0\qquad V_3 = \frac{Q_0}{2C_0}$ $Q_1 = 2C_0V_0\qquad Q_2 = -\frac{Q_0}{2}-C_0V_0 \qquad Q_3 = Q_0$

Y, para las placas exteriores

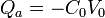
$Q_a = -C_0V_0\,$ $Q_b = -\frac{Q_0}{2}$

En términos de los condensadores equivalentes, este resultado es simple: la placa central a tierra separa el problea en dos. En cada lado tenemos dos condensadores en paralelo. Cada par forma un condensador equivalente de capacidad $2 C 0$ . Uno de ellos tiene una diferencia de potencial entre placas $V 0$ y el otro almacena una carga $Q 0$ en su placa positiva. A partir de aquí es inmediato obtener la carga de cada placa o su tensión.

La nueva energía almacenada será

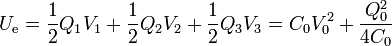
$U_\mathrm{e}=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2+\frac{1}{2}Q_3V_3 = C_0V_0^2+\frac{Q_0^2}{4C_0}$

Esta energía equivale a la de dos condensadores de capacidad $2 C 0$

$U_\mathrm{e}=\frac{1}{2}\left(2C_0\right)V_0^2+\frac{Q_0^2}{2(2C_0)}= C_0V_0^2+\frac{Q_0^2}{4C_0}$

Cinco planos conductores

De Laplace

Contenido

1 Enunciado

2 Coeficientes de capacidad

3 Cargas y tensiones

4 Energía electrostática

5 Campo eléctrico

6 Conexión a tierra

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES