Dos hemisferios y una lámina conductora

De Laplace

Contenido

1 Enunciado
2 Cargas y potenciales
- 2.1 Usando los coeficientes de capacidad
- 2.2 Usando solo el circuito equivalente
3 Campo eléctrico
4 Energía electrostática
5 Cambios en las conexiones

1 Enunciado

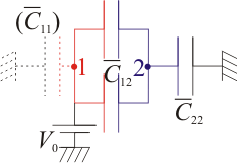
Se tiene un sistema formado por dos conductores hemisféricos de radio

R

. Estas dos semiesferas están separadas una pequeña distancia

2 a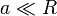

( $a\ll R$ ). En el espacio entre las dos semiesferas se encuentra una fina chapa circular de radio

R

y separada una distancia

a

de cada hemisferio.

Las dos semiesferas están conectadas por un hilo conductor en todo momento.

Suponga que la chapa se encuentra a una tensión $V 0$ mientras que el conjunto de las dos semiesferas está aislado y descargado. ¿Cuánto valen la cargas almacenadas y las tensiones de cada conductor?
Para el caso anterior de las expresiones aproximadas para el campo entre la chapa y los hemisferios, y en el exterior de estos.
Calcule la energía electrostática almacenada en este sistema.
Suponga que se desconecta la fuente $V 0$ y, acto seguido, se ponen los hemisferios a tierra. ¿Cuáles son las nuevas cargas, tensiones y energía almacenada?

Desprecie los efectos de borde.

2 Cargas y potenciales

2.1 Usando los coeficientes de capacidad

Este sistema está formado por solo dos conductores, ya que las semiesferas están conectadas en todo momento, de forman que se comportan de forma solidaria. llmamaremos “1” a la placa central y “2” a la asociación de los dos hemisferios.

La matriz de coeficientes de capacidad tendrá tres elementos independientes

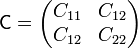
$\mathsf{C}=\begin{pmatrix}C_{11} & C_{12}\\ C_{12} & C_{22}\end{pmatrix}$

Estos coeficientes pueden calcularse a partir del circuito equivalente, el cual estará formado, en principio por tres condensadores.

El condensador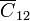 $\overline{C}_{12}$ es el que forma la placa central con las dos semiesferas. Su capacidad corresponde a la asociación en paralelo de dos condensadores planos, de sección

π R 2

y distancia entre placas

a

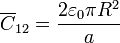
. Por ello, $\overline{C}_{12}= \frac{2\varepsilon_0 \pi R^2}{a}$

El condensador 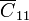$\overline{C}_{11}$ corresponde a las líneas de campo que van de la placa central a tierra (el infinito). Sin embargo, si despreciamos los efectos de borde, todas las líneas de campo del conductor 1 van a parar al 2, esto es, el 1 se encuentra en influencia total con el 2. Al no haber líneas que vayan del 1 al infinito

$\overline{C}_{11} = 0$

El condensador 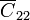$\overline{C}_{22}$ describe el exterior del conjunto de dos hemisferios. Al despreciar los fectos de borde, este sistema puede aproximarse por una sola esfera conductora, por lo que su autocapacidad vale

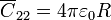
$\overline{C}_{22}=4\pi\varepsilon_0R$

La relación entre las cargas y los potenciales, a partir del circuito equivalente, será

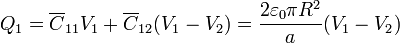
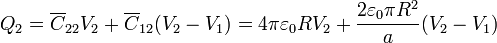
$Q_1 = \overline{C}_{11}V_1 + \overline{C}_{12}(V_1-V_2) = \frac{2\varepsilon_0\pi R^2}{a}(V_1-V_2)$ $Q_2 = \overline{C}_{22}V_2 + \overline{C}_{12}(V_2-V_1) = 4\pi\varepsilon_0RV_2+\frac{2\varepsilon_0\pi R^2}{a}(V_2-V_1)$

o, en forma matricial

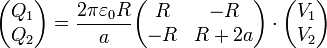
$\begin{pmatrix}Q_1\\ Q_2 \end{pmatrix}=\frac{2\pi\varepsilon_0R}{a}\begin{pmatrix}R & -R \\ -R & R+2a\end{pmatrix}\cdot\begin{pmatrix}V_1\\ V_2 \end{pmatrix}$

En el primer apartado, los datos son que la tensión de conductor 1 es $V 0$ y la carga del segundo es nula. Sustituyendo en las relaciones anteriores obtenemos el potencial de los dos hemisferios, que no es nulo, aunque estén descargados,

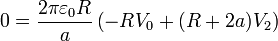
$0 = \frac{2\pi\varepsilon_0R}{a}\left(-RV_0+(R+2a)V_2\right)$ $\Rightarrow$ $V_2 = \frac{R}{R+2a}V_0$

y de aquí hallamos la carga en la chapa central

$Q_1 = \frac{2\pi\varepsilon_0R^2}{a}\left(V_0-V_2\right) = \frac{4\pi\varepsilon_0R^2}{R+2a}V_0$

2.2 Usando solo el circuito equivalente

Estos resultados pueden calcularse empleando exclusivamente el circuito equivalente, sin pasar por la forma matricial. Para ello observamos que, al estar el nodo 2 descargado, el condensador 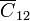$\overline{C}_{12}$ se encuentra en serie con el 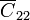$\overline{C}_{22}$ , cumpliendo la capacidad equivalente de la asociación

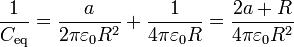
$\frac{1}{C_\mathrm{eq}}= \frac{a}{2\pi\varepsilon_0R^2}+\frac{1}{4\pi\varepsilon_0 R}= \frac{2a+R}{4\pi\varepsilon_0R^2}$ $\Rightarrow$ $C_\mathrm{eq}=\frac{4\pi\varepsilon_0R^2}{R+2a}$

la carga del conductor 1 corresponde a la almacenada en la placas positiva del condensador equivalente

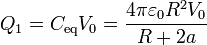
$Q_1 = C_\mathrm{eq}V_0 = \frac{4\pi\varepsilon_0R^2V_0}{R+2a}$

La tensión del nodo 2 la sacamos de que conocemos la carga del condensador 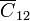$\overline{C}_{12}$ (la que acabamos de calcular) y su capacidad

$V_2 = \frac{Q_1}{\overline{C}_{12}}= \frac{C_\mathrm{eq}}{\overline{C}_{12}}V_0 = \frac{R}{R+2a}V_0$

3 Campo eléctrico

Para hallar el campo eléctrico no nos basta el circuito equivalente o la forma matricial, sino que debemos conocer el potencial no solo en los conductores, sino en todo el espacio.

No obstante, tanto en el caso de un condensador plano como en el de un conductor esférico las expresiones para el campo son sencillas.

Entre la chapa y los hemisferios, el campo tendrá por mósulo

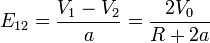
$E_{12}= \frac{V_1-V_2}{a} = \frac{2V_0}{R+2a}$

e irá en la dirección y sentido que va de la placa hacia cada hemisferio (hacia arriba en la parte superior y hacia abajo en la parte inferior).

En el exterior de los hemisferios el campo se puede aproximar por el de un conductor esférico

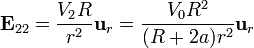
$\mathbf{E}_{22} = \frac{V_2R}{r^2}\mathbf{u}_r = \frac{V_0R^2}{(R+2a)r^2}\mathbf{u}_r$

4 Energía electrostática

La energía electrostática de un sistema de conductores es

$U_\mathrm{e}=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2 = \frac{1}{2}\,\frac{4\pi\varepsilon_0 R^2}{R+2a}\,V_0^2+\frac{1}{2}0\cdot V_2 = \frac{2\pi\varepsilon_0 R^2 V_0^2}{R+2a}$

o, en términos del cicuito equivalente

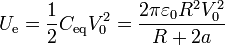
$U_\mathrm{e}=\frac{1}{2}C_\mathrm{eq}V_0^2=\frac{2\pi\varepsilon_0 R^2 V_0^2}{R+2a}$

5 Cambios en las conexiones

Al desconectar la fuente del conductor 1 la carga de éste queda fijada, ya que no puede llegar nueva carga o salir del conductor. A partir de ese momento

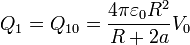
$Q_1 = Q_{10}=\frac{4\pi\varepsilon_0 R^2}{R+2a}V_0$

Si a continuación ponemos los hemisferios a tierra, estamos cortocircuitando el condensador 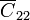$\overline{C}_{22}$ . En términos del campo eléctrico, al desaparecer la diferencia de potencial entre los hemisferios y el infinito, el campo exterior se anula.

Esto quiere decir que la nueva tensión del conductor 1 la da

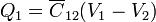
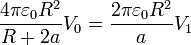
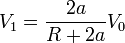
$Q_1 =\overline{C}_{12}(V_1-V_2)$ $\frac{4\pi\varepsilon_0 R^2}{R+2a}V_0=\frac{2\pi\varepsilon_0 R^2}{a}V_1$ $\Rightarrow$ $V_1 = \frac{2a}{R+2a}V_0$

mientras que la carga de las semiesferas es sencillamente

$Q_2 = \overline{C}_{12}(V_2-V-1) = -Q_1 = \frac{4\pi\varepsilon_0 R^2}{R+2a}V_0$

La nueva energía almacenada es

$U_\mathrm{e}=\frac{1}{2}Q_1V_1 + \frac{1}{2}Q_2V_2 = \frac{1}{2}\left(\frac{4\pi\varepsilon_0 R^2}{R+2a}V_0\right)\left(\frac{2a}{R+2a}V_0\right)+\frac{1}{2}Q_2\cdot 0 = \frac{4\pi\varepsilon_0 R^2a}{(R+2a)^2}V_0^2$

Esta energía es inferior a la anterior ya que

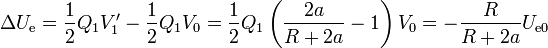
$\Delta U_\mathrm{e} = \frac{1}{2}Q_1V'_1-\frac{1}{2}Q_1V_0 = \frac{1}{2}Q_1\left(\frac{2a}{R+2a}-1\right)V_0 = -\frac{R}{R+2a}U_\mathrm{e0}$

En términos del circuito equivalente disminuye porque el 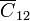$\overline{C}_{12}$ sigue cargado con la misma carga, pero el 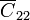$\overline{C}_{22}$ ha sido cortocircuitado, disipándose la energía de este segundo condensador.

El proceso de disipación se produce por medio de las corrientes que aparecen en el periodo transitorio que sigue a la conexión.

Dos hemisferios y una lámina conductora

De Laplace

Contenido

1 Enunciado

2 Cargas y potenciales

2.1 Usando los coeficientes de capacidad

2.2 Usando solo el circuito equivalente

3 Campo eléctrico

4 Energía electrostática

5 Cambios en las conexiones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES