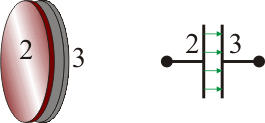Entrar Página Discusión Historial Go to the site toolbox

Dos planos y tres superficies esféricas

De Laplace

Contenido

1 Enunciado

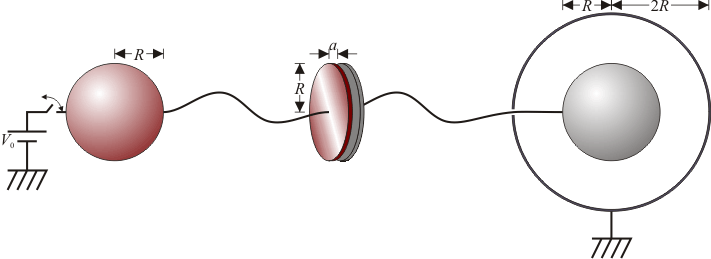
Dos discos conductores de radio 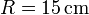R = 15\,\mathrm{cm}, paralelos y separados una distancia 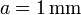a=1\,\mathrm{mm} están conectados a sendas esferas conductoras, también de radio R, mediante unos hilos conductores muy largos. Una de las esferas está completamente rodeada por una carcasa conductora esférica, conectada a tierra, de radio 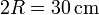2R = 30\,\mathrm{cm}, espesor despreciable, y concéntrica con la esfera. El sistema de conductores se encuentra en el vacío.

  1. Determine la matriz de coeficientes de capacidad del sistema en función de sus parámetros geométricos. Justifique las aproximaciones que haga.
  2. Estando el sistema inicialmente descargado, se conecta la esfera sin carcasa a una fuente de potencial fijo 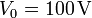V_0 = 100\,\mathrm{V}. Determine la carga eléctrica en cada una de las superficies conductoras (esferas, discos y carcasa esférica) cuando el sistema ha alcanzado el equilibrio electrostático.
  3. Para la situación anterior, determine la energía almacenada en el sistema.
Imagen:2planos3esferas.gif

2 Introducción

Este problema puede abordarse de múltiples formas equivalentes

  • Empleando exclusivamente el circuito equivalente.
  • Empleando exclusivamente coeficientes de capacidad, con ayuda del cálculo matricial.
  • Empleando una combinación de ambas técnicas.

Lo más habitual es el tercer método. Sin embargo, dado que los posibles saltos de un método a otro son numerosos y con el objeto de simplificar la exposición, aquí se va a explicar, en primer lugar, una solución que emplea casi únicamente el circuito; a continuación, una solución centrada en el álgebra matricial; finalmente, se comentarán diversas posibilidades intermedias.

Quede claro que ninguno de estos métodos es “el correcto” o “el preferible”. Todos son equivalentes, con tal de que proporcionen el resultado correcto.

3 Solución mediante el circuito equivalente

3.1 Construcción del circuito

Para construir el circuito equivalente debemos colocar en primer lugar un nodo por cada conductor. Este sistema consta, en principio, de 5 conductores:

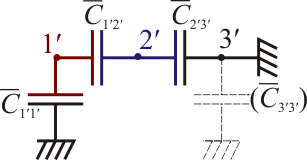
  1. La esfera de radio R, a la izquierda en la figura.
  2. La placa de la izquierda del condensador plano.
  3. La placa de la derecha del condensador plano.
  4. La esfera interior a la derecha en la figura.
  5. La carcasa esférica que rodea a la esfera anterior.

Sin embargo, al existir una conexión entre el 1 y el 2, y otra entre el 3 y el 4, el sistema consta realmente de tres conductores, que denominaremos, respectivamente 1' (la unión de 1 y 2), 2' (unión de 3 y 4) y 3' (la carcasa). En lo que sigue, es importante no confundir los conductores considerados como un sistema de 5 (lo que se indica con números sin prima) y considerados como un sistema de 3 (lo que se indica con números con prima).


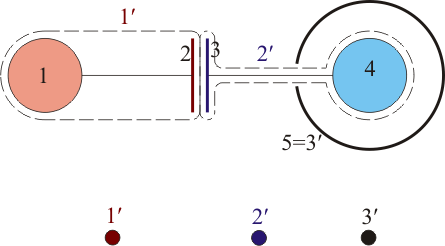
Imagen:2planos3esferas01.gif

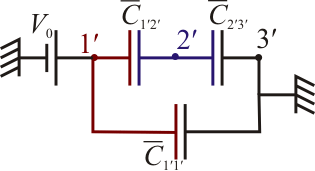
Colocamos entonces un nodo por cada uno de estos tres conductores.

A continuación debemos colocar un condensador entre cada par de nodos, representando la capacidad que existe entre ellos.

Entre los nodos 1' y 2' se encuentra un condensador plano. Teniendo en cuenta que la separación entre placas (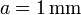a=1\,\mathrm{mm}) es mucho menor que su radio (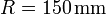R=150\,\mathrm{mm}), podemos despreciar los efectos de borde y aproximar la capacidad por

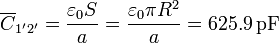
\overline{C}_{1'2'}=\frac{\varepsilon_0 S}{a}=\frac{\varepsilon_0 \pi R^2}{a} = 625.9\,\mathrm{pF}

En este cálculo estamos despreciando además las posibles líneas de campo entre la esfera 1 y el conductor 2'. Ya que los hilos son muy largos, podemos suponer que cada uno de sus tres partes se comporta de forma independiente salvo por el hecho de que los hilos igualan los potenciales.

Por la misma razón, no hay condensador entre el nodo 1' y el 3', ya que ninguna línea de campo de la esfera de la izquierda llega a la carcasa de la derecha.

\overline{C}_{1'3'} = 0

Por último, entre el conductor 2' y el 3' tenemos la capacidad de un condensador esférico de radios R y 2R

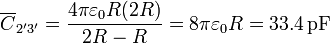
\overline{C}_{2'3'} = \frac{4\pi\varepsilon_0 R(2R)}{2R-R} = 8\pi\varepsilon_0 R = 33.4\,\mathrm{pF}

Además de estas capacidades, debemos añadir las autocapacidades que conectan cada conductor a tierra.

Para el conductor 1', las líneas que van al infinito son las que parten de la esfera 1, la cual tiene una capacidad

\overline{C}_{1'1'}=4\pi\varepsilon_0 R = 16.7\,\mathrm{pF}

Ninguna de las dos partes del conductor 2' produce líneas que vayan al infinito. Las de la placa plana van a la otra placa y las de la esfera van a la carcasa. Por tanto

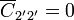
\overline{C}_{2'2'} = 0

Por último, el el conductor 3', visto desde el exterior se comporta como una esfera de radio 2R, de autocapacidad

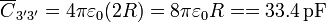
\overline{C}_{3'3'}=4\pi\varepsilon_0(2R) = 8\pi\varepsilon_0 R = = 33.4\,\mathrm{pF}
Esto nos deja finalmente con un circuito equivalente formado por tres nodos y cuatro condensadores.

Conocidas las capacidades y autocapacidades obtenemos los coeficientes de capacidad e inducción

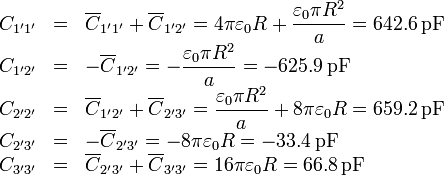
\begin{array}{rcl} C_{1'1'}&=&\overline{C}_{1'1'} +\overline{C}_{1'2'}=4\pi\varepsilon_0 R + \displaystyle\frac{\varepsilon_0 \pi R^2}{a} = 642.6\,\mathrm{pF}\\ C_{1'2'}& = &-\overline{C}_{1'2'} = \displaystyle-\frac{\varepsilon_0\pi R^2}{a} = -625.9\,\mathrm{pF}\\ C_{2'2'}& = &\overline{C}_{1'2'}+\overline{C}_{2'3'} = \displaystyle\frac{\varepsilon_0 \pi R^2}{a} + 8\pi\varepsilon_0 R = 659.2\,\mathrm{pF}\\ C_{2'3'}& = &-\overline{C}_{2'3'} = -8\pi\varepsilon_0 R = -33.4\,\mathrm{pF}\\ C_{3'3'}& = & \overline{C}_{2'3'}+\overline{C}_{3'3'} = 16\pi\varepsilon_0 R = 66.8\,\mathrm{pF}\\ \end{array}

o, en forma matricial

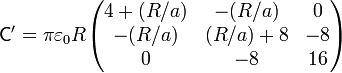
\mathsf{C}'= \pi\varepsilon_0 R\begin{pmatrix} 4 + (R/a) & -(R/a) & 0 \\ -(R/a) & (R/a) + 8 & -8 \\ 0 & -8 & 16\end{pmatrix}

Numéricamente

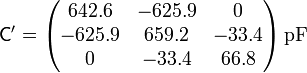
\mathsf{C}'= \begin{pmatrix}642.6 & -625.9 & 0 \\ -625.9 & 659.2 & -33.4 \\ 0 & -33.4 & 66.8\end{pmatrix}\,\mathrm{pF}

Vemos que, como debe ser, los elementos de la diagonal son estrictamente positivos, mientras que los no diagonales son negativos o nulos.

Este sistema puede incluso suponerse como formado por solo dos conductores, aplicando el que el conductor 3' se encuentra permanentemente a tierra. Desde el punto de vista del circuito equivalente, lo que ocurre es que al conectar el nodo 3' a tierra, se cortocircuita el condensador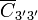 \overline{C}_{3'3'}. El sistema se reduce a los nodos 1' y 2'. A todos los efectos, el conductor 3' es equivalente al infinito, ya que se encuentran al mismo potencial.

Esto deja las relaciones para las cargas y los potenciales como

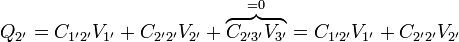
Q_{1'}=C_{1'1'}V_{1'}+C_{1'2'}V_{2'} + \overbrace{C_{1'3'}V_{3'}}^{=0} =C_{1'1'}V_{1'}+C_{1'2'}V_{2'}         Q_{2'}=C_{1'2'}V_{1'}+C_{2'2'}V_{2'} + \overbrace{C_{2'3'}V_{3'}}^{=0}=C_{1'2'}V_{1'}+C_{2'2'}V_{2'}

esto es, que el sistema se puede representar por una matriz 2×2.

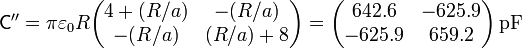
\mathsf{C}''= \pi\varepsilon_0 R\begin{pmatrix} 4 + (R/a) & -(R/a) \\ -(R/a) & (R/a) + 8\end{pmatrix}=\begin{pmatrix}642.6 & -625.9\\ -625.9 & 659.2\end{pmatrix}\,\mathrm{pF}

Una vez que tenemos la matriz de coeficientes de capacidad, o el circuito equivalente, podemos calcular las cargas y potenciales en cada caso concreto.

3.2 Cargas y voltajes

Inicialmente tenemos el sistema descargado. Entonces se conecta el conductor 1' a tensión 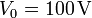V_0=100\,\mathrm{V}. El conductor 2' no se conecta a nada, por lo que sigue descargado.

Se trata de hallar V2', así como las cargas en las distintas superficies conductoras.

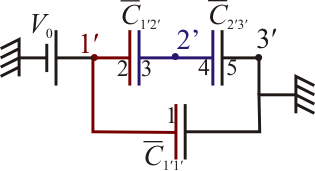
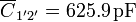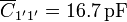Desde el punto de vista del circuito ello significa que añadimos una fuente de tensión al nodo 1', mientras que no conectamos nada al 2'. El nodo 3' sigue puesto a tierra. Tenemos que el condensador \overline{C}_{1'2'}= 625.9\,\mathrm{pF}$ se encuentra en serie con el \overline{C}_{2'3'}=33.4\,\mathrm{pF} y esta asociación se encuentra en paralelo con el \overline{C}_{1'1'}=16.7\,\mathrm{pF}.

La capacidad equivalente del circuito es por tanto

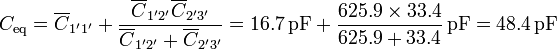
C_\mathrm{eq}=\overline{C}_{1'1'}+\frac{\overline{C}_{1'2'}\overline{C}_{2'3'}}{\overline{C}_{1'2'}+\overline{C}_{2'3'}}= 16.7\,\mathrm{pF} +\frac{625.9\times 33.4}{625.9+33.4}\,\mathrm{pF}= 48.4\,\mathrm{pF}

Conocida esta capacidad tenemos la carga del conductor 1':

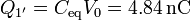
Q_{1'}=C_\mathrm{eq}V_0 = 4.84\,\mathrm{nC}

El potencial del nodo 2' lo obtenemos aplicando que la tensión V0 se reparte entre los dos condensadores en serie, por lo que

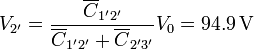
V_{2'}=\frac{\overline{C}_{1'2'}}{\overline{C}_{1'2'}+\overline{C}_{2'3'}}V_0 = 94.9\,\mathrm{V}

El problema nos pide no solo la carga neta de cada conductor, sino de cada superficie. Este cálculo es sencillo mediante el uso del circuito equivalente, ya que tenemos las distintas capacidades y potenciales.

La carga en la esfera es la del condensador 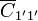\overline{C}_{1'1'}

Q_1 = \overline{C}_{1'1'}V_0 = 4\pi\varepsilon_0 R V_0 = 1.67\,\mathrm{nC}

La carga de las placas del condensador plano es igual a la capacidad por su diferencia de potencial

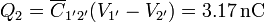
Q_2 = \overline{C}_{1'2'}(V_{1'} -V_{2'}) = 3.17\,\mathrm{nC}         Q_3 = -Q_2 =-3.17\,\mathrm{nC}

La carga de la esfera interior a la carcasa corresponde a la de una de las placas del condensador \overline{C}_{2'3'} y la de la carcasa a la de la otra placa. Como este condensador está en serie con el anterior, las cargas son las mismas que en aquel,

Q_4 = Q_2 = 3.17\,\mathrm{nC}        Q_5 = Q_3 = -3.17\,\mathrm{nC}

3.3 Energía almacenada

Una vez que tenemos las cargas y los potenciales, el cálculo de la energía es inmediato

U_\mathrm{e} = \frac{1}{2}\sum_{i=1}^3 Q_{i'}V_{i'} = \frac{1}{2}\left(4.84{\cdot}100+0{\cdot}V_{2'}+Q_{3'}{\cdot}0\right)=241.9\,\mathrm{nJ}

Obsérvese que al ser nulas la carga del segundo conductor y el potencial del tercero, nos quedamos con un solo sumando.

Empleando el circuito equivalente, esta energía se puede hallar sumando la almacenada en los distintos condensadores

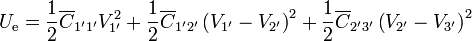
U_\mathrm{e}=\frac{1}{2}\overline{C}_{1'1'}V_{1'}^2 + \frac{1}{2}\overline{C}_{1'2'}\left(V_{1'}-V_{2'}\right)^2 + \frac{1}{2}\overline{C}_{2'3'}\left(V_{2'}-V_{3'}\right)^2

o directamente empleando la capacidad equivalente

U_\mathrm{e}=\frac{1}{2}C_\mathrm{eq} V_0^2

El resultado será el mismo en todos los casos.

4 Solución mediante la matriz de coeficientes de capacidad

4.1 Cálculo de la matriz

Un método complementario al uso del circuito equivalente consiste en analizar directamente el sistema en términos de los conductores que lo forman.

Este sistema consta, en principio, de 5 conductores:

  1. La esfera de radio R, a la izquierda en la figura.
  2. La placa de la izquierda del condensador plano.
  3. La placa de la derecha del condensador plano.
  4. La esfera interior a la derecha en la figura.
  5. La carcasa esférica que rodea a la esfera anterior.

Si consideramos el sistema como formado por cinco conductores, se trata de hallar una matriz 5×5.

Más tarde veremos como reducirlo a solo 3, teniendo en cuenta los hilos de conexión.

Dado que estos hilos son muy largos, podemos suponer el sistema de cinco conductores en realidad se compone de tres partes independientes:

  1. La esfera 1
  2. El condensador plano (conductores 2 y 3)
  3. La esfera con la carcasa (conductores 4 y 5)

El campo de cada una de las partes no llega a ninguna de las otras dos, por lo que el cálculo de los coeficientes de capacidad puede hacerse por separado. La presencia de los cables lo que hará será igualar los potenciales y redistribuir las cargas, pero no hace que que el campo de una parte llegue a alguna de las otras.

Matemáticamente, esto se expresa como que se anulan los coeficientes de capacidad que relacionan conductores de dos partes distintas, esto es

C_{12}=C_{13}=C_{14}=C_{15} = 0\,         C24 = C25 = C34 = C35 = 0

más sus expresiones simétricas.

En forma matricial, esto equivale a que la matriz de coeficientes de capacidad es de la forma

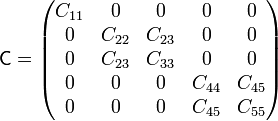
\mathsf{C}=\begin{pmatrix}C_{11} & 0 & 0 & 0 & 0 \\ 0 & C_{22} & C_{23} & 0 & 0 \\ 0 & C_{23} & C_{33} & 0 & 0 \\ 0 & 0 & 0 & C_{44} & C_{45} \\ 0 & 0 & 0 & C_{45} & C_{55}\end{pmatrix}

o, dicho de otra forma, que esta matriz está formada por bloques, siendo cada bloque el correspondiente a cada parte del sistema.

Veamos cuanto vale cada uno de esos bloques.

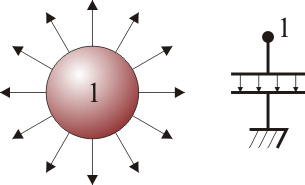
A. Para la esfera 1, se trata de un conductor esférico no sometido a la influencia de ningún otro conductor. Por tanto

C_{11} = 4\pi\varepsilon_0 R== 16.7\,\mathrm{pF}


B. los conductores 2 y 3 forman un condensador plano. Teniendo en cuenta que la separación entre placas ($a=1\,\mathrm{mm}$) es mucho menor que su radio $R=150\,\mathrm{mm}$, podemos despreciar los efectos de borde y aproximar la capacidad por

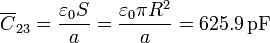
\overline{C}_{23}=\frac{\varepsilon_0 S}{a}=\frac{\varepsilon_0 \pi R^2}{a} = 625.9\,\mathrm{pF}

Dado que en un condensador plano prácticamente todo el campo se concentra entre las placas, podemos despreciar las autocapacidades

\overline{C}_{22} = \overline{C}_{33} = 0

de forma que la carga en cada conductor es

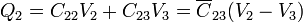
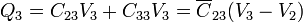
Q_2 = C_{22}V_2+C_{23}V_3 = \overline{C}_{23}(V_2-V_3)        Q_3 = C_{23}V_3 + C_{33}V_3= \overline{C}_{23}(V_3-V_2)

resultando los coeficientes de capacidad

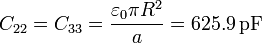
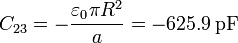
C_{22}=C_{33}=\frac{\varepsilon_0\pi R^2}{a}=625.9\,\mathrm{pF}        C_{23}=-\frac{\varepsilon_0\pi R^2}{a}=-625.9\,\mathrm{pF}

C. La tercera parte del sistema está formada por la esfera ``4 y la carcasa ``5. Cuando se encuentran a diferentes potenciales, en la esfera interior se almacena la carga correspondiente a un condensador esférico de capacidad

\overline{C}_{45} = \frac{4\pi\varepsilon_0 R(2R)}{(2R)-R} = 8\pi\varepsilon_0 R

por lo que

Q_4 = 8\pi\varepsilon_0 R(V_4-V_5)

En la carcasa esférica debemos contar la carga de este mismo condensador, que se almacena en su cara interior, más la de su superficie exterior, que equivale a la de un conductor esférico de capacidad

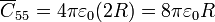
\overline{C}_{55} = 4\pi\varepsilon_0 (2R) = 8\pi\varepsilon_0 R

de forma que

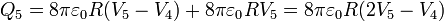
Q_5 = 8\pi\varepsilon_0 R(V_5-V_4) + 8\pi\varepsilon_0 R V_5 = 8\pi\varepsilon_0 R(2V_5-V_4)

Los coeficientes de capacidad para estos dos conductores valen, por tanto

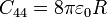
C_{44} = 8\pi\varepsilon_0 R\,        C_{45} = -8\pi\varepsilon_0 R\,         C_{55} = 16\pi\varepsilon_0 R

con valores numéricos

C_{44} = 33.4\,\mathrm{pF}\qquad C_{45}=-33.4\mathrm{pF}\qquad C_{55} = 66.8\,\mathrm{pF}

Con todo lo anterior, la matriz de coeficientes de capacidad para el sistema de cinco conductores queda, sacando factor común

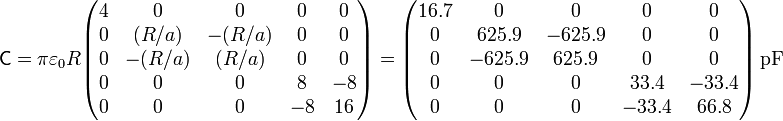
\mathsf{C}=\pi \varepsilon_0 R\begin{pmatrix}4 & 0 & 0 & 0 & 0 \\0 & (R/a) & -(R/a) & 0 & 0 \\ 0 & -(R/a) & (R/a) & 0 & 0 \\0 & 0 & 0 & 8 & -8 \\ 0 & 0 & 0 & -8 & 16\end{pmatrix} = \begin{pmatrix}16.7 & 0 & 0 & 0 & 0 \\ 0 & 625.9 & -625.9 & 0 & 0 \\ 0 & -625.9 & 625.9 & 0 & 0 \\ 0 & 0 & 0 & 33.4 & -33.4 \\ 0 & 0 & 0 & -33.4 & 66.8\end{pmatrix}\,\mathrm{pF}

Vemos que los términos diagonales son todos positivos y los no diagonales son negativos o nulos.

Ahora bien, en este problema los conductores se encuentran conectados por hilos conductores, que une el 1 con el 2, y el 3 con el 4. Esto reduce el sistema a uno de solo tres conductores: el 1' = 1 + 2, 2' = 3 + 4 y 3' = 5. Para este sistema reducido, la matriz de coeficientes de capacidad e inducción es una 3×3.

Podemos obtener esta matriz a partir de la matriz 5×5 que acabamos de calcular. Para ello definimos una matriz 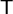\mathsf{T} que representa las conexiones efectuadas. En este caso, se trata de unir 1 con 2 y 3 con 4, lo que da la matriz

\mathsf{T} = \begin{pmatrix}1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\end{pmatrix}

La nueva matriz de coeficientes de capacidad es

\mathsf{C}'=\mathsf{T}{\cdot}\mathsf{C}{\cdot}\mathsf{T}^t =\pi\varepsilon_0 R \begin{pmatrix}1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\end{pmatrix}{\cdot}\begin{pmatrix}4 & 0 & 0 & 0 & 0 \\ 0 & (R/a) & -(R/a) & 0 & 0 \\ 0 & -(R/a) & (R/a) & 0 & 0 \\ 0 & 0 & 0 & 8 & -8 \\ 0 & 0 & 0 & -8 & 16\end{pmatrix}{\cdot} \begin{pmatrix}1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} =\pi\varepsilon_0 R\begin{pmatrix} 4 + (R/a) & -(R/a) & 0 \\-(R/a) & (R/a) + 8 & -8 \\ 0 & -8 & 16\end{pmatrix}

Numéricamente

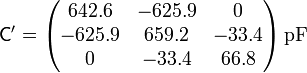
\mathsf{C}'= \begin{pmatrix} 642.6 & -625.9 & 0 \\ -625.9 & 659.2 & -33.4 \\0 & -33.4 & 66.8\end{pmatrix}\,\mathrm{pF}

Este sistema puede incluso suponerse como formado por solo dos conductores, aplicando el que el conductor 3' (o el 5, que es el mismo) se encuentra permanentemente a tierra. Esto deja las relaciones para las cargas y los potenciales como

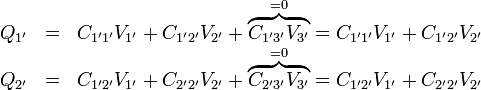
\begin{array}{rcl}Q_{1'}&=&C_{1'1'}V_{1'}+C_{1'2'}V_{2'} + \overbrace{C_{1'3'}V_{3'}}^{=0} =C_{1'1'}V_{1'}+C_{1'2'}V_{2'}\\ Q_{2'}&=&C_{1'2'}V_{1'}+C_{2'2'}V_{2'} + \overbrace{C_{2'3'}V_{3'}}^{=0} =C_{1'2'}V_{1'}+C_{2'2'}V_{2'}\end{array}

esto es, que el sistema se puede representar por una matriz 2×2.

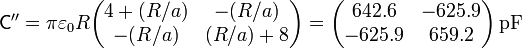
\mathsf{C}''= \pi\varepsilon_0 R\begin{pmatrix} 4 + (R/a) & -(R/a) \\ -(R/a) & (R/a) + 8\end{pmatrix}= \begin{pmatrix}642.6 & -625.9\\-625.9 & 659.2\end{pmatrix}\,\mathrm{pF}

4.2 Cargas y potenciales

En este apartado, tenemos un caso particular de cargas y potenciales. Los datos que conocemos son, por un lado,

Q_{2'}=0\,

ya que este conductor está aislado y se encontraba inicialmente descargado; por otro

V_{1'} = V_0\,

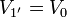
al conectarse a la fuente. El conductor 3' sigue verificando

V_{3'}=0\,

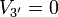
El calculo de las restantes cargas y potenciales es inmediato a partir de los coeficientes de capacidad. Tenemos el sistema de ecuaciones

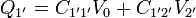
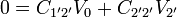
Q_{1'}=C_{1'1'}V_0 + C_{1'2'}V_{2'}\,        0 = C_{1'2'}V_0 + C_{2'2'}V_{2'}\,

de donde

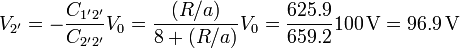
V_{2'}= - \frac{C_{1'2'}}{C_{2'2'}}V_0 = \frac{(R/a)}{8+(R/a)}V_0 = \frac{625.9}{659.2}100\,\mathrm{V}=96.9\,\mathrm{V}

La carga total del primer conductor es

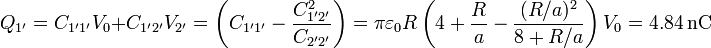
Q_{1'} = C_{1'1'}V_0 + C_{1'2'}V_{2'}=\left(C_{1'1'}-\frac{C_{1'2'}^2}{C_{2'2'}}\right) =\pi\varepsilon_0 R\left(4+\frac{R}{a}-\frac{(R/a)^2}{8+R/a}\right)V_0 = 4.84\,\mathrm{nC}

El problema nos pide no solo la carga neta de cada conductor, sino de cada superficie. Podemos aplicar que conocemos la matriz de coeficientes de capacidad del sistema de cinco conductores, y hemos calculado los potenciales de los cinco conductores

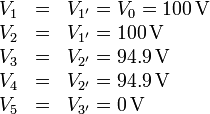
\begin{array}{rcl}V_1 &= &V_{1'}= V_0 = 100\,\mathrm{V}\\V_2 &= &V_{1'} = 100\,\mathrm{V}\\ V_3 & = & V_{2'} = 94.9\,\mathrm{V}\\ V_4 & = & V_{2'}= 94.9\,\mathrm{V}\\ V_5 & = & V_{3'}=0\,\mathrm{V}\end{array}

lo que nos da

\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3 \\ Q_4 \\ Q_5\end{pmatrix}=\begin{pmatrix}16.7 & 0 & 0 & 0 & 0 \\ 0 & 625.9 & -625.9 & 0 & 0 \\ 0 & -625.9 & 625.9 & 0 & 0 \\ 0 & 0 & 0 & 33.4 & -33.4 \\ 0 & 0 & 0 & -33.4 & 66.8\end{pmatrix}\cdot\begin{pmatrix}100 \\ 100 \\ 94.9 \\ 94.9 \\ 0\end{pmatrix}\,\mathrm{pC}= \begin{pmatrix}1.67 \\ 3.17 \\ -3.17 \\ 3.17 \\ -3.17\end{pmatrix} \,\mathrm{nC}

La ventaja de este método es que permite hallar de una vez todas las cargas. El inconveniente, que requiere el uso del álgebra matricial.

4.3 Energía almacenada

Una vez que tenemos las cargas y los potenciales, el cálculo de la energía es inmediato

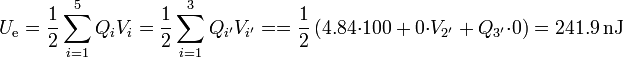
U_\mathrm{e} = \frac{1}{2}\sum_{i=1}^5 Q_i V_i = \frac{1}{2}\sum_{i=1}^3 Q_{i'}V_{i'} = =\frac{1}{2}\left(4.84{\cdot}100+0{\cdot}V_{2'}+Q_{3'}{\cdot}0\right)=241.9\,\mathrm{nJ}

Obsérvese que al ser nulas la carga del segundo conductor y el potencial del tercero, nos quedamos con un solo sumando.

Si se desea emplear el álgebra matricial, la energía se calcula como

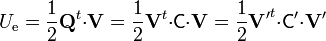
U_\mathrm{e} = \frac{1}{2}\mathbf{Q}^t{\cdot}\mathbf{V} = \frac{1}{2}\mathbf{V}^t{\cdot}\mathsf{C}{\cdot}\mathbf{V} = \frac{1}{2}\mathbf{V'}^t{\cdot}\mathsf{C'}{\cdot}\mathbf{V'}

El resultado en cualquier caso es exactamente el mismo.

5 Posibles caminos intermedios

Evidentemente, no hay obligación de restringirse al circuito equivalente o usar exclusivamente álgebra matricial para resolver el problema. En cualquier momento puede pasarse de un planteamiento al otro, siempre que ello conduzca al resultado correcto. Es importante, eso sí, tener claros los distintos conceptos y no confundir los coeficientes de capacidad, Cik, con las capacidades y autocapacidades 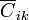\overline{C}_{ik}.

Entre los posibles ataques mixtos, pueden encontrarse los siguientes:

1) Usar el circuito equivalente para obtener la matriz 5×5. En este caso, se considera el sistema como formado por tres partes independientes, cada una con su circuito:

  1. La esfera 1, equivalente a un condensador esférico de radio interior R y radio exterior infinito.
  2. El condensador de placas planas 2 y 3.
  3. La esfera 4 y la carcasa 5, que se modelan como dos condensadores, uno esférico entre ambos conductores y otro esférico entre la carcasa y el infinito.

Una vez que se han calculado estas capacidades y autocapacidades, y sabiendo que el resto de las capacidades son nulas, pueden hallarse los coeficientes de capacidad a través de las fórmulas

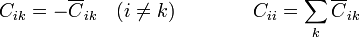
C_{ik} = -\overline{C}_{ik}\quad (i\neq k)\qquad\qquad C_{ii}=\sum_k \overline{C}_{ik}

Luego, para pasar a un sistema de tres conductores puede emplearse el álgebra matricial.

2) Otra posibilidad sencilla consiste en emplear el circuito equivalente para todo el primer apartado, pero recurrir a las matrices para los apartados segundo y tercero.

3) Los cálculos para hallar cargas o potenciales pueden hacerse también empleando sistemas de ecuaciones en lugar de matrices. Por ejemplo, si no se conoce el uso de la matriz 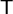\mathsf{T} se puede reducir el sistema de cinco conductores a uno de tres observando que, como resultado de la conexión entre 1 y 2, y entre 3 y 4, tenemos las relaciones

V_1 = V_2 = V_{1'}\qquad Q_{1'}=Q_1+Q_2        V_3 = V_4 = V_{2'}\qquad Q_{2'}=Q_3+Q_4 que conduce a los mismos resultados.
Obtenido de "http://tesla.us.es/wiki/index.php/Dos_planos_y_tres_superficies_esf%C3%A9ricas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:56, 20 ene 2010. - Esta página ha sido visitada 7.403 veces. - Aviso legal - Acerca de Laplace