Dos placas conductoras y una densidad de carga intermedia

De Laplace

Contenido

1 Enunciado
2 Potencial y campo eléctrico
- 2.1 Potencial
- 2.2 Campo
3 Energía electrostática
- 3.1 A partir de las cargas
- 3.2 A partir de los campos
4 Fuerzas

1 Enunciado

Dos placas metálicas, planas y paralelas, de sección $S$ , se encuentran situadas a una distancia $a$ la una de la otra. La placa inferior se pone a una tensión $V 0$ , mientras que la superior se encuentra a tierra. El espacio entre las placas está ocupado por una capa de un material cargado con una densidad uniforme $ρ 0$ .

Determine el potencial y el campo eléctrico en todos los puntos entre las placas.
Calcule la energía eléctrica almacenada en el sistema.
Halle la fuerza sobre las placas y sobre el material intermedio.

2 Potencial y campo eléctrico

2.1 Potencial

En este problema debemos resolver la ecuación de Poisson

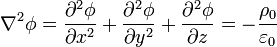
$\nabla^2 \phi = \frac{\partial^2\phi}{\partial x^2}+ \frac{\partial^2\phi}{\partial y^2}+ \frac{\partial^2\phi}{\partial z} = -\frac{\rho_0}{\varepsilon_0}$

con condiciones de contorno de Dirichlet

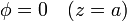
$\phi = V_0\quad (z=0)$ $\phi=0\quad(z=a)$

Dado que ni la densidad de carga ni las condiciones de contorno dependen de $x$ ni de $y$ , salvo en el hecho de que las placas tienen una extensión $S$ , podemos hacer la aproximación de despreciar los efectos de borde y suponer que el potencial depende exclusivamente de la coordenada $z$ . Esto reduce la ecuación de Poisson a

$\frac{\mathrm{d}^2\phi}{\mathrm{d}z^2}=-\frac{\rho_0}{\varepsilon_0}$

con solución

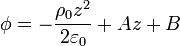
$\phi = -\frac{\rho_0 z^2}{2\varepsilon_0}+ A z + B$

Las constantes $A$ y $B$ las obtenemos de las condiciones de contorno

$V_0 = B\,$ $0 = -\frac{\rho_0 a^2}{2\varepsilon_0}+ Aa + B$

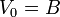
resultando finalmente las constantes y el potencial

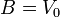
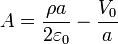
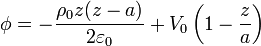
$B = V_0\,$ $A = \frac{\rho a}{2\varepsilon_0}-\frac{V_0}{a}$ $\phi = -\frac{\rho_0z(z-a)}{2\varepsilon_0} + V_0\left(1-\frac{z}{a}\right)$

Esta solución puede escribirse como la superposición

φ = φ 0 + V 0 φ 1

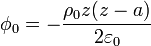
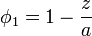
$\phi_0 = -\frac{\rho_0z(z-a)}{2\varepsilon_0}$ $\phi_1 = 1-\frac{z}{a}$

siendo 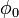$\phi_0\,$ el potencial que habría entre las placas si estuviera presente la carga pero los conductores estuvieran a tierra. 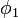$\phi_1\,$ representa el potencial que habría si la carga estuviera ausente, la placa inferior estuviera a potencial unidad y la superior a tierra.

2.2 Campo

Conocido el potencial determinamos el campo a partir de su gradiente

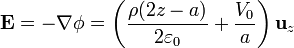
$\mathbf{E} = -\nabla\phi = \left(\frac{\rho (2z-a)}{2\varepsilon_0} +\frac{V_0}{a}\right)\mathbf{u}_{z}$

Este campo varía linealmente desde un valor

$\mathbf{E}_0= \left(-\frac{\rho a}{2\varepsilon_0} +\frac{V_0}{a}\right)\mathbf{u}_{z}$

en $z = 0$ hasta

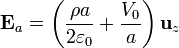
$\mathbf{E}_a= \left(\frac{\rho a}{2\varepsilon_0} +\frac{V_0}{a}\right)\mathbf{u}_{z}$

en $z = a$ .

3 Energía electrostática

La energía almacenada la podemos determinar a partir de las cargas o de los campos.

3.1 A partir de las cargas

Por el primer método tenemos la expresión

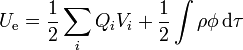
$U_\mathrm{e} = \frac{1}{2}\sum_i Q_i V_i + \frac{1}{2}\int\rho\phi\,\mathrm{d}\tau$

Debemos determinar la carga en cada conductor. Conociendo el campo en su superficie podemos hallar la densidad de carga superficial y a partir de esta la carga de cada uno.

<center> $\sigma_{s1}=\varepsilon_0\mathbf{n}{\cdot}[\mathbf{E}] = \varepsilon_0\mathbf{u}_{z}{\cdot}\left(\mathbf{E}_0-\mathbf{0}\right) = -\frac{\rho a}{2}+\frac{\varepsilon_0 V_0}{a}$ $\sigma_{s2}=\varepsilon_0\mathbf{n}{\cdot}[\mathbf{E}] = \varepsilon_0\mathbf{u}_{z}{\cdot}\left(\mathbf{0}-\mathbf{E}_a\right) = -\frac{\rho a}{2}-\frac{\varepsilon_0 V_0}{a}$ $Q_1= -\frac{\rho a S}{2}+\frac{\varepsilon_0 S V_0}{a}\qquad Q_2= -\frac{\rho a S}{2}-\frac{\varepsilon_0 S V_0}{a}$

resultando, para la energía

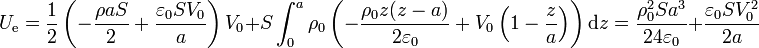
$U_\mathrm{e} = \frac{1}{2}\left(-\frac{\rho a S}{2}+\frac{\varepsilon_0 S V_0}{a}\right)V_0+ S\int_0^a \rho_0\left(-\frac{\rho_0z(z-a)}{2\varepsilon_0}+V_0\left(1-\frac{z}{a}\right)\right)\mathrm{d}z= \frac{\rho_0^2 S a^3}{24\varepsilon_0}+\frac{\varepsilon_0 S V_0^2}{2a}$

3.2 A partir de los campos

Alternativamente, podemos calcular la energía a partir de su densidad

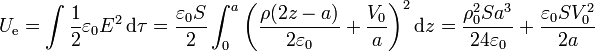
$U_\mathrm{e} = \int \frac{1}{2}\varepsilon_0 E^2\,\mathrm{d}\tau =\frac{\varepsilon_0 S}{2}\int_0^a\left(\frac{\rho (2z-a)}{2\varepsilon_0} +\frac{V_0}{a}\right)^2\mathrm{d}z =\frac{\rho_0^2 S a^3}{24\varepsilon_0}+\frac{\varepsilon_0 S V_0^2}{2a}$

Obsérvese que para hallar la integral de volumen, debemos extenderla, en principio, a todo el espacio, solo que en este sistema suponemos que sólo hay campo en el espacio entre las placas. Al ser la densidad de energía una cantidad estratificada (dependiente solo de $z$ ) la integral de volumen equivale al producto de la sección $S$ por la integral en $z$ .

4 Fuerzas

La fuerza sobre las placas la podemos calcular a partir de la presión en su superficie.

Sobre la placa inferior la fuerza por unidad de superficie es

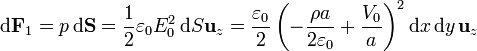
$\mathrm{d}\mathbf{F}_1 = p\,\mathrm{d}\mathbf{S} = \frac{1}{2}\varepsilon_0E_0^2\,\mathrm{d}S\mathbf{u}_{z} = \frac{\varepsilon_0}{2}\left(-\frac{\rho a}{2\varepsilon_0} +\frac{V_0}{a}\right)^2\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_{z}$

La fuerza la hallamos integrando sobre toda la sección

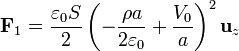
$\mathbf{F}_1 = \frac{\varepsilon_0 S}{2}\left(-\frac{\rho a}{2\varepsilon_0}+\frac{V_0}{a}\right)^2\mathbf{u}_{z}$

Un cálculo análogo nos da la fuerza sobre la placa superior (teniendo en cuenta que la normal debe ser 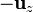$-\mathbf{u}_{z}$ )

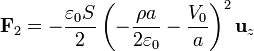
$\mathbf{F}_2 = -\frac{\varepsilon_0 S}{2}\left(-\frac{\rho a}{2\varepsilon_0}-\frac{V_0}{a}\right)^2\mathbf{u}_{z}$

La fuerza sobre la carga de volumen la hallamos aplicando la tercera ley de Newton

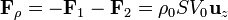
$\mathbf{F}_\rho = -\mathbf{F}_1 - \mathbf{F}_2 = \rho_0 S V_0\mathbf{u}_{z}$

vemos que, si la densidad de carga es positiva, la fuerza va en la dirección de mayor a menor potencial, y que no aparece ningún efecto de fuerza de la densidad de carga sobre sí misma.

Dos placas conductoras y una densidad de carga intermedia

De Laplace

Contenido

1 Enunciado

2 Potencial y campo eléctrico

2.1 Potencial

2.2 Campo

3 Energía electrostática

3.1 A partir de las cargas

3.2 A partir de los campos

4 Fuerzas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES