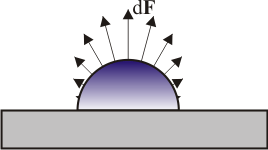
Fuerza sobre una partícula semiesférica

De Laplace

Contenido

1 Enunciado
2 Potencial eléctrico
3 Campo y densidad de carga
4 Presión electrostática
5 Caso práctico

1 Enunciado

Se trata de hallar el campo eléctrico necesario para elevar en el aire una partícula metálica que reposa sobre un plano a tierra. La partícula conductora la podemos modelar como un hemisferio de radio

a

. Existe un campo eléctrico impuesto que, en puntos alejados de la semiesfera, es uniforme y perpendicular al plano conductor,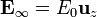 $\mathbf{E}_\infty = E_0\mathbf{u}_{z}$ .

El potencial en todos los puntos por encima del plano y la partícula es de la forma

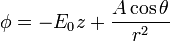
$\phi = -E_0 z + \frac{A\cos\theta}{r^2}$ $(z>0,\ r>a)$

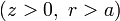
siendo $r$ la distancia al centro de la semiesfera.

Determine el valor de $A$ que hace que se satisfagan todas las ecuaciones y condiciones de contorno.
Halle la densidad de carga en la superficie de la semiesfera.
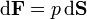Calcule la presión electrostática en la superficie de la partícula. A partir de esta presión, halle la fuerza eléctrica sobre la partícula, empleando la relación $\mathrm{d}\mathbf{F} = p\,\mathrm{d}\mathbf{S}$ .
Si la partícula es de aluminio y su radio vale 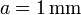$a=1\,\mathrm{mm}$ , ¿qué campo es preciso para levantar esta partícula?

2 Potencial eléctrico

Dado que el espacio por encima del plano y la partícula está vacío, en él el potencial debe verificar la ecuación de Laplace.

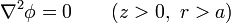
$\nabla^2\phi = 0 \qquad (z>0,\ r>a)$

Como condiciones de contorno, debe cumplir que sobre la superficie del plano de tierra y sobre la semiesfera, el potencial debe anularse

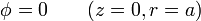
$\phi = 0 \qquad (z=0, r = a)$

mientras que en puntos alejados, el potencial debe reducirse al de un campo uniforme, ya que la partícula no influye en puntos muy alejados

$\phi\to -E_0 z \qquad (r\to\infty)$

El potencial propuesto en el enunciado verifica la ecuación de Laplace por tratarse de la suma del de un campo uniforme con el de un dipolo. En cualquier caso, lo verificamos

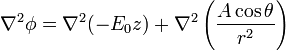
$\nabla^2\phi = \nabla^2(-E_0z) + \nabla^2\left(\frac{A\cos\theta}{r^2}\right)$

Hallando las laplacianos por separado

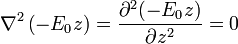
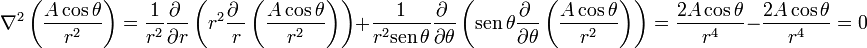
$\nabla^2\left(-E_0z\right) = \frac{\partial^2(-E_0z)}{\partial z^2} = 0$ $\nabla^2\left(\frac{A\cos\theta}{r^2}\right) = \frac{1}{r^2}\frac{\partial \ }{\partial r}\left(r^2\frac{\partial \ }{r}\left(\frac{A\cos\theta}{r^2}\right)\right)+ \frac{1}{r^2\mathrm{sen}\,\theta}\frac{\partial \ }{\partial \theta}\left(\mathrm{sen}\,\theta\frac{\partial\ }{\partial \theta}\left(\frac{A\cos\theta}{r^2}\right)\right)= \frac{2A\cos\theta}{r^4} - \frac{2A\cos\theta}{r^4} = 0$

Vemos que esta ecuación no sirve para determinar $A$ , ya que se satisface sea cual sea su valor.

Aplicando ahora que en la superficie del plano el potencial se anule tenemos que

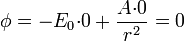
$\phi = -E_0{\cdot}0 + \frac{A{\cdot}0}{r^2} = 0$

ya que en $z = 0$ , $θ = π / 2$ . Esta condición tampoco determina $A$ .

En la superficie de la semiesfera ( $r = a$ ) tenemos

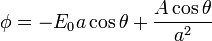
$z = r \cos\theta = a\cos\theta\,$ $\phi = -E_0 a \cos\theta + \frac{A\cos\theta}{a^2}$

para que esta expresión se anule debe ser

A = E 0 a 3

Por último, en el infinito el potencial tiende al de un campo uniforme, ya que el término dipolar tiende a cero.

Resumiendo, la expresión correcta para el potencial es

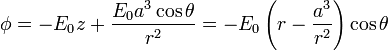
$\phi = -E_0 z + \frac{E_0 a^3\cos\theta}{r^2} = -E_0\left(r-\frac{a^3}{r^2}\right)\cos\theta$

3 Campo y densidad de carga

Conocido el potencial podemos hallar el campo eléctrico y de éste la densidad de carga superficial

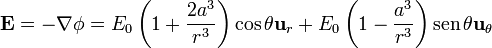
$\mathbf{E} = -\nabla\phi = E_0\left(1+\frac{2a^3}{r^3}\right)\cos\theta\mathbf{u}_{r}+ E_0\left(1-\frac{a^3}{r^3}\right)\mathrm{sen}\,\theta\mathbf{u}_{\theta}$

Justo en la superficie de la partícula este campo se reduce a

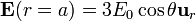
$\mathbf{E}(r=a) = 3E_0 \cos\theta\mathbf{u}_{r}$

Podemos ver que resulta un campo puramente normal a la superficie, como corresponde a un conductor.

La densidad de carga valdrá

$\sigma_s = \varepsilon_0 \mathbf{n}{\cdot}[\mathbf{E}] = \varepsilon_0 \mathbf{u}_{r}{\cdot}\left(3E_0 \cos\theta\mathbf{u}_{r}-\mathbf{0}\right)= 3\varepsilon_0E_0\cos\theta$

Esta densidad de carga es máxima en el polo de la semiesfera y mínima en su ecuador (donde se anula).

4 Presión electrostática

La presión electrostática en la superficie del conductor es

$p = \frac{1}{2}\varepsilon_0 E_n^2 = \frac{9\varepsilon_0 E_0^2\cos^2\theta}{2}$

Esta presión es de nuevo máxima en el polo (donde la densidad de carga es mayor).

Conocida la presión, obtenemos la fuerza diferencial como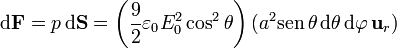 $\mathrm{d}\mathbf{F} = p\,\mathrm{d}\mathbf{S} = \left(\frac{9}{2}\varepsilon_0 E_0^2\cos^2\theta\right)(a^2\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\,\mathbf{u}_{r})$

y la fuerza total será la integral de esta cantidad sobre la semiesfera

$\mathbf{F} =\frac{9}{2}\varepsilon_0 E_0^2 a^2 \int_0^{2\pi}\!\!\!\mathrm{d}\varphi \int_0^{\pi/2}\!\!\!\! \mathrm{d}\theta\,\mathrm{sen}\,\theta\cos^2\theta\mathbf{u}_{r}$

Por tratarse de una integral vectorial, debemos emplear la base cartesiana, para evitar integrar los vectores. Aplicando que

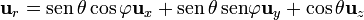
$\mathbf{u}_{r}= \mathrm{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\mathrm{sen}\,\theta\,\mathrm{sen}\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z}$

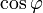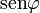y sustituyendo quedan tres integrales. Las dos primeras, $F x$ y $F y$ , se anulan por aparecer en ellas las integrales de $\cos\varphi$ y $\mathrm{sen}\varphi$ en un periodo. Para la tercera

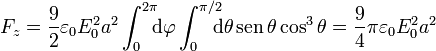
$F_z =\frac{9}{2}\varepsilon_0 E_0^2 a^2 \int_0^{2\pi}\!\!\!\mathrm{d}\varphi \int_0^{\pi/2}\!\!\!\! \mathrm{d}\theta\,\mathrm{sen}\,\theta\cos^3\theta = \frac{9}{4}\pi\varepsilon_0 E_0^2 a^2$

Esta fuerza es proporcional al área de la semiesfera. Es también cuadrática con el campo, ya que resulta de la acción del campo aplicado sobre la carga que él mismo induce. Esto quiere decir que la dirección de la fuerza (hacia arriba) es independiente del sentido del campo aplicado.

5 Caso práctico

Para hallar el campo necesario para levantar la partícula debemos igualar esta fuerza hacia arriba con el peso que va hacia abajo. Cualquier campo superior vencerá al peso y elevará la partícula. Este campo crítico vale

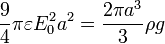
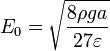
$\frac{9}{4}\pi\varepsilon E_0^2 a^2 = \frac{2\pi a^3}{3} \rho g$ $\Rightarrow$ $E_0 = \sqrt{\frac{8\rho g a}{27\varepsilon}}$

El valor numérico de este campo es

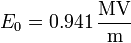
$E_0 = 0.941 \,\frac{\mathrm{MV}}{\mathrm{m}}$

Este campo, aunque intenso, está por debajo del campo de ruptura del aire, lo que indica que es factible levantar partículas milimétricas con un campo eléctrico aplicado.

Fuerza sobre una partícula semiesférica

De Laplace

Contenido

1 Enunciado

2 Potencial eléctrico

3 Campo y densidad de carga

4 Presión electrostática

5 Caso práctico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES