Campo magnético de corrientes estacionarias

De Laplace

Revisión a fecha de 20:02 21 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Fuerza sobre una carga en movimiento
2 Campo magnético debido a una corriente
- 2.1 Aplicaciones
3 Fuentes del campo magnético
4 El potencial vector magnético
5 Dipolo magnético
6 Problemas

1 Fuerza sobre una carga en movimiento

Se ve en electrostática que una carga puntual en reposo experimenta una fuerza 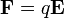$\mathbf{F}=q\mathbf{E}$ . Si esta carga se encuentra en movimiento, debemos añadir una fuerza adicional, proporcional a la velocidad y ortogonal a ella, de acuerdo con la ley de Lorentz

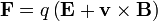
$\mathbf{F} = q\left(\mathbf{E}+\mathbf{v}\times\mathbf{B}\right)$

A esta fuerza adicional se la denomina fuerza magnética, y al campo vectorial $\mathbf{B}$ , que da la magnitud de esta fuerza, se lo denomina campo magnético (también conocido como inducción magnética y como densidad de flujo magnético).

El campo magnético se mide en el SI en Teslas (T), siendo 1 T = 1 N/A·m. Un Tesla es una cantidad grande para los valores usuales, por lo que con frecuencia se usa como unidad el Gauss (1 Gauss = 0.0001 T).

La fuerza sobre una carga en movimiento puede extenderse a un conjunto de ellas, que formarán una densidad de corriente. Para el caso de una densidad 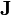$\mathbf{J}$ , la fuerza magnética es

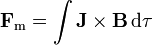
$\mathbf{F}_\mathrm{m}=\int \mathbf{J}\times\mathbf{B}\,\mathrm{d}\tau$

y análogamente se tiene la fuerza sobre una distribución de corriente superficial y sobre un conductor filiforme.

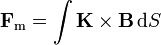
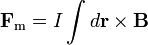
$\mathbf{F}_\mathrm{m}=\int \mathbf{K}\times\mathbf{B}\,\mathrm{d}S$ $\mathbf{F}_\mathrm{m}=I\int d\mathbf{r}\times\mathbf{B}$

Si tenemos un conjunto de distribuciones, la resultante será la suma de la fuerza sobre cada una de ellas.

2 Campo magnético debido a una corriente

Artículo completo: Campo magnético debido a una corriente

Los campos magnéticos pueden tener distintas causas. Entre ellas, se encuentran las propias corrientes eléctricas.

El campo magnético creado por una carga puntual en movimiento a velocidades bajas (comparadas con la de la luz) vale aproximadamente

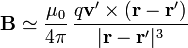
$\mathbf{B}\simeq \frac{\mu_0}{4\pi}\,\frac{q\mathbf{v}'\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}$

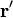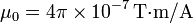siendo $\mathbf{r}'$ la posición instantánea de la carga. $μ 0$ es una constante denominada permeabilidad del vacío, cuyo valor en el SI es $\mu_0=4\pi\times 10^{-7}\,\mathrm{T}{\cdot}\mathrm{m}/\mathrm{A}$ .

El campo magnético creado por una distribución de corriente lineal puede calcularse integrando la expresión anterior. Para el caso de una corriente estacionario la aproximación se convierte en una igualdad y el campo magnético viene dado por la ley de Biot y Savart

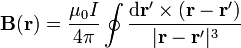
$\mathbf{B}(\mathbf{r})=\frac{\mu_0 I}{4\pi}\oint \frac{\mathrm{d}\mathbf{r}'\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}$

De forma análoga al caso de la corriente lineal tenemos el campo creado por una distribución de corriente estacionaria volumétrica y por una superficial

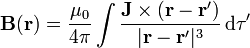
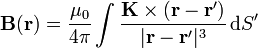
$\mathbf{B}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \frac{\mathbf{J}\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}\tau'$ $\mathbf{B}(\mathbf{r})=\frac{\mu_0}{4\pi}\int \frac{\mathbf{K}\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}S'$

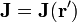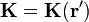En estas expresiones las densidades de corriente son funciones de la posición, $\mathbf{J}=\mathbf{J}(\mathbf{r}')$ , $\mathbf{K}=\mathbf{K}(\mathbf{r}')$ .

2.1 Aplicaciones

Existen muy pocos casos que pueden resolverse de forma sencilla empleando la integración directa de la ley de Biot y Savart.

Un caso particular importante es campo magnético de una corriente rectilínea de longitud finita o infinitamente larga que produce un campo

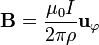
$\mathbf{B} = \frac{\mu_0I}{2\pi\rho}\mathbf{u}_{\varphi}$

Este campo gira en torno al hilo, siendo circunferencias sus líneas de campo

También es importante el campo magnético de una espira circular, que en los puntos de su eje vale

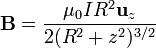
$\mathbf{B} = \frac{\mu_0IR^2\mathbf{u}_{z}}{2(R^2+z^2)^{3/2}}$

Este campo apunta en la dirección del eje de la espira, siendo máximo, con un valor $μ 0 I / 2 R$ en su centro.

3 Fuentes del campo magnético

Al igual que ocurría con el campo eléctrico, el cálculo del campo magnético por integración directa, mediante la ley de Biot y Savart, es complejo incluso en los casos más elementales. Por ello, y porque permite un estudio más profundo, es preferible determinar las fuentes de $\mathbf{B}$ , esto es, calcular sus fuentes escalares (la divergencia de $\mathbf{B}$ ) y sus fuentes vectoriales (el rotacional de $\mathbf{B}$ ), ya que como prueba el teorema de Helmholtz, conocidos la divergencia y el rotacional del un campo, podemos determinar completamente el campo.

3.1 Ley de Gauss para el campo magnético

Artículo completo: Ley de Gauss para el campo magnético

Para las fuentes escalares, tenemos, en forma integral

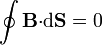
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{S} =0$

y en forma diferencial, aplicando el teorema de Gauss,

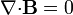
$\nabla{\cdot}\mathbf{B}=0$

En sus dos formas, esta ley expresa la ausencia de fuentes escalares magnéticas, esto es, el campo debido a corrientes eléctricas estacionarias nunca produce el efecto de una carga magnética aislada (monopolo).

Esta ley es aplicable no sólo al caso de corrientes estacionarias, sino que se ha comprobado su validez en cualquier situación, esto es, no se han descubierto monopolos magnéticos.

Asociada a esta ley existe una condición de salto para el campo magnético en una interfaz entre dos regiones

$\mathbf{n}{\cdot}[\mathbf{B}]=0$

que expresa que la componente normal del campo magnético alcanza el mismo valor en sendos lados de una frontera.

3.2 Ley de Ampère

Artículo completo: Ley de Ampère

Tomando el rotacional en la ley de Biot y Savart se obtiene la ley de Ampère en forma diferencial

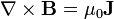
$\nabla\times\mathbf{B} = \mu_0\mathbf{J}$

y, por aplicación del teorema de Stokes, en forma integral

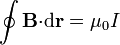
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = \mu_0 I$

que, en palabras, expresa que la circulación del campo magnético de corrientes estacionarias a lo largo de una curva cerrada Γ es igual a la permeabilidad del vacío multiplicada por la corriente total que atraviesa una superficie arbitraria apoyada en Γ y orientada según la regla de la mano derecha.

Asociada a la ley de Ampère se encuentra la condición de salto

$\mathbf{n}\times[\mathbf{B}]=\mu_0\mathbf{K}$

que nos da la discontinuidad en las componentes tangenciales del campo magnético como función de la densidad de corriente superficial.

La ley de Ampère implica que el campo magnético, a diferencia del electrostático, sí tiene fuentes vectoriales, dadas por las densidades de corriente. Geómetricamente, significa que las líneas de campo magnético tenderán a girar alrededor de las líneas de corriente.

3.3 Ecuaciones de la magnetostática

Reuniendo las dos leyes anteriores, podemos describir completamente el comportamiento del campo magnético. Por ello, conjuntamente se denominan las leyes de la magnetostática:

	Diferencial	Salto	Integral
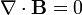
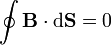
Gauss	$\nabla\cdot\mathbf{B}=0$	$\mathbf{n}\cdot[\mathbf{B}]=0$	$\oint\mathbf{B}\cdot\mathrm{d}\mathbf{S}=0$
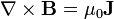
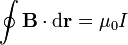
Ampère	$\nabla\times\mathbf{B}=\mu_0\mathbf{J}$	$\mathbf{n}\times[\mathbf{B}]=\mu_0\mathbf{K}$	$\oint\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0I$

3.4 Aplicaciones

Aparte de su esencial importancia teórica, la ley de Ampère (en combinación con la ley de Gauss para el campo magnético) es una poderosa herramienta para el cálculo de campos magnéticos en situaciones de alta simetría.

Así, permite hallar de forma sencilla

El campo magnético de un hilo infinito por el cual circula una corriente $I$

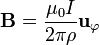
$\mathbf{B}=\frac{\mu_0I}{2\pi\rho}\mathbf{u}_\varphi$

El campo magnético de un cable cilíndrico de radio $a$ por el cual circula una densidad de corriente $J 0$

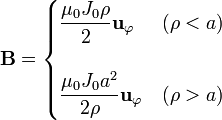
$\mathbf{B}=\begin{cases}\displaystyle\frac{\mu_0J_0\rho}{2}\mathbf{u}_\varphi & (\rho < a) \\ & \\\displaystyle\frac{\mu_0J_0a^2}{2\rho}\mathbf{u}_\varphi & (\rho > a)\end{cases}$

El campo magnético de un solenoide ideal de radio $a$ , con $n$ espiras por unidad de longitud, por las que circula una corriente $I$

4 El potencial vector magnético

Artículo completo: potencial vector magnético

De que el campo magnético sea solenoidal se deduce que puede expresarse como el rotacional de otro campo vectorial, llamado potencial vector magnético

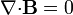
$\nabla{\cdot}\mathbf{B}=0$ $\Rightarrow$ $\mathbf{B} = \nabla\times\mathbf{A}$

El potencial vector de un campo magnético dado no es único, ya que siempre se le puede sumar un gradiente de un campo escalar arbitrario.

Cuando se impone la condición adicional 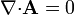$\nabla{\cdot}\mathbf{A} = 0$ , el potencial vector verifica la ecuación de Poisson vectorial

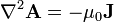
$\nabla^2\mathbf{A} = -\mu_0\mathbf{J}$

entre cuyas soluciones se encuentra

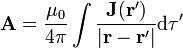
$\mathbf{A} = \frac{\mu_0}{4\pi}\int \frac{\mathbf{J}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'$

con expresiones análogas para corrientes superficiales y lineales.

El potencial vector posee poca utilidad práctica, aunque sí tiene importancia teórica y es útil a la hora de calcular flujos magnéticos, ya que

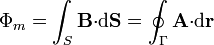
$\Phi_m = \int_S \mathbf{B}{\cdot}\mathrm{d}\mathbf{S} = \oint_\Gamma \mathbf{A}{\cdot}\mathrm{d}\mathbf{r}$

siendo $S$ una superficie apoyada en Γ y orientada según la regla de la mano derecha.

5 Dipolo magnético

Cuando se tiene una distribución de corriente localizada en una pequeña región del espacio, puede aproximarse el campo en puntos alejados de la distribución mediante el \emph{desarrollo multipolar magnético}. Para el caso de una espira cerrada el potencial vector puede aproximarse por

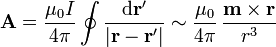
$\mathbf{A} = \frac{\mu_0I}{4\pi}\oint \frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}\sim \frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times \mathbf{r}}{r^3}$

donde 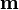$\mathbf{m}$ , el momento magnético dipolar de la distribución es

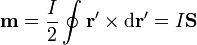
$\mathbf{m}= \frac{I}{2}\oint \mathbf{r}'\times \mathrm{d}\mathbf{r}' = I\mathbf{S}$

Este vector, para una espira lineal plana, tiene por módulo el producto de la corriente que circula por ella por el área delimitada por la curva. Apunta en la dirección normal según la regla de la mano derecha.

Para el caso de una distribución de corriente de volumen o de superficie, la expresión para el potencial vector es idéntica, siendo el momento dipolar

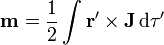
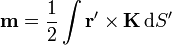
$\mathbf{m} = \frac{1}{2}\int \mathbf{r}'\times \mathbf{J}\,\mathrm{d}\tau'$ $\mathbf{m} = \frac{1}{2}\int \mathbf{r}'\times \mathbf{K}\,\mathrm{d}S'$

En ocasiones, 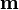$\mathbf{m}$ es nulo para una distribución dada, lo que obliga a recurrir a términos de orden superior en el desarrollo multipolar (término cuadrupolar, octupolar,…).

A partir del potencial vector de un dipolo puede hallarse el campo magnético, que resulta ser análogo al campo eléctrico de un dipolo $\mathbf{p}$

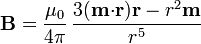
$\mathbf{B}=\frac{\mu_0}{4\pi}\,\frac{3(\mathbf{m}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}$

Cuando un dipolo magnético 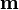$\mathbf{m}$ se encuentra sometido a la acción de un campo magnético externo, experimenta una fuerza

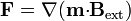
$\mathbf{F}= \nabla(\mathbf{m}{\cdot}\mathbf{B}_\mathrm{ext})$

y un momento de la fuerza

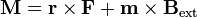
$\mathbf{M}=\mathbf{r}\times\mathbf{F} + \mathbf{m}\times\mathbf{B}_\mathrm{ext}$

El segundo término representa un par intrínseco que tiende a alinear el dipolo con el campo magnético, lo que constituye el fundamento de las brújulas. Estas dos interacciones pueden derivarse de la energía de un dipolo en un campo externo

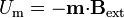
$U_\mathrm{m}=-\mathbf{m}{\cdot}\mathbf{B}_\mathrm{ext}$

Esta energía es mínima cuando el dipolo apunta en la misma dirección y sentido que el campo aplicado sobre él.

6 Problemas

Artículo completo: Problemas de campo magnético de corrientes estacionarias

Campo magnético de corrientes estacionarias

De Laplace

Contenido

1 Fuerza sobre una carga en movimiento

2 Campo magnético debido a una corriente

2.1 Aplicaciones

3 Fuentes del campo magnético

3.1 Ley de Gauss para el campo magnético

3.2 Ley de Ampère

3.3 Ecuaciones de la magnetostática

3.4 Aplicaciones

4 El potencial vector magnético

5 Dipolo magnético

6 Problemas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES