Movimiento de una carga en un campo magnético uniforme

De Laplace

Contenido

1 Enunciado
2 Introducción
3 Caso de una velocidad inicial paralela al campo magnético
4 Caso de una velocidad inicial perpendicular al campo magnético
5 Caso de una velocidad inicial arbitraria

1 Enunciado

Una partícula de masa $m$ y carga $q$ se mueve en el interior de un campo magnético uniforme 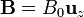$\mathbf{B}=B_0\mathbf{u}_{z}$ . Si la partícula se halla inicialmente en el origen y moviéndose con velocidad 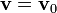$\mathbf{v}=\mathbf{v}_0$ . ¿Cuál es la trayectoria posterior? ¿Cuál es la posición en un instante de tiempo $t$ ?

2 Introducción

Este problema trata simplemente de aplicar la segunda ley de Newton 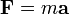$\mathbf{F}=m\mathbf{a}$ , a la ley de Lorentz

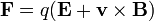
$\mathbf{F}=q(\mathbf{E}+\mathbf{v}\times\mathbf{B})$

Si sólo tenemos presente un campo magnético la ecuación de movimiento a resolver se reduce a

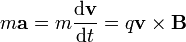
$m\mathbf{a}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=q\mathbf{v}\times\mathbf{B}$

Para resolver esta ecuación consideraremos en primer lugar dos casos particulares:

3 Caso de una velocidad inicial paralela al campo magnético

Si la velocidad inicial es paralela al campo magnético, la fuerza en el instante inicial es

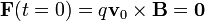
$\mathbf{F}(t=0)=q \mathbf{v}_0\times\mathbf{B}=\mathbf{0}$

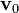Por tanto, la aceleración inicial es nula y $\mathbf{v}$ un instante posterior seguirá siendo $\mathbf{v}_0$ . Extendiendo este razonamiento a todos los instantes posteriores resulta

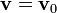
$\mathbf{v}=\mathbf{v}_0\,$

esto es, si la velocidad inicial es paralela a $\mathbf{B}$ , esta velocidad permanece constante. La partícula describe un movimiento rectilíneo y uniforme paralelamente al campo magnético. La posición en un instante cualquiera será

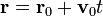
$\mathbf{r}=\mathbf{r}_0+\mathbf{v}_0 t\,$

4 Caso de una velocidad inicial perpendicular al campo magnético

Si la velocidad inicial es perpendicular al campo magnético, la fuerza inicial no será nula

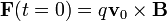
$\mathbf{F}(t=0)=q \mathbf{v}_0\times\mathbf{B}$

Sin embargo, por ser un producto vectorial en el que interviene $\mathbf{B}$ , resulta una aceleración perpendicular al campo magnético. Esto hace que la velocidad en un instante posterior

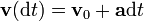
$\mathbf{v}(\mathrm{d}t)=\mathbf{v}_0+\mathbf{a}\mathrm{d}t\,$

sea también perpendicular al campo magnético. Extendiendo el razonamiento, resulta que si la velocidad inicial es perpendicular al campo magnético, lo será en todo instante.

La partícula se mueve sobre un plano perpendicular al campo magnético.

Queda determinar el movimiento sobre dicho plano. Si descomponemos la aceleración en sus componentes normal y tangencial

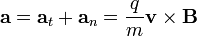
$\mathbf{a}=\mathbf{a}_t+\mathbf{a}_n=\frac{q}{m}\mathbf{v}\times\mathbf{B}$

La aceleración tangencial es la componente paralela a la velocidad, pero el segundo miembro es puramente normal a ella, por tanto

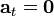
$\mathbf{a}_t=\mathbf{0}$

Ello implica que

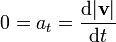
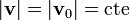
$0=a_t=\frac{\mathrm{d}|\mathbf{v}|}{\mathrm{d}t}$ $\Rightarrow$ $|\mathbf{v}|=|\mathbf{v}_0|=\mathrm{cte}$

Por ser la fuerza de Lorentz puramente normal, la partícula se mueve con velocidad de módulo constante. Este resultado es general en cuanto a que no depende de si el campo magnético es uniforme o no. También puede expresarse en términos de la energía cinética

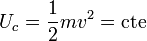
$U_c=\frac{1}{2}mv^2=\mathrm{cte}$

La energía cinética de una carga en un campo magnético permanece constante. El campo magnético no realiza trabajo sobre ella.

Yendo ahora a la aceleración normal, su módulo es

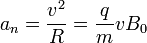
$a_n=\frac{v^2}{R}=\frac{q}{m}vB_0$

De aquí se deduce que la partícula se mueve con radio de curvatura constante

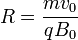
$R=\frac{mv_0}{qB_0}$

Una trayectoria plana de radio constante es una circunferencia. El radio de esta circunferencia se denomina radio de Larmor.

La frecuencia de giro es independiente de la velocidad inicial

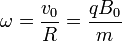
$\omega=\frac{v_0}{R}=\frac{qB_0}{m}$

Esta cantidad (conocida como frecuencia ciclotrón) permite identificar las partículas en los detectores de los aceleradores de partículas, donde estas trayectorias se observan habitualmente.

5 Caso de una velocidad inicial arbitraria

Supongamos ahora que la velocidad inicial no es ni paralela ni perpendicular a $\mathbf{B}$ , sino que forma un cierto ángulo $α$ con el campo magnético. En este caso, podemos descomponer el problema en suma de los dos casos anteriores. Para ello, escribimos la velocidad como una superposición de una velocidad paralela a $\mathbf{B}$ (proyectando sobre esta dirección) y otra perpendicular (hallando el complementario)

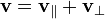
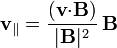
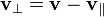
$\mathbf{v}=\mathbf{v}_\parallel+\mathbf{v}_\perp$ $\mathbf{v}_\parallel=\frac{(\mathbf{v}{\cdot}\mathbf{B})}{|\mathbf{B}|^2}\,\mathbf{B}$ $\mathbf{v}_\perp=\mathbf{v}-\mathbf{v}_\parallel$

La fuerza de Lorentz, en términos de estas dos componentes, es

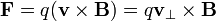
$\mathbf{F}=q(\mathbf{v}\times\mathbf{B})=q\mathbf{v}_\perp \times\mathbf{B}$

ya que el producto de dos vectores paralelos se anula. La fuerza resultante es también perpendicular a $\mathbf{B}$ . Por tanto

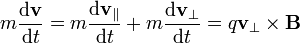
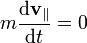
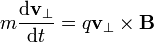
$m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=m\frac{\mathrm{d}\mathbf{v}_\parallel}{\mathrm{d}t}+m\frac{\mathrm{d}\mathbf{v}_\perp}{\mathrm{d}t}=q\mathbf{v}_\perp\times\mathbf{B}$ $\Rightarrow$ $m\frac{\mathrm{d}\mathbf{v}_\parallel}{\mathrm{d}t}=0$ $m\frac{\mathrm{d}\mathbf{v}_\perp}{\mathrm{d}t}=q\mathbf{v}_\perp\times\mathbf{B}$

El resultado final es una combinación de los que ya hemos visto: el movimiento paralelo al campo magnético es uniforme, mientras que el perpendicular es circular. La combinación de estos dos movimientos es uno helicoidal. El radio de esta hélice es

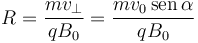
$R=\frac{mv_\perp}{q B_0}=\frac{mv_0\,\mathrm{sen}\,\alpha}{qB_0}$

mientras que el paso de rosca (altura que sube al dar una vuelta) es

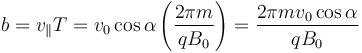
$b=v_\parallel T=v_0\cos\alpha\left(\frac{2\pi m}{q B_0}\right)=\frac{2\pi m v_0\cos\alpha}{q B_0}$

El sentido con el que se recorre la hélice depende del signo de la carga.

Movimiento de una carga en un campo magnético uniforme

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Caso de una velocidad inicial paralela al campo magnético

4 Caso de una velocidad inicial perpendicular al campo magnético

5 Caso de una velocidad inicial arbitraria

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES