Fuerza sobre una espira inmersa parcialmente en un campo magnético
De Laplace
1 Enunciado
Una espira plana de forma irregular se coloca de forma que parte de ella se encuentra en un campo magnético uniforme 
(en la figura el campo ocupa la región sombreada y apunta perpendicularmente al plano de la espira). Por la espira circula una corriente I. Pruebe que la fuerza magnética neta sobre la espira es F = IBs, donde s es la cuerda subtendida.
Generalice este resultado para el caso de que la forma de la región ocupada por el campo magnético sea también irregular. ¿En qué dirección apunta la fuerza?
2 Solución
La fuerza sobre una espira por la cual circula una corriente I viene dada por la integral
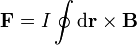
En nuestro caso, el campo tiene un valor uniforme igual a cero en una región y es también uniforme y vale 
en otra. Esto permite separar la integral en dos tramos
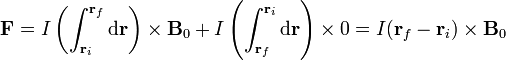
Dado el sentido de recorrido de la curva, se tiene que
por lo que
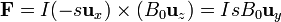
como queríamos demostrar.
Si la región ocupada por el campo magnético es asimismo irregular, el razonamiento es análogo. La fuerza sigue siendo
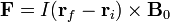
Si definimos un vector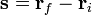 
resulta
que, en módulo, sigue valiendo IsB0, y que tiene por dirección la perpendicular a los vectores 
y . Este resultado, como se ve, no depende en absoluto de la forma concreta de la espira, sólo de la distancia entre los dos puntos en que toca la frontera. Si la corriente y el campo verifican la regla de la mano derecha, la fuerza es tal que la espira tiende a ir a la región de campo más intenso.
