Fuerza entre un hilo y un dipolo magnético

De Laplace

1 Enunciado

Por un cable vertical muy largo, se hace circular una corriente $I 0$ . Un pequeño imán (equivalente a un dipolo magnético 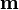$\mathbf{m}$ ), de peso $M\mathbf{g}$ , se suspende de un hilo ideal, de longitud $l$ , cuyo punto de sujeción se encuentra a una distancia $a$ del cable. El imán está sujeto por su punto central, de forma que puede orientarse libremente. ¿En que dirección apuntará el imán? Calcule la fuerza magnética sobre el imán, cuando se encuentra a una distancia $x$ del cable. Halle la ecuación para el ángulo que el hilo forma con la vertical.

2 Solución

El dipolo magnético se orientará en la misma dirección y sentido que el campo magnético, en el punto en que se encuentre.

El campo del hilo, en cilíndricas, es

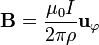
$\mathbf{B}=\frac{\mu_0 I}{2\pi \rho}\mathbf{u}_{\varphi}$

de forma que el dipolo apunta en la dirección de 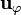$\mathbf{u}_{\varphi}$ . Para hallar la fuerza debemos calcular

$\mathbf{F}=\left(\mathbf{m}{\cdot}\nabla\right)\mathbf{B}$

El operador del paréntesis es

$\mathbf{m}{\cdot}\nabla=\left(m\mathbf{u}_{\varphi}\right){\cdot}\left(\mathbf{u}_{\rho}\frac{\partial{}\ }{\partial{}\rho}+ \frac{\mathbf{u}_{\varphi}}{\rho}\,\frac{\partial{}\ }{\partial{}\varphi}+ \mathbf{u}_{z}\,\frac{\partial{}\ }{\partial{}z}\right)=\frac{m}{\rho}\,\frac{\partial{}\ }{\partial{}\varphi}$

La fuerza es entonces

$\mathbf{F}=\frac{m}{\rho}\,\frac{\partial{}\ }{\partial{}\varphi}\left(\frac{\mu_0 I}{2\pi \rho}\mathbf{u}_{\varphi}\right)$

La única dependencia con $\varphi$ se encuentra justamente en el vector de la base. Se tiene

$\frac{\partial{}\mathbf{u}_{\varphi}}{\partial{}\varphi}=-\mathbf{u}_{\rho}$

Para llegar a este resultado, basta recordar las expresiones

$\mathbf{u}_{\rho}=\cos\varphi\mathbf{u}_{x}+\,\mathrm{sen}\,\varphi\mathbf{u}_{y}$ $\mathbf{u}_{\varphi}=-\,\mathrm{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y}$

De aquí resulta, para la fuerza