Campo de un solenoide cilíndrico
De Laplace
Contenido |
1 Enunciado
Un solenoide de radio a, altura h y n espiras por unidad de longitud, puede aproximarse por una distribución de corriente superficial sobre un cilindro.
- Halle el valor
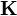 equivalente a que por las espiras circule una corriente I.
equivalente a que por las espiras circule una corriente I.
- Empleando las leyes de la magnetostática, calcule el campo producido por el solenoide, si
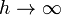 .
.
- Mediante integración directa, halle el campo magnético en los puntos del eje del cilindro si h es finito.
- Estudie el límite
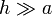
- Compare los valores del campo en el centro del solenoide y justo en el borde de él. Considere los límites de una espira circular (
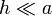 y de un solenoide infinito
y de un solenoide infinito 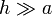 )
)
- Estudie el límite
2 Densidad superficial de corriente
Dada una densidad de corriente superficial, la relación entre ésta y la intensidad de corriente total que atraviesa una línea trazada en la superficie es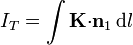
donde 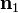 es un vector unitario normal a la curva y tangente a la superficie.
es un vector unitario normal a la curva y tangente a la superficie.
Para establecer la correspondencia entre la corriente que circula por el solenoide y la densidad de corriente equivalente, imponemos que sea idéntica la corriente total que atraviesa una línea vertical trazada sobre el solenoide. Esta línea corta N espiras, siendo
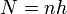
por lo que la corriente total que atraviesa la línea es
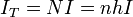
con I la intensidad que circula por cada espira. Si se supone una densidad de corriente superficial 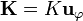 resulta
resulta

Igualando ambas cantidades se tiene la relación
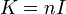
o, equivalentemente K = NI / h.
3 Campo en un solenoide infinito
Si la longitud del solenoide es muy grande comparada con su radio, podemos hacer la aproximación de un cilindro infinito, sobre el cual circula una corriente 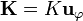 .
.
El campo magnético de este solenoide ideal tiene, en principio, tres componentes
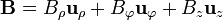
Dada la simetría del sistema, estas componentes serán independientes tanto de la coordenada z (el sistema no cambia en una traslación a lo largo del cilindro), como de la coordenada  (el sistema no cambia en una rotación). Las tres coordenadas sólo pueden depender de la coordenada ρ.
(el sistema no cambia en una rotación). Las tres coordenadas sólo pueden depender de la coordenada ρ.
Teniendo esto en cuenta, podemos simplificar las ecuaciones diferenciales de la magnetostática. Si denominamos región 1 al interior del cilindro y 2 a la exterior, tanto en una región como en la otra, la ley de Gauss para el campo magnético queda
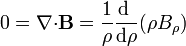
por lo que

Sin embargo, el campo magnético no puede ser infinito en el el eje del cilindro, en el que no hay ninguna densidad de corriente, por lo que
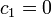
Por otra parte, la condición de continuidad en la componente radial del campo sobre la superficie del cilindro implica
![0=\mathbf{n}{\cdot}[\mathbf{B}]=B_{2\rho}-B_{1\rho}](/wiki/images/math/8/d/f/8dffa0e39d5f73f8dc8ce0d7df633057.png)

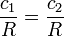

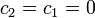
Se deduce entonces que la componente radial es nula en todos los puntos del espacio. Este resultado puede también deducirse de la ley de Gauss en forma integral. Si la componente radial fuera no nula habría un flujo distinto de cero en una superficie que rodeara al cilindro. Una situación similar se produce en el caso de un hilo infinito.
Para las componentes acimutal, 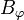 , y longitudinal Bz, tenemos la ley de Ampère, que, teniendo en cuenta las simetrías, se reduce a
, y longitudinal Bz, tenemos la ley de Ampère, que, teniendo en cuenta las simetrías, se reduce a
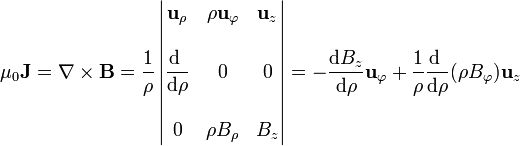
El producto 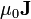 se anula tanto dentro como fuera del cilindro, por lo que, en cada región
se anula tanto dentro como fuera del cilindro, por lo que, en cada región
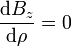

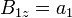
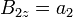
y, de la otra componente
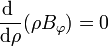

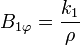
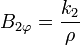
Ahora bien, en el eje del cilindro, en el cual no hay corriente alguna, el campo no puede hacerse infinito, por lo que
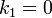
Por otra parte, el campo debe anularse en el infinito,, con lo que
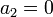
Las dos constantes que quedan se determinan a partir de las condiciones de salto para las componentes tangenciales
![\mathbf{n}\times[\mathbf{B}]=\mathbf{u}_{\rho}\times\left(\left(\frac{k_2}{R}\mathbf{u}_{\varphi}\right)-\left(a_1\mathbf{u}_{z}\right)\right)= \frac{k_2}{R}\mathbf{u}_{z}+a_1\mathbf{u}_{\varphi}](/wiki/images/math/d/3/7/d37ec89196d02a26fe446831512ad691.png)
Esta cantidad debe ser igual a 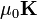 , por lo que
, por lo que

 k2 = 0 a1 = μ0K
k2 = 0 a1 = μ0KEl resultado final es que en el exterior del solenoide no hay campo magnético

mientras que en el interior, el campo es uniforme
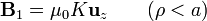
o, en términos de la corriente que circula por las espiras
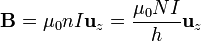
Puede demostrarse, empleando la ley de Biot y Savart, que este resultado es válido para cualquier solenoide, no necesariamente
circular. Siempre que se tenga una superficie que se extiende indefinidamente en la dirección del eje Z, sobre la cual fluye una
corriente de módulo uniforme y dirección perpendicular al eje Z, resulta un campo magnético nulo en el exterior y uniforme e igual a 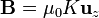 en el interior.
en el interior.
4 Campo en un solenoide finito
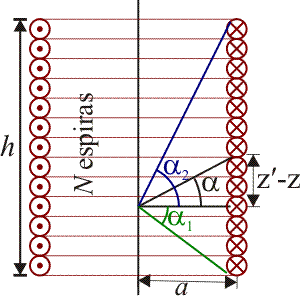
El campo en los puntos del eje puede aproximarse a partir de la superposición del campo de N espiras, situada cada una a una altura zi. El campo debido a cada una de estas espiras va en la dirección del eje Z y depende de la altura como una función en forma de campana.
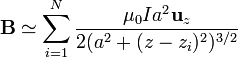
Esta expresión es aproximada porque sustituye lo que en realidad es una hélice por un conjunto de espiras circulares desconectadas entre sí.
La distancia Δz' entre dos espiras sucesivas es aproximadamente la inversa de la densidad (cuando N es grande), ya que
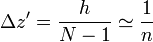
En el caso de un solenoide densamente arrollado esta distancia equivale al diámetro del hilo, ya que no quedan intersticios entre vueltas sucesivas.
Esto nos permite expresar el sumatorio como
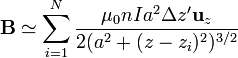
pero nI = K es la densidad de corriente superficial equivalente. Por otra parte, podemos escribir el sumatorio en términos de z' = zi, en vez de i, lo que nos deja el sumatorio como
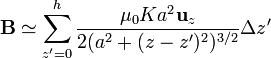
y, teniendo en cuenta que Δz' es una cantidad muy pequeña, comparada con la longitud de la bobina, podemos aproximar el sumatorio por una integral
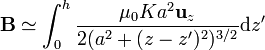
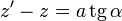
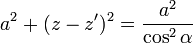
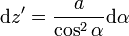
En este caso, α representa la elevación con la que se ve un punto del solenoide, visto desde un punto del eje. Este cambio de variable transforma la integral en
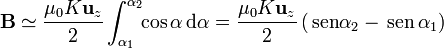
con α1 y α2 los ángulos con los que se ven los extremos del solenoide.
4.1 Dependencia con la posición
La forma del campo, como función de z posee aspecto de “meseta” que se reduce a una campana en el límite 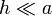 (en el cual el solenoide se reduce a una espira), mientras que en el límite
(en el cual el solenoide se reduce a una espira), mientras que en el límite 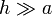 el campo tiende a un valor constante en el interior de la bobina.
el campo tiende a un valor constante en el interior de la bobina.
| 
|
| Escalado con el radio | Escalado con la longitud |
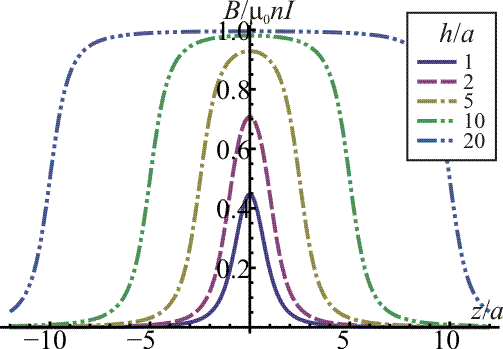
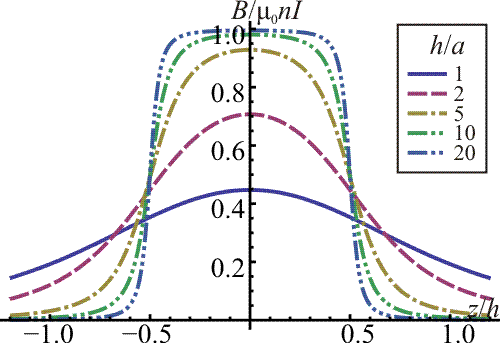
- En la gráfica de la izquierda vemos como varía el comportamiento con la longitud, para un radio fijado. A medida que aumenta h la curva se va aplanando y va tendiendo al valor límite del solenoide infinito.
- En la gráfica de la derecha aparece la variación en el comportamiento variando el radio, para una longitud fijada. A medida que el radio se va reduciendo la curva va tendiendo a una mesa, que cae bruscamente en los extremos del solenoide. El campo es prácticamente nulo fuera del solenoide.
4.2 El límite de un solenoide infinito
En el caso de un solenoide con una longitud mucho mayor que su radio 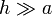 , los ángulos tienen los límites
, los ángulos tienen los límites
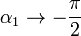
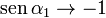
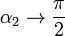
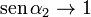
y el resultado se reduce al obtenido en el apartado anterior
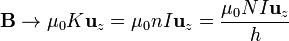
con la diferencia de que en el apartado anterior demostramos que este resultado era cierto no sólo en los puntos del eje, sino en todos los puntos del interior del solenoide.
4.3 Campo en el centro y en el borde
4.3.1 En el centro
Si consideramos el punto central del interior del solenoide, tenemos que
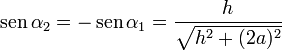
y el campo adopta la expresión sencilla
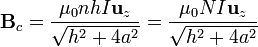
Para este punto es fácil tomar los dos límites indicados anteriormente
- El solenoide se reduce a una espira circular cuando N = 1 y
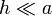 , quedando
, quedando
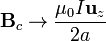
- El solenoide se puede considerar infinito suponiendo n finito y
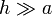
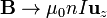
4.3.2 En el borde
En el punto del eje situado justo a la altura del borde del solenoide
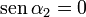
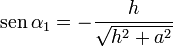
y el campo vale
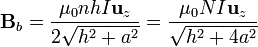
En los dos límites considerados:
- Si el solenoide se reduce a una espira circular (N = 1 y
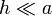 )
)
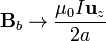
- que es el mismo valor que en el centro.
- Sl solenoide se puede considerar infinito (n finito y
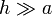 )
)
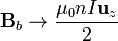
- que es la mitad del campo en el centro
Más en general, dividiendo el módulo del campo en el borde por el del campo en el centro obtenemos la proporción
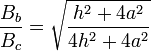
que muestra que el campo en el borde es siempre menor que en el centro, siendo ambos coincidentes cuando 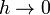 y el uno la mitad del otro si
y el uno la mitad del otro si 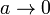 .
.