Problemas de campo magnético de corrientes estacionarias
De Laplace
1  Movimiento de una carga en un campo magnético uniforme
Movimiento de una carga en un campo magnético uniforme
Una partícula de masa m y carga q se mueve en el interior de un campo magnético uniforme 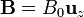 . Si la partícula se halla inicialmente en el origen y moviéndose con velocidad
. Si la partícula se halla inicialmente en el origen y moviéndose con velocidad 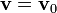 . ¿Cuál es la trayectoria posterior? ¿Cuál es la posición en un instante de tiempo t?
. ¿Cuál es la trayectoria posterior? ¿Cuál es la posición en un instante de tiempo t?
2  Movimiento en el campo de un dipolo
Movimiento en el campo de un dipolo
Una carga puntual q se mueve en el interior del campo de un dipolo magnético 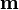 . Inicialmente (en
. Inicialmente (en 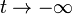 la carga se encuentra en el plano perpendicular al dipolo, muy alejada del éste y moviéndose en línea recta hacia el dipolo.
la carga se encuentra en el plano perpendicular al dipolo, muy alejada del éste y moviéndose en línea recta hacia el dipolo.
- Demuestre que la carga se mantiene en todo momento en el plano perpendicular al dipolo.
- Escriba las ecuaciones de movimiento para la carga.
- Demueste que la energía cinética de la carga permanece constante.
- Demuestre que la carga se acerca a una distancia mínima del dipolo y a partir de ahí vuelve a alejarse. Determine el ángulo entre las direcciones con la que se acerca y se aleja.
3  Fuerza entre dos cargas en movimiento
Fuerza entre dos cargas en movimiento
Dos cargas puntuales iguales + q se mueven con la misma celeridad v de forma que en un instante se encuentran situadas en 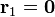 y
y 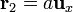 , respectivamente.
, respectivamente.
Si las dos cargas se mueven con velocidades pequeñas 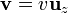 , calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra. ¿Cuál es la proporción entre estas dos fuerzas?
, calcule el valor aproximado de la fuerza eléctrica y de la fuerza magnética que ejerce cada carga sobre la otra. ¿Cuál es la proporción entre estas dos fuerzas?
¿Cómo cambian estas fuerzas si se cambia el signo de una de las cargas, el sentido de una de las velocidades, o ambas cosas a la vez?
Calcule el valor de estas fuerzas si 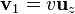 ,
, 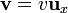 . ¿Se verifica la tercera ley de Newton?
. ¿Se verifica la tercera ley de Newton?
4  Fuerza sobre una espira inmersa parcialmente en un campo magnético
Fuerza sobre una espira inmersa parcialmente en un campo magnético
Una espira plana de forma irregular se coloca de forma que parte de ella se encuentra en un campo magnético uniforme  (en la figura el campo ocupa la región sombreada y apunta perpendicularmente al plano de la espira). Por la espira circula una corriente I. Pruebe que la fuerza magnética neta sobre la espira es F = IBs, donde s es la cuerda subtendida.
(en la figura el campo ocupa la región sombreada y apunta perpendicularmente al plano de la espira). Por la espira circula una corriente I. Pruebe que la fuerza magnética neta sobre la espira es F = IBs, donde s es la cuerda subtendida.
Generalice este resultado para el caso de que la forma de la región ocupada por el campo magnético sea también irregular. ¿En qué dirección apunta la fuerza?
5  Fuerza magnética sobre un dipolo eléctrico
Fuerza magnética sobre un dipolo eléctrico
Un dipolo eléctrico, que puede suponerse formado por dos cargas puntuales 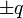 situadas en los extremos de una varilla corta, de longitud L = p / q, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro,
situadas en los extremos de una varilla corta, de longitud L = p / q, se mueve en el interior de un campo magnético. El movimiento del dipolo puede describirse mediante la velocidad de su centro,  , y la velocidad angular con la que gira en torno a él,
, y la velocidad angular con la que gira en torno a él,  .
.
- Calcule la fuerza que el campo magnético ejerce sobre el dipolo.
- Halle el momento de la fuerza producido por el campo.
6  Campo magnético de una corriente rectilínea
Campo magnético de una corriente rectilínea
Halle, por integración directa, el campo magnético producido en todo el espacio por un segmento rectilíneo de longitud L por el cual circula una corriente continua I.
A partir del resultado anterior, halle el campo producido en todos los puntos del espacio por un hilo de longitud infinita por el cual circula una corriente continua I.
Para el caso de un hilo infinito, determine este mismo campo magnético partiendo de las ecuaciones de la magnetostática.
7  Campo producido por una espira poligonal
Campo producido por una espira poligonal
Por las espira de formas irregulares de las figuras circula una corriente I. Halle el valor del campo en el punto P en cada caso.
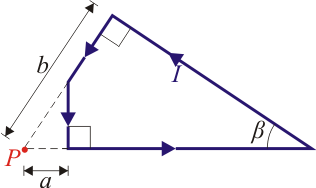
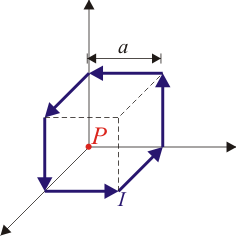
Para cada una de las espiras, hállese su momento magnético y la expresión del campo magnético y del potencial vector en puntos alejados de la espira.
8  Campo magnético de una espira rectangular
Campo magnético de una espira rectangular
Suponga una espira rectangular de lados a y b, por la cual circula una corriente continua I.
- Halle el campo magnético en el centro de la espira. ¿A qué se reduce el resultado si a = b? ¿Y si
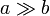 ?
?
Para el caso de una espira de lados 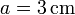 ,
, 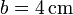 por la que circula una corriente
por la que circula una corriente 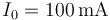
- Halle el campo exacto en el centro de la espira.
- Empleando la aproximación dipolar, calcule el campo a una distancia de
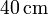 del centro, en el eje de la espira.
del centro, en el eje de la espira. - A una distancia de
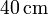 del centro, a lo largo de una diagonal de la espira.
del centro, a lo largo de una diagonal de la espira.
9  Campo magnético de tres hilos
Campo magnético de tres hilos
Una línea de alta tensión trifásica está formada por tres hilos paralelos coplanarios, separados una distancia a, por los cuales circulan las corrientes
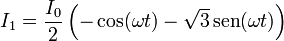
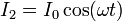
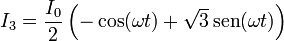
siendo ω la frecuencia de oscilación, que se considera muy baja.
- Calcule la circulación, como función del tiempo, del campo magnético
 a lo largo de un contorno rectangular de base 3a y altura a perpendicular al plano de los hilos y que rodea a los tres.
a lo largo de un contorno rectangular de base 3a y altura a perpendicular al plano de los hilos y que rodea a los tres.
- Calcule el valor del campo magnético en el plano de los hilos.
- Halle la fuerza sobre un segmento de longitud h del hilo central, como función del tiempo. ¿Cuánto vale la fuerza máxima? Calcule su valor numérico para el caso a = 1 m, h = 1 m,
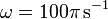 , I0 = 2 kA.
, I0 = 2 kA.
10  Fuerza entre un hilo y una espira
Fuerza entre un hilo y una espira
Una espira rectangular de lados a y b, recorrida por una corriente I1, es coplanaria con un conductor rectilíneo, por el que circula una corriente I2. La distancia del centro de la espira al hilo es d. Halle la fuerza que aparece entre el hilo y la espira.
11  Pequeña espira junto a hilo
Pequeña espira junto a hilo
Un conductor cilíndrico de radio muy pequeño a y longitud indefinida es recorrido por una corriente continua I0. Una espira cuadrada muy pequeña, de lado b, resistencia R y autoinducción despreciable, es coplanaria con el hilo y se encuentra situada a una distancia y de éste (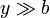 ).
).
- Calcule, detallando los pasos, el campo magnético producido por el hilo en su exterior
- Si por la espira circula una corriente I1, ¿qué fuerza ejerce el hilo sobre ella?
- Suponga que la espira se aleja del hilo, sin cambiar su orientación, de modo que y = y0 + v0t, ¿cuánto vale la corriente I1 inducida en la espira en un instante t? ¿Y la fuerza que el hilo ejerce sobre ella?
12  Campo magnético de una espira circular
Campo magnético de una espira circular
Halle el campo magnético en todos los puntos del eje de una espira circular de radio a por la cual circula una corriente continua I.
13 Campo magnético de una esfera rotatoria
Una esfera de radio a almacena una carga Q distribuida uniformemente en su superficie. La esfera gira con velocidad angular ω alrededor de un eje.
-
 Determine la densidad de corriente en la esfera
Determine la densidad de corriente en la esfera
-
 Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
-
 Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
-
 Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
14  Cálculo de las fuentes de un campo magnético
Cálculo de las fuentes de un campo magnético
En el espacio alrededor de una esfera superconductora existe un campo magnético de la forma

- Calcule los valores de las constantes C1 y C2.
- Determine las corrientes que crean este campo.
- ¿A qué tiende este campo para
 ?
?
- Este campo puede escribirse como el del apartado anterior, más el campo de un dipolo magnético. ¿Cuánto vale su momento dipolar magnético?
15  Campo de dos anillos coplanarios
Campo de dos anillos coplanarios
En el plano z = 0 se encuentran dos anillos coplanarios concéntricos, de radios a y b (b > a). Por el anillo interior circula una corriente I0.
- Halle la corriente I1 que debe circular por el anillo exterior para que el campo magnético en el centro de los anillos se anule.
- Calcule el campo magnético en todos los puntos del eje del sistema.
- Halle el campo en todos los puntos del espacio alejados de los anillos.
- Suponga que b = 2a y que nos situamos a una altura z = 10a. ¿Cuál es el error relativo cometido al aproximar el valor exacto del campo por la aproximación dipolar?
16  Campo de un solenoide cilíndrico
Campo de un solenoide cilíndrico
Un solenoide de radio a, altura h y n espiras por unidad de longitud, puede aproximarse por una distribución de corriente superficial sobre un cilindro.
- Halle el valor
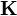 equivalente a que por las espiras circule una corriente I.
equivalente a que por las espiras circule una corriente I.
- Empleando las leyes de la magnetostática, calcule el campo producido por el solenoide, si
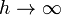 .
.
- Mediante integración directa, halle el campo magnético en los puntos del eje del cilindro si h es finito. Estudie el límite
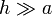
17  Construcción de una bobina
Construcción de una bobina
Se dispone de una bobina de 26 mm de diámetro y 300 vueltas, construida con un hilo de cobre de sección circular de 0.5 mm de diámetro que se enrolla dejando un espacio de 0.1 mm entre vuelta y vuelta.
- Calcule la resistencia de la bobina, el voltaje que hay que aplicar entre los extremos para que circule por ella una corriente de 0.5 A y el calor generado por segundo en ella por efecto Joule.
- Halle el valor aproximado del campo magnético que se produce en el interior de la bobina para esta corriente, así como el de la energía magnética almacenada en ella.
- Calcule el coeficiente de autoinducción de la bobina.
- Suponga que se cortocircuita la fuente, ¿cuánto tiempo tarda aproximadamente en desaparecer la corriente que circula por la bobina?
18  Campo de un tubo cilíndrico
Campo de un tubo cilíndrico
Sobre un cilindro de radio a y longitud infinita fluye una corriente superficial de densidad uniforme 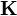 . Halle el campo magnético en todos los puntos del espacio.
. Halle el campo magnético en todos los puntos del espacio.
19  Campo magnético de un cable cilíndrico
Campo magnético de un cable cilíndrico
Calcule el campo magnético producido en todo el espacio por un cable cilíndrico de radio a y longitud infinita, por el cual circula una densidad de corriente uniforme  en la dirección de su eje.
en la dirección de su eje.
20  Corriente y campo de un cable coaxial
Corriente y campo de un cable coaxial
Se tiene un cable coaxial rectilíneo de longitud L = 20 m formado por un núcleo cilíndrico de cobre de radio a = 4 mm, rodeado de una capa de dieléctrico ideal de radio exterior b = 7 mm. Por fuera del dieléctrico se encuentra una corona, también de cobre, de radio exterior c = 9 mm. El cable está terminado en un cortocircuito que conecta el núcleo interior con la corona exterior. En el extremo inicial del cable se establece una diferencia de potencial V0 = 3 mV.
- Calcule la intensidad de corriente que circula por el núcleo de cobre, así como la densidad de corriente y el campo eléctrico en todos los puntos del cobre.
- Calcule el valor aproximado del campo magnético B en todos los puntos del espacio. Suponga que μ = μ0 en todos los materiales. Desprecie los efectos de borde, considerando, para el cálculo de $\mathbf{B}$, el cable como de longitud infinita.
21  Corriente en el interior de una tubería
Corriente en el interior de una tubería
Por el interior de una tubería cilíndrica de radio a fluye un líquido con una velocidad, dependiente de la distancia al eje, ρ, como
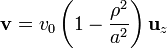
El líquido posee una densidad de carga uniforme ρ0, de forma que la densidad de corriente es 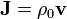 . En el exterior del tubo no hay corriente.
. En el exterior del tubo no hay corriente.
- Halle el campo magnético que se produce tanto en el interior de la tubería como en el exterior de ella.
- Calcule la fuerza que el campo magnético ejerce sobre una carga q que se mueve con el líquido, a una distancia a / 2 del eje.
22  Fuerza entre un hilo y un dipolo magnético
Fuerza entre un hilo y un dipolo magnético
Por un cable vertical muy largo, se hace circular una corriente I0. Un pequeño imán (equivalente a un dipolo magnético 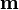 ), de peso
), de peso  , se suspende de un hilo ideal, de longitud l, cuyo punto de sujeción se encuentra a una distancia a del cable. El imán está sujeto por su punto central, de forma que puede orientarse libremente. ¿En que dirección apuntará el imán? Calcule la fuerza magnética sobre el imán, cuando se encuentra a una distancia x del cable. Halle la ecuación para el ángulo que el hilo forma con la vertical.
, se suspende de un hilo ideal, de longitud l, cuyo punto de sujeción se encuentra a una distancia a del cable. El imán está sujeto por su punto central, de forma que puede orientarse libremente. ¿En que dirección apuntará el imán? Calcule la fuerza magnética sobre el imán, cuando se encuentra a una distancia x del cable. Halle la ecuación para el ángulo que el hilo forma con la vertical.
23  Energía de interacción entre dos dipolos
Energía de interacción entre dos dipolos
Sobre una mesa horizontal se colocan dos brújulas (equivalentes a dipolos magnéticos) iguales, de forma que sus centros distan una cantidad a. Las dos brújulas pueden girar en el plano horizontal. Considerando que la interacción brújula-brújula es mucho mayor que la acción del campo magnético terrestre, ordene las cuatro configuraciones de la figura de menor a mayor energía. ¿Cómo se orientarán las brújulas?
24  Fuerza entre un dipolo y una espira
Fuerza entre un dipolo y una espira
Se tiene un pequeño imán, modelable como un dipolo magnético puntual de momento magnético 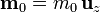 , situado a una cierta altura z sobre el eje de una espira circular de radio a por la que circula una corriente eléctrica continua de intensidad I0.
, situado a una cierta altura z sobre el eje de una espira circular de radio a por la que circula una corriente eléctrica continua de intensidad I0.
Calcule la fuerza que la espira ejerce sobre el dipolo, y la que el dipolo produce sobre la espira. ¿Se verifica la tercera ley de Newton?
25  Momento magnético de una esfera en rotación
Momento magnético de una esfera en rotación
Calcule el momento magnético dipolar de una esfera de radio R, con una carga q distribuida uniformemente en su volumen y que gira con velocidad angular  .
.
Establezca la proporcionalidad entre este momento magnético y el momento angular de la esfera, si ésta posee una masa m distribuida uniformemente en el volumen.







