Problemas de campo eléctrico (GIA)
De Laplace
1 Carga total en un cubo de cobre
Se tiene un cubo de cobre de 1 cm de arista. Calcula la cantidad de carga positiva y negativa que hay en el cubo. Si en un instante dado, los dos tipos de carga se separasen ocupando cada uno una mitad del tubo, estima la aceleración que sufriría cada una de las mitades si el cubo se dividiera en ese instante.
Datos: Número atómico del cobre Z = 29, 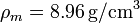 ,
, 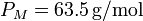 .
.
2 Densidades de carga eléctrica
Calcula la carga eléctrica total en cada uno de estos sistemas
- Uno hilo recto de longitud L con una densidad lineal de carga uniforme λ0.
- Un hilo recto de longitud L con densidad lineal de carga
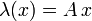 (x = 0 corresponde al punto medio).
(x = 0 corresponde al punto medio).
- Un hilo circular con densidad de carga lineal uniforme λ0.
- Un disco de radio R y grosor nulo con densidad superficial de carga uniforme σ0.
- Una esfera de radio R con densidad de carga volumétrica uniforme ρ0.
- Una esfera de radio R con densidad de carga volumétrica
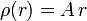 , siendo r la distancia al centro de la esfera.
, siendo r la distancia al centro de la esfera.
3 Electroscopio
Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud L. Cada esfera tiene una masa m y está sometida a la gravedad g. Las cargas pueden considerarse como puntuales e iguales entre sí. Halla la ecuación que liga el semiángulo θ con el valor de la carga total Q depositada en las esferas.
Supón que la masa de cada esfera es 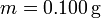 y la longitud del cable del que penden es
y la longitud del cable del que penden es 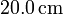 . Admite asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1o. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
. Admite asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1o. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?
4 Superposición de fuerzas electrostáticas en sistema de cargas puntuales
Dos partículas con cargas eléctricas q1 = q2 = 1μC se encuentran situadas en las posiciones 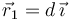 y
y 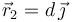 , siendo
, siendo 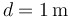 . Se coloca una tercera partícula con carga
. Se coloca una tercera partícula con carga 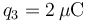 en
en 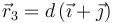 .
.
- Calcular la fuerza sobre q3.
- ¿Qué valor ha de tener una carga q4 situada en el origen para que la fuerza neta sobre la partícula con carga q3 pase a ser nula?
5 Fuerza eléctrica en sistema de cuatro cargas puntuales
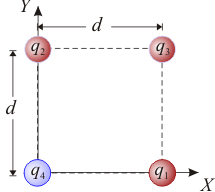
Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia OXYZ, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometríadel sistema es tal que la distancia que separa dos carta contiguas es
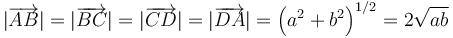
No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.
- ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula,
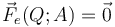 ?
?
- En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?
6 Campo eléctrico entre dos cargas puntuales
Se tienen dos cargas puntuales q1 y q2 separadas por una distancia d. Determina el punto sobre la línea que las une en el que el campo eléctrico se anula para cada uno de estos casos
-
 .
.
-
 .
.
-
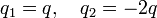 .
.
- q1 y q2 arbitrarios.
7 Campo eléctrico en el vértice de un cuadrado
En tres de los vértices de un cuadrado de lado 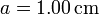 tenemos sendas cargas puntuales q1, q2 y q3. Calcula el campo eléctrico en el vértice sin carga en cada uno de los siguientes casos.
tenemos sendas cargas puntuales q1, q2 y q3. Calcula el campo eléctrico en el vértice sin carga en cada uno de los siguientes casos.
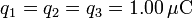 .
.
-
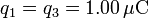 ,
, 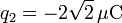 .
.
-
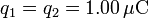 ,
, 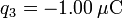 .
.
8 Campo eléctrico en el eje de un anillo, de una corona circular y de un disco
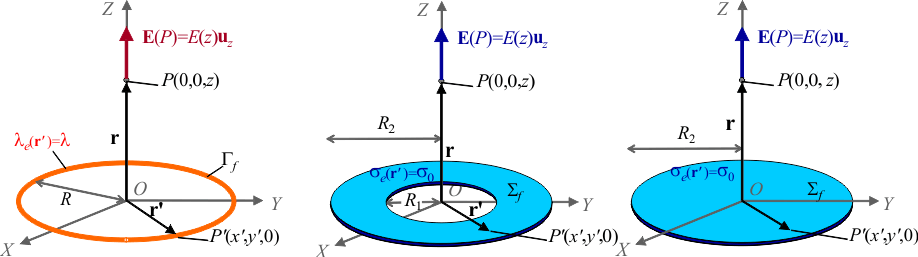
Halle el campo eléctrico en todos los puntos del eje de un anillo de radio R sobre el cual hay una densidad de carga uniforme λ.
A partir de este resultado, calcule el campo creado por una corona circular de radios R1 y R2 (R1 < R2), sobre la cual hay una densidad de carga uniforme σ0, en los puntos de su eje.
¿A qué se reduce si 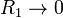 ? ¿Y si
? ¿Y si 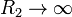 ? Considere en particular el comportamiento en las proximidades de z = 0.
? Considere en particular el comportamiento en las proximidades de z = 0.
9 Flujo de campo eléctrico de carga puntual y barra cargada
Se tiene una barra de ebonita de sección despreciable y longitud 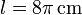 , que tras frotarla con lana adquiere una carga eléctrica negativa
, que tras frotarla con lana adquiere una carga eléctrica negativa 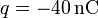 uniformemente distribuidos a lo largo de la barra. Además, existe una carga puntual positiva
uniformemente distribuidos a lo largo de la barra. Además, existe una carga puntual positiva 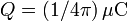 , situada a una distancia
, situada a una distancia 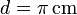 del centro O de la barra, en dirección perpendicular a ésta. Determínese el flujo del campo eléctrico a través de una superficie esférica de radio
del centro O de la barra, en dirección perpendicular a ésta. Determínese el flujo del campo eléctrico a través de una superficie esférica de radio 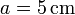 y centro en O.
y centro en O.
Datos: Valor de la constante electrostática (o de
Coulomb), 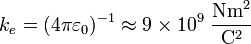
10 Campo eléctrico de esfera cargada uniformemente
Una carga Q se distribuye uniformemente en el volumen de una esfera de radio R. Calcule el campo eléctrico dentro y fuera de la esfera.
11 Campo eléctrico de esfera cargada en su superficie
Una carga Q se distribuye uniformemente en la superficie de una esfera de radio R. Calcule el campo eléctrico dentro y fuera de la esfera.
12 Campo eléctrico de distribución volumétrica de carga con simetría radial
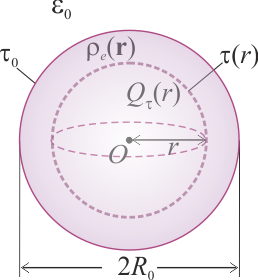
En una esfera τ0 de radio R0 y centro en O, existe una distribución no uniforme de carga eléctrica negativa descrita por una densidad volumétrica radial ρe(r), respecto del punto O, de manera que r es la distancia desde dicho centro al punto P donde se mide la densidad de carga. Dicha distribución es tal que si consideramos una región esférica τ con centro en O y radio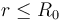 , la cantidad parcial de carga contenida en τ es
, la cantidad parcial de carga contenida en τ es 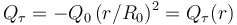 . No hay más cargas en el sistema.
. No hay más cargas en el sistema.
- ¿Cómo es la componente radial del campo eléctrico E(r) creado por la distribución descrita, tanto dentro como fuera de la esfera τ0?
- ¿Cómo es el potencial electrostático creado por la distribución en el exterior de τ0? ¿Cuánto vale el potencial en el centro O?
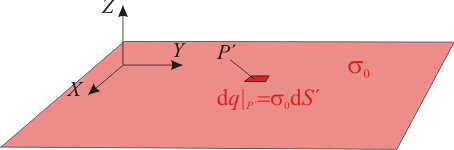
13 Campo eléctrico de un plano cargado
Sobre una superficie plana que puede considerarse infinita, se ha depositado una densidad superficial de carga uniforme, σ0.- Calcúlese el campo eléctrico a ambos lados del plano.
- Se dispone ahora otro plano, paralelo al anterior a una distancia d, y con una densidad superficial de carga uniforme − σ0. Halle el campo eléctrico en todos los puntos del espacio.
14 Corteza esférica conductora con hueco relleno de carga
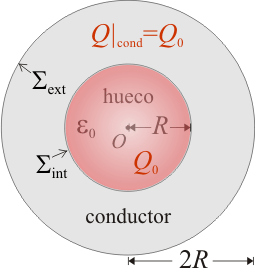
Se tiene una esfera metálica (conductor perfecto) de radio 2R, que tiene en su interior un hueco concéntrico de radio R. La corteza de material conductor comprendida entre las superficies interior (Σint) y exterior (Σext), de radio R y 2R, respectivamente, está perfectamente aislada y cargada eléctricamente con una cantidad fija Q0 de carga libre. El hueco está relleno de un gas cargado eléctricamente con una cantidad de carga Q0, que se considera uniformemente distribuida en todo el volumen del hueco. Asumiendo que el sistema se halla en equilibrio electrostático...- ¿Cómo se distribuye la carga Q0 en la corteza conductora?
- Obtenga la expresión del campo eléctrico en todo el espacio.
15 Carga puntual en un hueco conductor
Una carga puntual positiva de 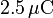 se sitúa en el centro de una corteza esférica de radio interior
se sitúa en el centro de una corteza esférica de radio interior 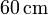 y radio exterior
y radio exterior 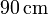 .
.
- Determina la expresión del campo eléctrico en todos los puntos del espacio.
- Determina las densidades superficiales de carga eléctrica en las superficies interior y exterior de la corteza, así como la carga total de esta.
- ¿Como se ve afectado la densidad de carga en la superficie exterior si la carga puntual no está en el centro de la cavidad?
- Repetir los apartados anteriores en caso de que se añada una carga neta de + 3.5μC a la corteza.
16 Campo eléctrico de un dipolo
Tenemos dos cargas puntuales de la misma magnitud y signo contrario separadas una distancia d.
- Encuentra la expresión que da el campo eléctrico en los puntos de la línea que une ambas cargas.
- Encuentra la expresión que da el campo eléctrico en los puntos de la línea perpendicular a la línea que une las dos carga y pasa por el punto equidistante entre ellas.
- En los dos casos anteriores, ¿cómo el es campo eléctrico cuando la distancia al punto medio es grande?
17 Fuerza sobre un dipolo
Se tiene un dipolo eléctrico 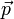 situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
18 Dipolo eléctrico en distribución esférica de carga
Un gas ionizado encerrado en una esfera puede modelarse como una distribución de carga con densidad volumétrica uniforme de valor ρ0. En su interior hay una molécula de agua, con carga total nula, pero que puede considerarse como un dipolo formado por dos cargas opuestas, ambas de valor absoluto 2e, separadas una distancia δ. Si inicialmente la molécula está situada en el punto central O de la distribución de carga, ¿qué ocurre después?
19 Campo eléctrico de esfera con distribución no uniforme de carga
Utilizando la ley de Gauss calcula el campo eléctrico creado por una esfera de radio R con densidad volumétrica de carga 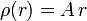 , siendo r la distancia al centro de la esfera.
, siendo r la distancia al centro de la esfera.