Fuerza sobre un dipolo GIA
De Laplace
1 Enunciado
Se tiene un dipolo eléctrico 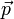 situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
situado a una distancia x de un hilo infinito cargado uniformemente con densidad de carga uniforme λ0. Admitiendo que el dipolo está orientado en la dirección del campo creado por el hilo, encuentra la expresión de la fuerza que el hilo crea sobre el dipolo.
2 Solución
El campo creado por un hilo infinito con una densidad lineal de carga uniforme λ0 es
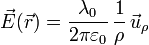
siendo ρ la distancia desde el punto al hilo y 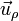 un vector unitario que se aleja del hilo en cada instante.
un vector unitario que se aleja del hilo en cada instante.
Elegimos los ejes de modo que el eje Z coincida con el hilo cargado y el eje X pase por el punto donde está el dipolo y su dirección coincida con su orientación. La posición del dipolo viene dada por el vector
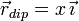
Y el campo en el eje X es
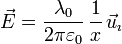
Con nuestra elección de ejes la distancia desde un punto del eje X al hilo es x, y el vector 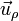 en los puntos del eje coincide con el vector
en los puntos del eje coincide con el vector 
Un dipolo está compuesto por dos cargas puntuales de igual magnitud y signo opuesto separadas por una distancia d pequeña. El enunciado nos dice que el dipolo está orientado en la dirección y sentido del campo. Por tanto, las posiciones de las cargas negativa y positiva que forman el dipolo son

La fuerza que el campo ejerce sobre el dipolo es la suma de la fuerza sobre cada una de las cargas que lo componen.

Sustituyendo los vectores de posición en la expresión del campo tenemos

Usamos la condición de que d es muy pequeña. Podemos escribir la fuerza como
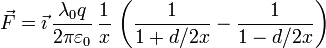
Utilizamos ahora el desarrollo de Taylor

En el primer paréntesis se tiene δ = 2d / x, y en el segundo δ = − 2d / x. En ambos casos n = − 1. La fuerza se puede aproximar por
![\vec{F} \simeq \vec{\imath}\,\dfrac{\lambda_0q}{2\pi\varepsilon_0}\,\dfrac{1}{x}\,
\left[ \left(1-\dfrac{d}{2x}\right) - \left(1+\dfrac{d}{2x}\right)\right]
=-\dfrac{\lambda_0qd}{2\pi\varepsilon_0}\,\dfrac{1}{x^2}\,\vec{\imath}](/wiki/images/math/0/0/a/00adaaf95a677ba70b92e13fe236c95b.png)
Por tanto, la fuerza puede aproximarse por
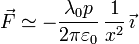
siendo p = qd el momento dipolar del dipolo. Suponiendo que λ0 es positiva, la fuerza es atractiva, lo cual tiene sentido pues la carga negativa está más cerca del hilo.
Aplicando el Principio de Acción y Reacción, la fuerza que el dipolo ejerce sobre el hilo es igual a esta con el signo cambiado.





