Entrar Página Discusión Historial Go to the site toolbox

Cálculo de campo eléctrico usando la ley de Gauss GIA

De Laplace

Contenido

1 Enunciado

Utilizando la ley de Gauss calcula el campo eléctrico creado por una esfera de radio R con densidad volumétrica de carga 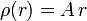\rho(r) = A\,r, siendo r la distancia al centro de la esfera.

2 Solución

2.1 Esfera con densidad volumétrica dependiente de r

En este problema se conserva la simetría esférica, por lo que el campo sigue teniendo la forma

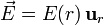
\vec{E} = E(r)\,\mathbf{u}_r

siendo r la distancia al centro de la esfera y 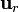\mathbf{u}_r un vector radial respecto al centro de la esfera de módulo unidad. Podemos usar la ley de Gauss para calcular el campo eléctrico

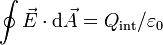
\oint\vec{E}\cdot\mathrm{d}\vec{A} = Q_{\mathrm{int}}/\varepsilon_0

Escogemos una esfera de radio r concéntrica con la esfera como superficie gaussiana. Dada la forma del campo, el flujo a través suyo para cualquier valor de r es

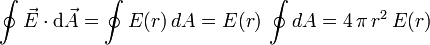
\oint\vec{E}\cdot\mathrm{d}\vec{A} = \oint E(r)\,dA = E(r)\,\oint dA = 4\,\pi\,r^2\,E(r)

La carga interior a la superficie gaussiana sí depende de su radio. Consideramos dos casos, que estemos en el exterior o el interior de la esfera.

2.1.1 Exterior de la esfera

Aquí tenemos r > R, La carga interior es la carga total de la esfera, independientemente del valor de r. Esta carga la hemos calculado en un problema anterior. Podemos considerar que la esfera está compuesta por un número infinito de cortezas esféricas concéntricas de radio r' y grosor dr'. El volumen de cada esfera es

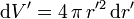
\mathrm{d}V' = 4\,\pi\,r'^2\,\mathrm{d}r'

y la carga de cada una es la densidad de carga multiplicada por este volumen

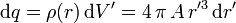
\mathrm{d}q = \rho(r)\,\mathrm{d}V' = 4\,\pi\,A\,r'^3\,\mathrm{d}r'

La carga total es la integral de esta expresión entre 0 y el radio de la esfera R

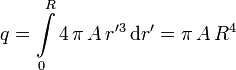
q = \int\limits_0^R 4\,\pi\,A\,r'^3\,\mathrm{d}r' = \pi\,A\,R^4

Esta la carga interior a la superficie gaussiana, por lo que el campo en el exterior de la esfera es

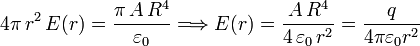
4\pi\,r^2\,E(r) = \dfrac{\pi\,A\,R^4}{\varepsilon_0} \Longrightarrow E(r) = \dfrac{A\,R^4}{4\,\varepsilon_0\,r^2} = \dfrac{q}{4\pi\varepsilon_0r^2}

En el exterior de la esfera el campo es el mismo que el que crearía una carga puntual situada en su centro y de magnitud igual a la carga total de la esfera.

2.1.2 Interior de la esfera

En este caso la carga en el interior de la superficie gaussiana sí depende de su radio, pues sólo una parte de la esfera queda dentro. La carga dentro de la superficie gaussiana es

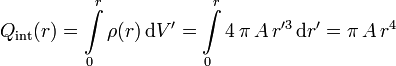
Q_{\mathrm{int}}(r) = \int\limits_0^r \rho(r)\,\mathrm{d}V' = \int\limits_0^r 4\,\pi\,A\,r'^3\,\mathrm{d}r' = \pi\,A\,r^4

A partir del flujo obtenemos el valor del campo eléctrico en esta región

4\pi\,r^2\,E(r) = \dfrac{\pi\,A\,r^4}{\varepsilon_0} \Longrightarrow E(r) = \dfrac{A\,r^2}{4\,\varepsilon_0}

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_campo_el%C3%A9ctrico_usando_la_ley_de_Gauss_GIA"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:33, 1 mar 2012. - Esta página ha sido visitada 18.858 veces. - Aviso legal - Acerca de Laplace