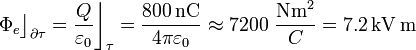Flujo del campo eléctrico de carga puntual y barra cargada (F2GIA)

De Laplace

1 Enunciado

Se tiene una barra de ebonita de sección despreciable y longitud 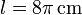$l=8\pi\,\mathrm{cm}\,$ , que tras frotarla con lana adquiere una carga eléctrica negativa 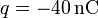$q=-40\,\mathrm{nC}\,$ uniformemente distribuidos a lo largo de la barra. Además, existe una carga puntual positiva 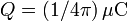$Q=(1/4\pi)\,\mu\mathrm{C}\,$ , situada a una distancia 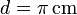$d=\pi\,\mathrm{cm}$ del centro $O$ de la barra, en dirección perpendicular a ésta. Determínese el flujo del campo eléctrico a través de una superficie esférica de radio 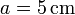$a=5\,\mathrm{cm}$ y centro en $O$ .

Datos: Valor de la constante electrostática (o de Coulomb), 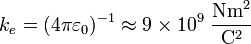$\displaystyle \quad k_e=(4\pi\varepsilon_0)^{-1}\approx 9\times 10^9\ \frac{\mathrm{Nm}^2}{\mathrm{C}^2}$

2 Solución

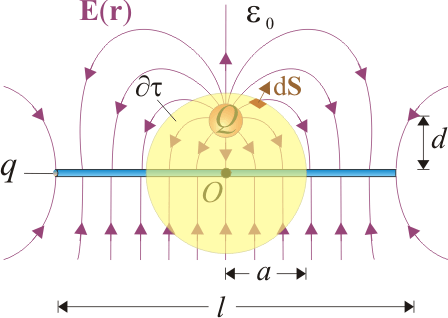
La carga eléctrica puntual

Q

y la distribuida en la barra,

q

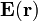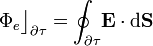
, son fuentes del campo eléctrico $\mathbf{E} (\mathbf{r})$ , cuyo flujo a través de la superficie esférica $\partial \tau$ se define como, $\Phi_e\big\rfloor_{\partial \tau}=\oint_{\partial\tau}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}$

En principio, el primer paso sería obtener el campo eléctrico creado por la distribución de carga descrita y, posteriormente, calcular la anterior integral de superficie. Pero, dadas las geometrías de la distribución de cargas y de la superficie cerrada, este procedimiento resulta bastante complicado. Pero podemos seguir un método bastante más rápido y sencillo: según la ley de Gauss, el flujo del campo eléctrico será proporcional a la cantidad de carga eléctrica encerrada dentro de dicha superficie:

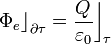
$\Phi_e\big\rfloor_{\partial \tau}=\frac{Q}{\varepsilon_0}\bigg\rfloor_{\tau}$

Luego sólo nos qeda determinar la cantidad total de carga eléctrica que se halla en el interior del volumen delimitado por la superficie esférica de radio $a$ y centrada en el punto medio $O$ de la barra cargada. Como,

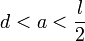
$d<a<\frac{l}{2}$

la carga puntual $Q$ se encuentra en el interior de la superficie gaussiana $\partial\tau$ . Pero sólo el fragmento de barra cargada que coincide con un diámetro, contribuirá al valor del flujo.

Esta cantidad de carga correspondiente a la barra se obtiene a partir de su densidad lineal de carga eléctrica. Y como ésta se distribuye uniformemente, la densidad será igual a la cantidad total de carga dividida por la longitud:

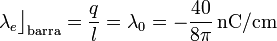
$\lambda_e\big\rfloor_\mathrm{barra}=\frac{q}{l}=\lambda_0=-\frac{40}{8\pi}\,\mathrm{nC/cm}\,$

Por tanto, se tendrá:

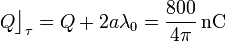
$Q\big\rfloor_{\tau}=Q+2 a\lambda_0=\frac{800}{4\pi}\,\mathrm{nC}\,$

Sustituyendo estos valores en la expresión del flujo, se obtiene:

$\Phi_e\big\rfloor_{\partial \tau}=\frac{Q}{\varepsilon_0}\bigg\rfloor_{\tau}=\frac{800\,\mathrm{nC}}{4\pi\varepsilon_0}\approx 7200\ \frac{\mathrm{Nm}^2}{C}=7.2\,\mathrm{kV}\,\mathrm{m}$

Flujo del campo eléctrico de carga puntual y barra cargada (F2GIA)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES