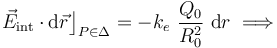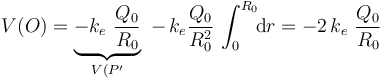Campo eléctrico de distribución volumétrica de carga con simetría radial(GIA)
De Laplace
Contenido |
1 Enunciado
En una esfera τ0 de radio R0 y centro en O, existe una distribución no uniforme de carga eléctrica negativa descrita por una densidad volumétrica radial ρe(r), respecto del punto O, de manera que r es la distancia desde dicho centro al punto P donde se mide la densidad de carga. Dicha distribución es tal que si consideramos una región esférica τ con centro en O y radio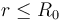 , la cantidad parcial de carga contenida en τ es
, la cantidad parcial de carga contenida en τ es 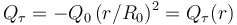 . No hay más cargas en el sistema.
. No hay más cargas en el sistema.
- ¿Cómo es la componente radial del campo eléctrico E(r) creado por la distribución descrita, tanto dentro como fuera de la esfera τ0?
- ¿Cómo es el potencial electrostático creado por la distribución en el exterior de τ0? ¿Cuánto vale el potencial en el centro O?
2 Solución
- Planteamiento
Tomando un sistema de referencia con OXYZ con origen en el centro O de la region esférica τ0, la distribución de carga eléctrica existente en el sistema estará descrita por una función densidad volumétrica que indica la cantidad de carga que por unidad de volumen hay en cada punto del espacio. Si para cada punto P del espacio definimos el radiovector 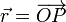 que determina la posición de dicho punto respecto del centro O, se tendrá:
que determina la posición de dicho punto respecto del centro O, se tendrá:
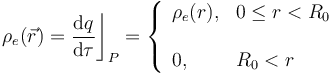
con  . La función
. La función 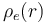 no está especificada, pero podría calcularse a partir del dato proporcionado en el enunciado de que la cantidad parcial de carga eléctrica que hay en una esfera τ contenida en τ0, con centro en O y radio
no está especificada, pero podría calcularse a partir del dato proporcionado en el enunciado de que la cantidad parcial de carga eléctrica que hay en una esfera τ contenida en τ0, con centro en O y radio 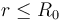 , está descrita por la expresión:
, está descrita por la expresión:
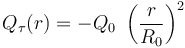
En consecuencia, la cantidad total de carga en τ0 es 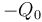 . En cualquier caso, aún desconociendo a priori la expresión de la función
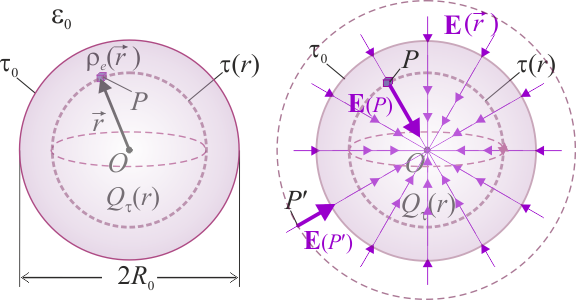
. En cualquier caso, aún desconociendo a priori la expresión de la función 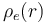 , el hecho de que sea sólo dependa de la distancia r al centro O (distribución radial), nos permite asegurar que el campo eléctrico creado por dicha distribución en cualquier punto P del espacio va a presentar simetría radial con respecto a dicho punto. Es decir,
, el hecho de que sea sólo dependa de la distancia r al centro O (distribución radial), nos permite asegurar que el campo eléctrico creado por dicha distribución en cualquier punto P del espacio va a presentar simetría radial con respecto a dicho punto. Es decir,
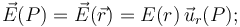
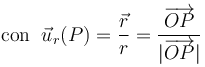
Es decir, el campo eléctrico en un punto cualquiera del espacio, P, sólo tiene componente radial (en la dirección del radiovector 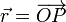 ), que depende de la distancia r al centro O de la distribución, pero no de otras variables geométricas. Y en el caso de campos que presentan este tipo de simetría, la expresión de dicha componente radial,
), que depende de la distancia r al centro O de la distribución, pero no de otras variables geométricas. Y en el caso de campos que presentan este tipo de simetría, la expresión de dicha componente radial, 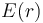 , puede obtenerse mediante la aplicación de la Ley de Gauss para el campo eléctrico.
, puede obtenerse mediante la aplicación de la Ley de Gauss para el campo eléctrico.
Esta ley fundamental de la Teoría Electromagnética establece que el flujo del campo eléctrico a través de una superficie cerrada 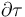 , es proporcional a la cantidad total de carga eléctrica que hay en el volumen τ delimitado por aquélla. El valor de la constante de proporcionalidad depende del sistema de unidades utilizado para medir las magnitudes físicas; en el Sistema Internacional de unidades esta constante es
, es proporcional a la cantidad total de carga eléctrica que hay en el volumen τ delimitado por aquélla. El valor de la constante de proporcionalidad depende del sistema de unidades utilizado para medir las magnitudes físicas; en el Sistema Internacional de unidades esta constante es 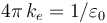 , (inverso de la permitividad dieléctrica del vacío):
, (inverso de la permitividad dieléctrica del vacío):
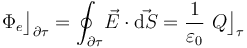
Por otra parte, la Ley de Gauss para el campo eléctrico expresa una relación cuantitativa entre dicha magnitud vectorial y sus fuentes escalares: es decir, las magnitudes escalares que producen campo eléctrico.
2.1 Cálculo de la componente radial del campo eléctrico
Para determinar la componenente del campo con simetría radial mediante la ley de Gauss, ésta ha de aplicarse en una superficie cerrada con idéntica simetría. En el caso que nos ocupa hemos de considerar una superfice esférica  con centro en O. Es decir, concéntrica con la distribución de carga que genera el campo y, por tanto, con el propio campo.
con centro en O. Es decir, concéntrica con la distribución de carga que genera el campo y, por tanto, con el propio campo.
El flujo de un campo vectorial a través de una superficie se obtiene calculando la integral, extendida a toda la superficie, del producto del campo en cada punto P de  , multiplicado escalarmente por el vector elemento de superficie
, multiplicado escalarmente por el vector elemento de superficie 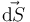 en dicho punto. Como se sabe, este vector tiene módulo infinitesimal
en dicho punto. Como se sabe, este vector tiene módulo infinitesimal 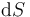 (área del entorno del punto), dirección perpendicular al plano tangente a la superficie en P y, por convenio, orientado hacia el exterior del volumen delimitado por la superficie
(área del entorno del punto), dirección perpendicular al plano tangente a la superficie en P y, por convenio, orientado hacia el exterior del volumen delimitado por la superficie 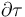 . Y puesto que en una superfice esférica de centro O, el radio OP es perpendicular al plano tangente en P a la superficie
. Y puesto que en una superfice esférica de centro O, el radio OP es perpendicular al plano tangente en P a la superficie 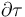 , se tendrá que
, se tendrá que
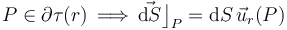
donde 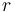 es el radio de la superficie esférica
es el radio de la superficie esférica 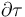 y, por tanto, la distancia desde el centro O a todos y cada uno de los puntos de dicha superficie.
y, por tanto, la distancia desde el centro O a todos y cada uno de los puntos de dicha superficie.
El vector unitario radial 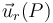 es exactamente el mismo tanto en la expresión del vector elemento de superficie como del campo (por estar evaluados ambos en el mismo punto P de la superficie).Por otra parte, puesto que la componente radial E(r) sólo depende la distancia al centro O, dicha componente tendrá igual valor en todos los puntos de
es exactamente el mismo tanto en la expresión del vector elemento de superficie como del campo (por estar evaluados ambos en el mismo punto P de la superficie).Por otra parte, puesto que la componente radial E(r) sólo depende la distancia al centro O, dicha componente tendrá igual valor en todos los puntos de 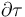 . Por tanto, se obtiene...
. Por tanto, se obtiene...
![\forall\, P\in\partial\tau(r)\,\mathrm{,}\,\;\;\vec{E}\cdot\vec{\mathrm{d}S}\big\rfloor_{P}=\big[E(r)\!\ \vec{u}_r(P)\big]\cdot\big[\mathrm{d}S\!\ \vec{u}_r(P)]=E(r)\!\ \mathrm{d}S\;\;\Longrightarrow\;\; \Phi_e\big\rfloor_{\partial\tau}=\oint_{\partial\tau}\!\! \vec{E}\cdot\vec{\mathrm{d}S}=E(r)\!\ \oint_{\partial\tau}\!\!\mathrm{d}S=E(r)\ 4\pi\!\ r^2](/wiki/images/math/1/5/6/156f60fc1b5bcf39f2f473535572948f.png)
Este resultado es válido independientemente de que 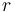 sea mayor o menor que
sea mayor o menor que 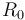 (radio de la distribución de carga). Sin embargo, la cantidad de carga contenida dentro de la superficie esférica
(radio de la distribución de carga). Sin embargo, la cantidad de carga contenida dentro de la superficie esférica 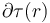 , sí va a depender del valor del radio de esta. Si el radio es menor que el de la distribución de carga eléctrica, la cantida de carga contenida es proporcional al cuadrado del radio, tal como se incida en el enunciado. Si el radio de la supeficie gaussiana cerrada
, sí va a depender del valor del radio de esta. Si el radio es menor que el de la distribución de carga eléctrica, la cantida de carga contenida es proporcional al cuadrado del radio, tal como se incida en el enunciado. Si el radio de la supeficie gaussiana cerrada 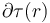 es mayor o igual que el de τ0, la cantidad de carga contenida será
es mayor o igual que el de τ0, la cantidad de carga contenida será 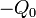 :
:
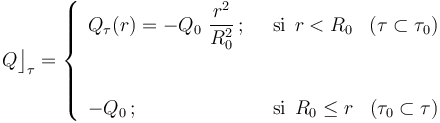
Aplicando ahora la ley de Gauss, se obtiene...
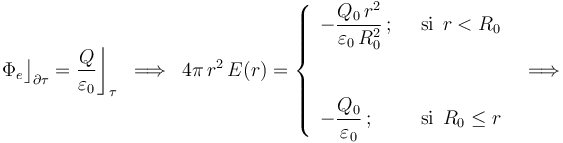
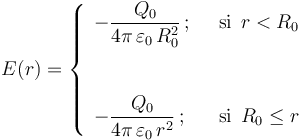
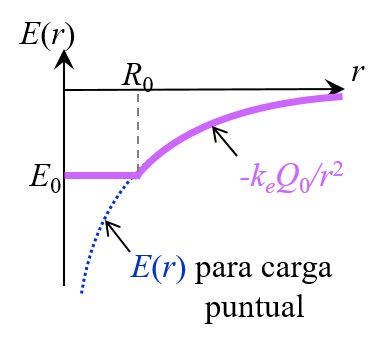
Por tanto, la distribución de carga en τ0 genera un campo eléctrico radial en todo el espacio, expresado por la siguiente función de campo:
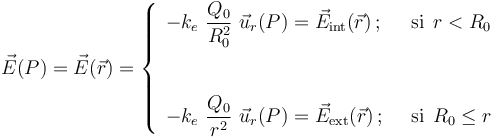
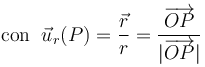
Es decir, en los puntos interiores a la distribución la intensidad del campo es constante; mientras que en los puntos exteriores el campo es idéntico al de una carga puntual  localizada en el centro O de τ0.
localizada en el centro O de τ0.
2.2 Potencial electrostático
Este resultado nos permite identificar de forma inmediata cómo va a ser el campo potencial electrostático 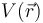 en puntos exteriores a la distribución. Puesto que dicho potencial está relacionado directamente con el campo eléctrico por las relaciones,
en puntos exteriores a la distribución. Puesto que dicho potencial está relacionado directamente con el campo eléctrico por las relaciones,
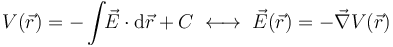
si el campo eléctrico en puntos exteriores a τ0 es el mismo al de una carga puntual situada en O, en esa región el potencial electrostático debe ser también el correspondiente a dicha distribución simple de carga... salvo una constante C cuyo valor puede fijarse arbitrariamente:
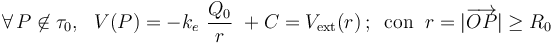
El dominio de definición de esta función se extiende hasta puntos infitamente alejados de la distribución de carga. Asumiendo ésta no va producir efectos apreciables en dichos puntos y que, por tanto, el potencial se anula allí, se tendrá que...
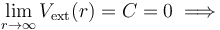
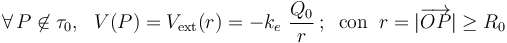
- Valor del potencial en el centro de la distribución
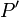 de la superficie
de la superficie 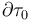 de la esfera cargada:
de la esfera cargada:

Entonces, el valor del potencial en el centro O puede ser calculado sin más que aplicar la definición de diferencia de potencial entre dos puntos:
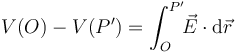
Como se sabe, si el campo eléctrico es producido exclusivamente por cargas electrostáticas, el valor de la circulación del campo eléctrico que aparece en la expresión anterior es idependiente del camino seguido. Elijamos, por tanto, un camino que nos permita el cálculo sencillo de dicha integral: el radio Δ que va desde el centro O al punto 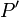 de la superficie
de la superficie 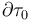 . En ese caso, el campo eléctrico ha de ser evaluado siempre en puntos interiores de τ0, donde comprobamos que existía un campo radial pero de igual módulo en todos ellos,
. En ese caso, el campo eléctrico ha de ser evaluado siempre en puntos interiores de τ0, donde comprobamos que existía un campo radial pero de igual módulo en todos ellos, 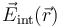 .
Además, a lo largo de esta trayectoria, el vector diferencial de camino
.
Además, a lo largo de esta trayectoria, el vector diferencial de camino 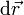 sólo tiene componente radial (es decir, es paralelo al campo eléctrico en cada punto de la misma), y su modulo va a ser una variación infinitesimal de la distancia al centro O:
sólo tiene componente radial (es decir, es paralelo al campo eléctrico en cada punto de la misma), y su modulo va a ser una variación infinitesimal de la distancia al centro O:
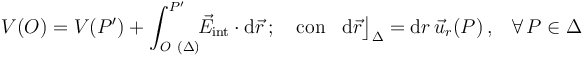
En consecuencia...