Dipolo eléctrico en distribución esférica de carga (F2GIA)

De Laplace

1 Enunciado

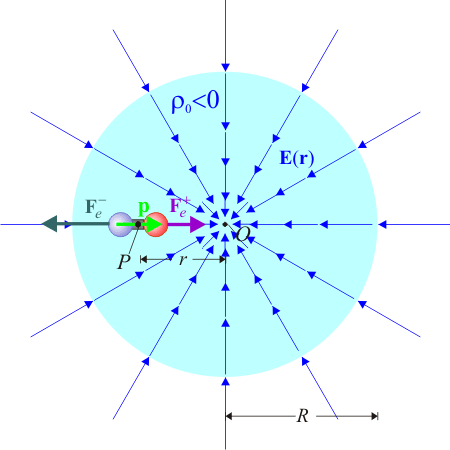
Un gas ionizado encerrado en una esfera puede modelarse como una distribución de carga con densidad volumétrica uniforme de valor $ρ 0$ . En su interior hay una molécula de agua, con carga total nula, pero que puede considerarse como un dipolo formado por dos cargas opuestas, ambas de valor absoluto $2 e$ , separadas una distancia $δ$ . Si inicialmente la molécula está situada en el punto central $O$ de la distribución de carga, ¿qué ocurre después?

2 Solución

En el interior de una esfera con carga eléctrica uniformemente distribuida en su volumen, el campo eléctrico tiene simetría radial, y su magnitud o intensidad en un punto es proporcional a la distancia $r$ desde dicho punto al centro de la distribución $O$ . Si la densidad volumétrica de carga es $ρ 0$ , el campo en un punto $P$ arbitrario del interior de la distribución es,

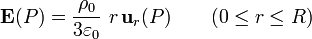
$\mathbf{E}(P)=\frac{\rho_0}{3\varepsilon_0}\ r\!\ \mathbf{u}_r(P)\qquad (0\leq r\leq R)$

y siendo 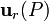$\mathbf{u}_r(P)$ el vector unitario en la dirección y sentido del segmento orientado $\overrightarrow{OP}$ .

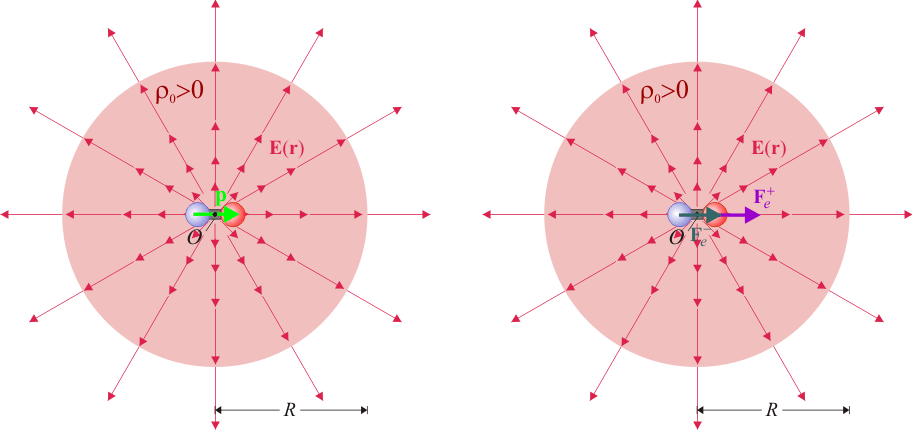
El dipolo eléctrico está caracterizado por su momento dipolar. Es esta una magnitud vectorial cuya dirección y sentido está determinada por el segmento orientado que, en el caso bajo estudio, va desde la posición de la carga $- 2 e$ a la de la carga positiva $+ 2 e$ . Cuando decimos que el dipolo se encuentra situado en el centro $O$ de la distribución de carga, es que allí está el punto medio del sistema formado por la dos cargas. En esta situación, ambas cargas se encuentran simétricamente dispuestas respecto de $O$ , en puntos de un mismo diámetro, por lo que posición de las cargas vendrá dada por los vectores:

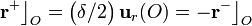
$\mathbf{r}^+\big\rfloor_O=\big(\delta/2\big)\!\ \mathbf{u}_r(O)=-\mathbf{r}^-\big\rfloor_O$

... donde 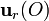$\mathbf{u}_r(O)$ indica la dirección arbitraria del dipolo cuando se coloca en el punto $O$ . Su momento dipolar en dicha posición será:

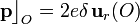
$\mathbf{p}\big\rfloor_O=2e\delta\!\ \mathbf{u}_r(O)$

Y en esta posición, el campo eléctrico no ejerce momento o par de fuerzas alguno,pues el campo eléctrico creado por la distribución uniforme de carga en el punto $O$ es nulo:

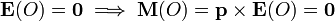
$\mathbf{E}(O)=\mathbf{0}\;\Longrightarrow\;\mathbf{M}(O)=\mathbf{p}\times\mathbf{E}(O)=\mathbf{0}$

Por tanto, si la molécula de agua se deja en reposo en el punto $O$ , no va a realizar movimiento de rotación alguno. Sin embargo, para determinar si permanece en dicho punto en estado de reposo absoluto, hemos de determinar si la molécula/dipolo está sometida a una fuerza resultante nula.

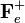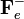Cada una de las dos cargas que componen el dipolo tiene carácter puntual, por tanto, al encontrarse en el seno de un campo eléctrico, se ejercerán sobre ellas sendas fuerzas $\mathbf{F}_e^+$ y $\mathbf{F}_e^-$ , que serán iguales al producto de la correspondiente carga por el valor del campo eléctrico en la posición que ocupa. La fuerza total ejercida sobre el dipolo será la suma de estas dos fuerzas. Cuando la partícula se halla en el punto $O$ , se tendrá:

$\left.\begin{array}{l}\displaystyle \mathbf{F}_e^+\big\rfloor_{O}=2e\!\ \mathbf{E}(O^+)\\ \\ \displaystyle\mathbf{F}_e^-\big\rfloor_{O}=-2e\!\ \mathbf{E}(O^-)\end{array}\right\} \;\;\Longrightarrow\quad\mathbf{F}_e\big\rfloor_{O}=\left[\mathbf{F}_e^++\mathbf{F}_e^-\right]_O=2e\!\ \big[\mathbf{E}(O^+)-\mathbf{E}(O^-)\big]$

Obsérvese que cuando el dipolo encuentra en el punto $O$ , las cargas $+ 2 e$ y $- 2 e$ se encentran ambas a una distancia $r = δ / 2$ del centro de la distribución. Así, aunque $δ$ va a ser un número muy pequeño (del orden de 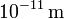$10^{-11}\,\mathrm{m}$ en el caso de la molécula de agua) es distinto de cero y, en consecuencia, ambas cargas están sometidas a la acción de un (débil) campo eléctrico. Pero obsérvese que en los puntos simétricos $O +$ y $O -$ , el campo eléctrico tendrá igual módulo y dirección, pero sentidos contrarios, por lo que el dipolo se verá sometido a una fuerza neta no nula:

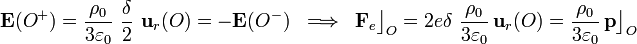
$\mathbf{E}(O^+)=\frac{\rho_0}{3\varepsilon_0}\ \frac{\delta}{2}\ \mathbf{u}_r(O)=-\mathbf{E}(O^-)\;\;\Longrightarrow\;\;\mathbf{F}_e\big\rfloor_{O}=2e\delta\ \frac{\rho_0}{3\varepsilon_0}\!\ \mathbf{u}_r(O)=\frac{\rho_0}{3\varepsilon_0}\!\ \mathbf{p}\big\rfloor_O$

Por tanto, si la carga distribuida uniformemente es positiva ( $ρ 0 > 0$ ), la molécula/dipolo (inicialmente en reposo) comenzará a desplazarse a lolargo del radio determinado por la dirección de 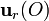$\mathbf{u}_r(O)$ , y con el sentido de su momento dipolar.

Supongamos que, al cabo de un cierto tiempo, la molécula/dipolo alcanza la posición

P

, a una distancia

r

del centro de la distribución. Aquí, el campo eléctrico es estrictamente no nulo, por lo que la molécula estará sometida a un par de fuerzas hasta que se cumpla:

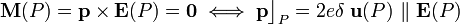
$\mathbf{M}(P)=\mathbf{p}\times\mathbf{E}(P)=\mathbf{0}\;\Longleftrightarrow\;\mathbf{p}\big\rfloor_P=2e\delta\ \mathbf{u}(P)\ \|\ \mathbf{E}(P)$

Es decir, si el dipolo se mueve libremente bajo la acción del campo eléctrico, se habrá desplazado desde $O$ hasta $P$ siempre alineado con la dirección del radio sobre el que se mueve. Consecuentemente, para toda posición $P$ se tendrá que 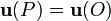$\mathbf{u}(P)=\mathbf{u}(O)$ . Es decir, el dipolo mantiene siempre su orientación inicial.

En cuanto a la fuerza resultante ejercida por el campo sobre la molécula en este punto...

$\mathbf{F}_e\big\rfloor_{P}=\left[\mathbf{F}_e^++\mathbf{F}_e^-\right]_P=2e\!\ \big[\mathbf{E}(P^+)-\mathbf{E}(P^-)\big]$

Ahora, el campo eléctrico en las posiciones ocupadas por las cargas $+ 2 e$ y $- 2 e$ tiene el mismo sentido, pero diferente intensidad (módulo), de manera que...

$\left.\begin{array}{l}\displaystyle\mathbf{E}(P^+)=\frac{\rho_0}{3\varepsilon_0}\ \left(r+\frac{\delta}{2}\right)\ \mathbf{u}_r(P)\\ \\ \displaystyle\mathbf{E}(P^-)=\frac{\rho_0}{3\varepsilon_0}\ \left(r-\frac{\delta}{2}\right)\ \mathbf{u}_r(P)\end{array}\right\} \;\;\Longrightarrow\;\;\mathbf{F}_e\big\rfloor_{P}=2e\delta\ \frac{\rho_0}{3\varepsilon_0}\!\ \mathbf{u}_r(P)=\frac{\rho_0}{3\varepsilon_0}\!\ \mathbf{p}\big\rfloor_P$

Como se vio anteriormente, el momento dipolar de la molécula está va a estar siempre orientado en la misma dirección (la inicial). Por tanto, si la carga distribuida es positiva, sobre la molécula actúa una fuerza constante en la dirección radial, que hace que el dipolo se mueva hacia la superficie de la esfera con su vector momento dipolar orientado en el sentido del movimiento. Obsérvese que, una vez que la molécula ha abandonado la posición inicial $O$ , las fuerzas sobre las cargas positiva y negativa del dipolo tienen sentidos opuestos, pero siempre va a ser mayor el módulo de la fuerza 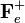$\mathbf{F}_e^+$ , pues la carga positiva se va a encontrar más alejada de $O$ que la negativa. 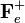En consecuencia, el sentido de la fuerza resultante es el mismo que el $\mathbf{F}_e^+$ .

Si la carga de la distribución es negativa ( $ρ 0 < 0$ ), el campo eléctrico en el interior de la esfera cambia su sentido, pero no su simetría radial ni la relación lineal de su módulo con la distancia al centro de la distribución. En consecuencia, cuando el dipolo se coloca en $O$ con una determinada orientación, experimenta una fuerza neta,

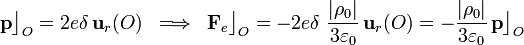
$\mathbf{p}\big\rfloor_O=2e\delta\!\ \mathbf{u}_r(O)\;\;\Longrightarrow\;\;\mathbf{F}_e\big\rfloor_{O}=-2e\delta\ \frac{|\rho_0|}{3\varepsilon_0}\!\ \mathbf{u}_r(O)=- \frac{|\rho_0|}{3\varepsilon_0}\!\ \mathbf{p}\big\rfloor_O$

que provocará el movimiento del dipolo en sentido contrario a la orientación de su momento dipolar. Como en el caso de la distribución positiva, cuando la molécula abandona la posición

O

la fuerza resultante se va a mantener constante, arrastrando otra vez a la molécula hacia la superficie de la esfera a lo largo de un radio, con el momento dipolar orientado en sentido contrario al del movimiento. Obsérvese que ahora la carga negativa es la que se va a encontrar más alejada del punto

O

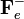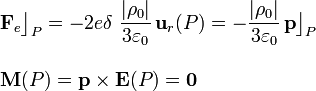
; por tanto, el sentido de la fuerza neta es el de la $\mathbf{F}_e^-$ , que ahora estará dirigido hacia el exterior de la distribución: $\begin{array}{l}\displaystyle \mathbf{F}_e\big\rfloor_{P}=-2e\delta\ \frac{|\rho_0|}{3\varepsilon_0}\!\ \mathbf{u}_r(P)=-\frac{|\rho_0|}{3\varepsilon_0}\!\ \mathbf{p}\big\rfloor_P\\ \\ \displaystyle \mathbf{M}(P)=\mathbf{p}\times\mathbf{E}(P)=\mathbf{0}\end{array}$

Por otra parte, de nuevo el momento dipolar estará orientado en la dirección y sentido del campo eléctrico (hacia el centro de la distribución), de manera que el momento resultante sigue siendo nulo. Cualquier variación de la orientación del dipolo provocaría la aparición de un momento que volvería a alinear a la molécula con el campo eléctrico.

Dipolo eléctrico en distribución esférica de carga (F2GIA)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES