De Laplace

Contenido

1 Problemas de boletín
2 Problemas adicionales
3 Preguntas de test

1 Problemas de boletín

1.1 Cálculos de carga total, campo y potencial

Calcule la carga total de las siguientes distribuciones de carga:

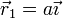$N$ cargas de valor $q$ situadas en los vértices de un polígono regular de $N$ lados situado en el plano $X Y$ , con centro el origen y cuyo primer vértice se encuentra en $\vec{r}_1=a\vec{\imath}$ .
Un anillo circular de radio $R$ con una densidad lineal de carga uniforme $λ 0$ .
Un anillo circular de radio $R$ con centro el origen y situado en el plano $X Y$ , con una densidad lineal de carga 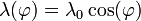$\lambda(\varphi)=\lambda_0\cos(\varphi)$ , siendo $\varphi$ el ángulo del vector de posición con el eje $O X$ .
Una superficie esférica de radio $a$ con una densidad de carga uniforme $σ 0$ , rodeada por una superficie esférica concéntrica de radio $b$ con densidad de carga $- σ 0$ .
Una esfera maciza de radio $R$ con densidad de carga uniforme $ρ 0$ .
Una esfera maciza de radio $R$ con una densidad de carga dependiente de la distancia al centro como

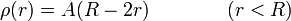
$\rho(r) = A(R-2r)\qquad\qquad (r < R)$

Calcule el campo y el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema

1.2 Campo de dos cargas

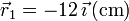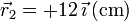Se tienen dos cargas $q 1$ y $q 2$ situadas respectivamente en los puntos $\vec{r}_1=-12\,\vec{\imath}\,(\mathrm{cm})$ y $\vec{r}_2=+12\,\vec{\imath}\,(\mathrm{cm})$ . Halle el campo eléctrico en los puntos

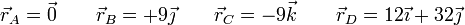
$\vec{r}_A=\vec{0}\qquad \vec{r}_B=+9\vec{\jmath}\qquad \vec{r}_C=-9\vec{k}\qquad \vec{r}_D=12\vec{\imath}+32\vec{\jmath}$

(todas las distancias en cm) para los cuatro casos siguientes

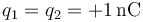
$q_1=q_2 = +1\,\mathrm{nC}$
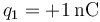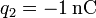
$q_1= +1\,\mathrm{nC}$ , $q_2=-1\,\mathrm{nC}$
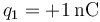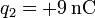
$q_1= +1\,\mathrm{nC}$ , $q_2=+9\,\mathrm{nC}$
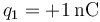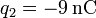
$q_1= +1\,\mathrm{nC}$ , $q_2=-9\,\mathrm{nC}$

Para los cuatro pares de cargas, localice el punto del eje OX en que se anula el campo eléctrico.

Calcule el potencial eléctrico para todos los casos en todos los puntos indicados.

1.3 Campo de distribuciones con simetría esférica

Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica:

Una superficie esférica de radio $a$ que almacena una carga $Q$ distribuida uniformemente.
Dos superficies esféricas concéntricas, de radios $a$ y $b$ ( $a < b$ ) que almacenan respectivamente cargas $+ Q$ y $- Q$ , distribuidas uniformemente.
Dos superficies esféricas concéntricas, de radios $a$ y $b$ ( $a <$ b) cargadas respectivamente con densidades superficiales uniformes $+ σ 0$ y $- σ 0$ .
Una esfera maciza de radio $R$ que almacena una carga $Q$ distribuida uniformemente en su volumen.
Una esfera maciza de radio $R$ con una densidad de carga dependiente de la distancia al centro como

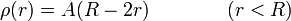
$\rho(r) = A(R-2r)\qquad\qquad (r < R)$

1.4 Dos esferas huecas

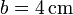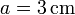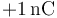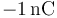
Se tiene un sistema de cargas formado por dos superficies esféricas de radio $b=4\,\mathrm{cm}$ cuyos centros distan $a=3\,\mathrm{cm}$ , como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de $+1\,\mathrm{nC}$ y $-1\,\mathrm{nC}$

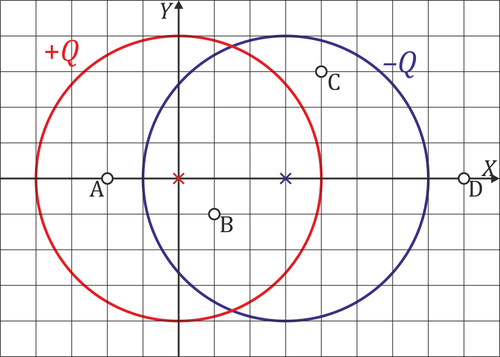
Para los puntos marcados en la figura (en cm)

$\vec{r}_A=-2\vec{\imath} \qquad \vec{r}_B=\vec{\imath}-\vec{\jmath} \qquad \vec{r}_C=4\vec{\imath}+3\vec{\jmath} \qquad \vec{r}_D=8\vec{\imath}$

Calcule el campo eléctrico.
Calcule el potencial eléctrico.
A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de 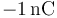$-1\,\mathrm{nC}$ desde el punto A al punto D moviéndola a lo largo del eje X.

1.5 Campo y potencial de una esfera con hueco

Se tiene una carga 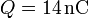$Q=14\,\mathrm{nC}$ distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 cm de la esfera grande.

Demuestre que el campo en el interior de la cavidad es uniforme y halle su valor.
Calcule el valor del campo en el exterior de la esfera en un punto situado sobre la recta que une los dos centros, a una distancia de 25 cm del centro de la esfera grande.
Calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.

1.6 Campo eléctrico de un anillo y un disco

Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio $R$ que almacena una carga $Q$ distribuida uniformemente.

A partir del resultado anterior calcule el campo en los puntos del eje de un disco circular de radio $R$ , en el cual existe una carga $Q$ distribuida uniformemente.

1.7 Campo eléctrico de un plano y de dos planos

Empleando el resultado del disco, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga $σ 0$ .

Suponga que se tienen dos planos infinitos paralelos separados una distancia a que almacenan respectivamente densidades de carga $+ σ 0$ y $- σ 0$ . Calcule el campo en todos los puntos del espacio.

Para el sistema de los dos planos, calcule la diferencia de potencial entre el plano cargado positivamente y el cargado negativamente.

1.8 Dos planos cargados oblicuos

Se tiene una distribución de cargas formada por dos planos de gran extensión situados perpendicularmente al plano OXY tal como indica la figura (la cuadrícula tiene un espaciado $b$ ). El ángulo θ es tal que tg⁡(θ)=4/3. Uno de los planos almacena una densidad de carga uniforme $+ σ 0$ y el otro una densidad de carga $- σ 0$ .

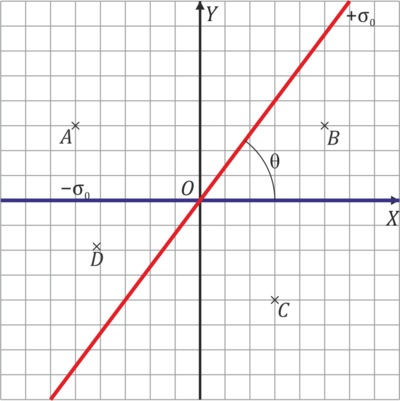
Halle el campo eléctrico en los puntos A, B, C y D.
Calcule el potencial eléctrico en los mismos puntos tomando como origen de potencial el origen de coordenadas O.
Además de los planos cargados se colocan dos cargas puntuales $+ q$ en los puntos A y B. Halle la fuerza eléctrica sobre cada una de ellas.

1.9 Campo eléctrico de un segmento

Calcule el campo eléctrico producido por un segmento rectilíneo cargado uniformemente con una densidad de carga $λ 0$ en cualquier punto del plano perpendicular al segmento por su punto medio.

A partir del resultado anterior, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea $λ 0$ .

1.10 Potencial eléctrico debido a una superficie esférica

Halle el potencial eléctrico en todos los puntos del espacio creado por una carga $Q$ distribuida uniformemente sobre una superficie esférica de radio $R$ .

1.11 Potencial eléctrico debido a una esfera maciza

Halle, a partir del campo eléctrico, el potencial eléctrico debido a una esfera de radio R que almacena una carga Q distribuida uniformemente en su volumen.

Para el centro de la esfera, calcule el potencial eléctrico por integración directa. Compruebe que el resultado coincide con el interior para este punto.

1.12 Potencial eléctrico en el eje de un anillo

Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia $z$ al plano del anillo.

¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo?

Supongamos que en lugar de una carga positiva tenemos una de −2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia 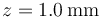$z= 1.0\,\mathrm{mm}$ del centro del anillo, ¿qué tipo de movimiento describe esta carga?

1.13 Energía electrostática de un sistema de cargas puntuales

Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales:

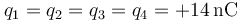$q_1=q_2=q_3=q_4=+14\,\mathrm{nC}$ .
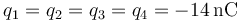$q_1=q_2=q_3=q_4=-14\,\mathrm{nC}$ .
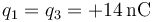$q_1=q_3=+14\,\mathrm{nC}$ , $q_2=q_4=-14\,\mathrm{nC}$ .
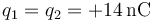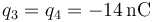$q_1=q_2=+14\,\mathrm{nC}$ , $q_3=q_4=-14\,\mathrm{nC}$ .
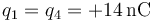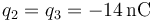$q_1=q_4=+14\,\mathrm{nC}$ , $q_2=q_3=-14\,\mathrm{nC}$ .

situadas en cada caso en los vértices de un rectángulo

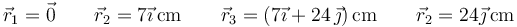
$\vec{r}_1 = \vec{0}\qquad \vec{r}_2 = 7\vec{\imath}\,\mathrm{cm}\qquad \vec{r}_3 = (7\vec{\imath}+24\,\vec{\jmath})\,\mathrm{cm}\qquad \vec{r}_2 = 24\vec{\jmath}\,\mathrm{cm}$

1.14 Energía electrostática de superficies esféricas

Calcule la energía electrostática almacenada en las siguientes distribuciones de carga:

Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga $Q$ .
Dos superficies esféricas concéntricas de radios $a$ y $b$ ( $a < b$ ) sobre las cuales hay distribuidas uniformemente cargas $+ Q$ y $- Q$ respectivamente.
Dos superficies esféricas concéntricas de radios $a$ y $b$ ( $a < b$ ) sobre las cuales hay distribuidas cargas con densidades $+ σ 0$ y $- σ 0$ respectivamente.
Tres superficies esféricas concéntricas de radios 2𝑏, 3𝑏 y 6𝑏, que almacenan, respectivamente, cargas $1$ , $2$ y $3$ . ¿A qué se reduce el resultado si $Q 1 = Q 3 = Q 0$ , $Q 2 = - Q 0$ ?

1.15 Dos esferas cargadas adyacentes

Dos esferas de radio $R$ están cargadas uniformemente en su volumen con una carga $Q$ cada una. Las dos esferas son adyacentes, de forma que sus centros se hallan en 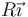$±R\vec{\imath}$ .

Calcule el campo eléctrico en los puntos $A ( - R,0)$ , $B ( + R,0)$ , $C (0,4 R 3)$ , $D ( - 8 R 3,0)$ y $F ( - 3 R 2,0)$ . El campo en todos estos puntos puede escribirse en la forma

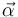$\vec{E}=\frac{Q}{4\pi\varepsilon_0 R^2}\vec{\alpha}⃗$

con $\vec{\alpha}$ un cierto coeficiente vectorial distinto para cada punto, que es el que hay que determinar.

Calcule el trabajo necesario para mover una cierta carga puntual $q$ desde el punto A al punto B, si la carga se desplaza lentamente a lo largo del segmento rectilíneo indicado.
Calcule el trabajo necesario para mover la misma carga puntual $q$ desde el punto C al punto D, si la carga se desplaza lentamente a lo largo del camino quebrado que se indica.

2 Problemas adicionales

2.1 Esfera cargada con hueco relleno

Una esfera de radio $2 R$ posee un hueco también esférico de radio R cuyo centro se encuentra a una distancia $R$ del centro de la esfera grande. La esfera grande almacena una carga $+ 7 q 0$ distribuida uniformemente en su volumen, mientras que en el hueco hay una carga $- 7 q 0$ también distribuida uniformemente.

Halle el campo eléctrico en los puntos O, B, C, A y D marcados en la figura. A es el centro de la esfera negativa y D es equidistante de O y A.
Calcule el trabajo para mover una carga puntual q desde el punto B al punto C, diametralmente opuesto.
Calcule el trabajo para mover la misma carga desde el punto B hasta el punto O.
En puntos exteriores a la esfera y alejados de ella, el sistema se ve como un dipolo. ¿Cuánto vale el momento dipolar eléctrico de este dipolo?

2.2 Cálculos a partir de un campo eléctrico

El valor de un campo eléctrico en todos los puntos del espacio viene dado por

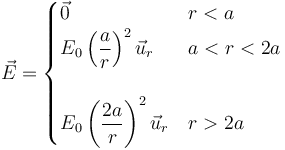
$\vec{E}=\begin{cases} \vec{0} & r < a \\ E_0\left(\displaystyle\frac{a}{r}\right)^2\vec{u}_r & a < r < 2a \\ & \\ E_0\left(\displaystyle\frac{2a}{r}\right)^2\vec{u}_r & r > 2a \end{cases}$

siendo $r$ la distancia al origen de coordenadas y 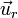$\vec{u}_r$ el vector unitario radial hacia afuera.

Calcule las densidades de carga que causan este campo.
¿Cuánto vale la carga total de la distribución?
Halle el potencial eléctrico en $r = 0$ , en $r = a$ y en $r = 2 a$ , tomando como origen de potencial el infinito.
Calcule la energía electrostática almacenada en este sistema.

2.3 Sistema de tres superficies esféricas cargadas

Supongamos un sistema formado por tres superficies esféricas concéntricas, de radios $R 1 = 2 a$ , $R 2 = 3 a$ y $R 3 = 6 a$ , respectivamente, que almacenan cargas $Q 1$ , $Q 2$ y $Q 3$ distribuidas uniformemente en cada una.

Calcule

El campo eléctrico en todos los puntos del espacio.
El trabajo necesario para llevar una carga $q 0$ desde el infinito hasta el centro del sistema.
La energía electrostática almacenada en el sistema de tres esferas (sin incluir la carga $q 0$ ).

para cada uno de los siguientes tres casos:

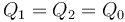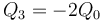$Q_1=Q_2=Q_0\,$ , $Q_3=-2Q_0\,$ .
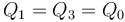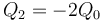$Q_1=Q_3=Q_0\,$ , $Q_2=-2Q_0\,$ .
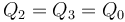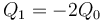$Q_2=Q_3=Q_0\,$ , $Q_1=-2Q_0\,$ .

2.4 Carga distribuida en un anillo

Un anillo de radio R se encuentra en el plano OXY con centro el origen de coordenadas. El anillo almacena una distribución de carga con densidad lineal

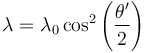
$\lambda=\lambda_0\cos^2\left(\frac{\theta'}{2}\right)$

siendo θ' el ángulo que forma con el eje OX el vector de posición de los puntos del anillo. Para esta distribución, halle

La carga total almacenada
El potencial eléctrico en el origen de coordenadas
El campo eléctrico en el origen de coordenadas.

2.5 Comparación del campo de dos cargas

Considere las dos situaciones siguientes:

Una carga +20 nC situada en el origen de coordenadas.
Dos cargas de +10 nC situadas en 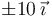$\pm 10\,\vec{\imath}$ (cm)

Para cada una de estas dos situaciones, halle:

El campo eléctrico en los puntos 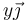$y\vec{\jmath}$ con y = 0, 5, 10, 20, 50 y 100cm. ¿Cuánto vale, en cada caso, el error relativo cometido al sustituir las dos cargas puntuales por una sola, de doble valor, situada en el origen?
Repita el cálculo para el potencial eléctrico en los mismos puntos.

2.6 Fuerza eléctrica debida a un potencial definido a trozos

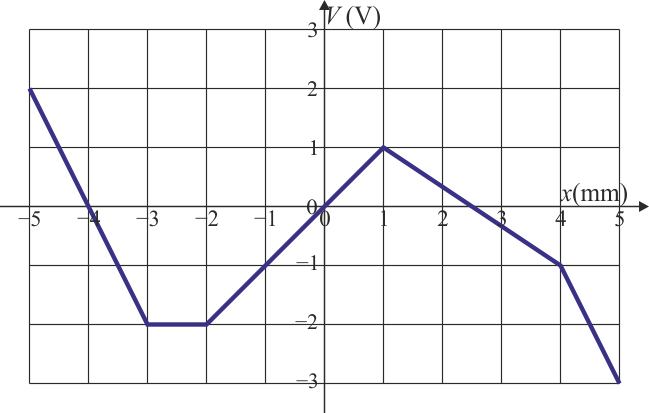
Considere que el potencial eléctrico a lo largo del eje $X$ viene dado por la gráfica de la figura. Indique el sentido de la fuerza sobre una carga positiva sometida a este potencial. ¿Dónde es máxima esta fuerza en módulo? Si la carga se suelta en reposo en $x = 0$ , ¿qué tipo de movimiento describe?

¿Cómo cambian los resultados si la carga es negativa?

3 Preguntas de test

3.1 Flujo de cuatro cargas en un cuadrado

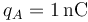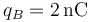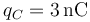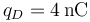Se tienen cuatro cargas en los vértices consecutivos de un cuadrado ABCD de lado $a=10\,\mathrm{cm}$ , siendo sus valores $q_A = 1\,\mathrm{nC}$ , $q_B=2\,\mathrm{nC}$ , $q_C=3\,\mathrm{nC}$ , $q_D=4\,\mathrm{nC}$ . ¿Cuánto vale el flujo del campo eléctrico multiplicado por $\varepsilon_0$ a través de una esfera centrada en la primera carga y de radio 12 cm?

A 6 nC
B 1 nC
C 10 nC
D 7 nC

3.2 Fuerza de cuatro cargas en un cuadrado

Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide 20 cm, según ilustra la figura. Los valores de todas las cargas son +10 nC o $-$ 10 nC

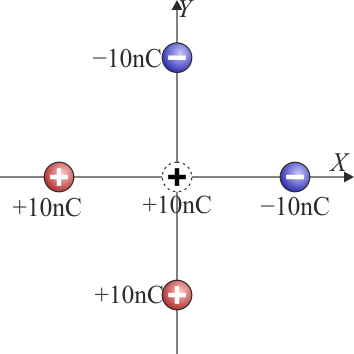
¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado?

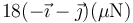
A $18(-\vec{\imath}-\vec{\jmath})(\mu\mathrm{N})$
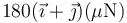
B $180(\vec{\imath}+\vec{\jmath})(\mu\mathrm{N})$
C Es nula
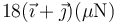
D $18(\vec{\imath}+\vec{\jmath})(\mu\mathrm{N})$

¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito?

A No hay información suficiente para hallarlo.
B −36 $μ$ J.
C +36 μJ.
D Es nulo.

Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema?

A Es nula.
B −9 μJ.
C +9 μJ.
D No hay información suficiente para hallarla.

3.3 Distribución de carga en esfera

Se tiene únicamente una distribución uniforme de una carga $Q < 0$ sobre una superficie esférica de radio $a$ . Para los tres puntos de la figura,

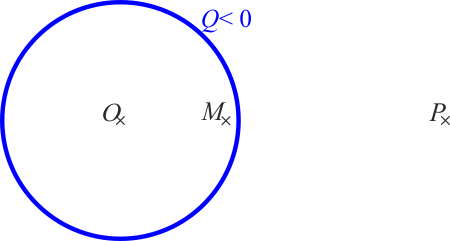
¿En cuál es mayor en módulo el campo eléctrico?

A En M.
B En O.
C No hay información suficiente para saberlo.
D En P.

¿Cómo se ordena el potencial de los tres puntos?

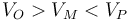A $V_O > V_M < V_P\,$ .
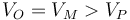B $V_O = V_M > V_P\,$ .
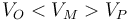C $V_O < V_M > V_P\,$ .
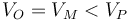D $V_O = V_M < V_P\,$ .

3.4 Energía de dos cargas

Dos cargas puntuales positivas $q 1$ y $q 2$ se encuentran a una distancia $a$ . Si la distancia entre ellas se reduce a la mitad, ¿cómo cambia la energía electrostática del sistema?

A Aumenta al cuádruple
B Se reduce a la mitad.
C Aumenta al doble.
D No cambia.

3.5 Cargas en una barra

En los dos extremos de una barra rígida se encuentran cargas de la misma magnitud y signo opuesto. La barra se encuentra inicialmente en reposo y sumergida en un campo eléctrico uniforme, formando un cierto ángulo con el campo. ¿Qué efecto produce el campo sobre la barra?

A Ninguno. Las fuerzas se cancelan y la barra permanece en reposo.
B Produce un par de fuerzas que tiende a alinear la barra con el campo.
C Produce un par de fuerzas que tiende a colocar la barra perpendicular al campo.
D Produce una fuerza neta que tiende a desplazar la barra.

3.6 Esfera cargada en volumen y superficie

Se tiene una distribución de carga formada por una esfera de radio $b$ cargada uniformemente con una densidad volumétrica de carga $ρ 0$ , Esta esfera está forrada por una superficie esférica (también de radio $b$ ) con densidad de carga superficial $σ 0$ , de tal forma que la carga total del sistema es nula.

¿Cuánto vale $σ 0$ ?

A $- ρ 0 b$
B $- ρ 0$
C $- 4π b 2 ρ 0$
D $- ρ 0 b / 3$

Para esta distribución de carga, ¿cuánto vale el campo eléctrico que produce?

A Es nulo en el interior de la esfera y vale 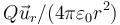$Q\vec{u}_r/(4\pi\varepsilon_0 r^2)$ en el exterior con $Q = (4π b 3 / 3)ρ 0$ .
B Es nulo en el interior de la esfera y vale 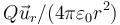$Q\vec{u}_r/(4\pi\varepsilon_0 r^2)$ en el exterior con $Q = (4π b 2)σ 0$ .
C Es nulo en todos los puntos del espacio.
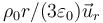D Es nulo en el exterior de la esfera y vale $\rho_0 r/(3\varepsilon_0)\vec{u}_r$ en el interior.

Para este sistema, ¿cuánto vale el potencial eléctrico en el centro de la esfera?

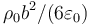A $\rho_0 b^2/(6\varepsilon_0)$ ,
B Es nulo.
C Tiende a infinito.
D 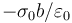$-\sigma_0 b/\varepsilon_0$ .

3.7 Campo de dos cargas

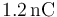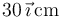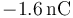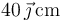Una carga puntual de valor $1.2\,\mathrm{nC}$ se encuentra situada en el punto $30\,\vec{\imath}\,\mathrm{cm}$ y una de valor $-1.6\,\mathrm{nC}$ en $40\,\vec{\jmath}\,\mathrm{cm}$ .

¿Cuánto vale, en módulo, el campo en 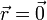$\vec{r}=\vec{0}$ ?

A 30 V/m
B 150 V/m
C 210 V/m
D −30 V/m

¿Y el potencial eléctrico en el mismo punto 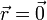$\vec{r}=\vec{0}$ ?

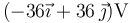
A $(-36\vec{\imath}+36\,\vec{\jmath})\mathrm{V}$
B 72 V.
C 210 V.
D 0 V.

3.8 Definición de franklin

Un franklin es una unidad de carga eléctrica definida como aquella tal que dos cargas de 1 franklin situadas a 1 cm se ejercen una fuerza de 1 dina ( $= 10 - 5 N$ ). ¿A cuantos culombios equivale un franklin?

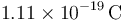
A $1.11\times 10^{-19}\,\mathrm{C}$
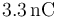
B $3.3\,\mathrm{nC}$
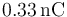
C $0.33\,\mathrm{nC}$
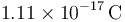
D $1.11\times 10^{-17}\,\mathrm{C}$

3.9 Sentido del campo eléctrico

Dada una cierta distribución de potencial eléctrico, el campo eléctrico apunta en el sentido…

A en que decrece el potencial.
B tangente a las superficies equipotenciales.
C en que crece o decrece el potencial, dependiendo de donde estén las cargas eléctricas.
D en que crece el potencial.

3.10 Esferas concéntricas

Se tienen dos superficies esféricas concéntricas de radios $a$ y $2 a$ , centradas en el origen de coordenadas. La interior está cargada con una densidad superficial uniforme $+ σ 0$ y la exterior con una $- σ 0$ .

El campo eléctrico en un punto a 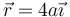$\vec{r}=4a\vec{\imath}$ vale

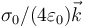
A $\sigma_0/(4\varepsilon_0)\vec{k}$
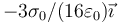
B $-3\sigma_0/(16\varepsilon_0)\vec{\imath}$
C $\vec{0}$
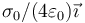
D $\sigma_0/(4\varepsilon_0)\vec{\imath}$

Para este sistema el potencial en el origen de coordenadas vale\ldots

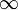
A $\infty$
B 0
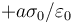
C $+a\sigma_0/\varepsilon_0$
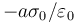
D $-a\sigma_0/\varepsilon_0$

3.11 Fuerza sobre una carga en movimiento

Una carga puntual se mueve en el seno de un campo eléctrico 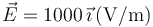$\vec{E}=1000\,\vec{\imath}\,(\mathrm{V}/\mathrm{m})$ y de un campo magnético 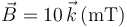$\vec{B}=10\,\vec{k}\,(\mathrm{mT})$ . ¿Con qué velocidad debe moverse la carga para que la fuerza electromagnética sobre ella sea nula?

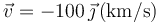
A $\vec{v}=-100\,\vec{\jmath}\,(\mathrm{km}/\mathrm{s})$
B Es imposible que se anule la fuerza.
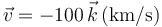
C $\vec{v}=-100\,\vec{k}\,(\mathrm{km}/\mathrm{s})$
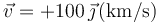
D $\vec{v}=+100\,\vec{\jmath}\,(\mathrm{km}/\mathrm{s})$

3.12 Acción de dos cargas sobre una tercera

Se tiene un sistema formado por tres cargas puntuales de valores $+ q$ , $+ q$ y $+ 2 q$ situadas en las posiciones de la figura.

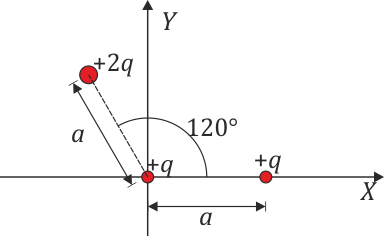
Si llamamos 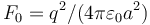$F_0=q^2/(4\pi\varepsilon_0a^2)$ , la fuerza sobre la carga situada en el origen es igual a

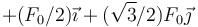
A $+(F_0/2)\vec{\imath}+(\sqrt{3}/2)F_0\vec{\jmath}$
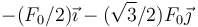
B $-(F_0/2)\vec{\imath}-(\sqrt{3}/2)F_0\vec{\jmath}$
C $\vec{0}$
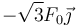
D $-\sqrt{3}F_0\vec{\jmath}$

¿Qué trabajo es necesario realizar por un agente externo para llevar la carga cuasiestáticamente del origen de coordenadas hasta el infinito?

A $- 3 F 0 a$ .
B Es nulo.
C Es infinito.
D $+ 3 F 0 a$ .

3.13 Dos cargas desiguales

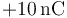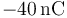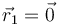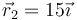Se tienen dos cargas $+10\,\mathrm{nC}$ y $-40\,\mathrm{nC}$ situadas respectivamente en $\vec{r}_1=\vec{0}$ y $\vec{r}_2=15\vec{\imath}$ (cm).

¿En qué punto se anula el campo eléctrico debido a las dos cargas? (en cm)

A No se anula en ningún punto.
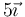
B $5\vec{\imath}$
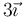
C $3\vec{\imath}$
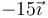
D $-15\vec{\imath}$

¿En qué punto se anula el potencial eléctrico, si el origen de potencial está en el infinito?

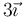
A $3\vec{\imath}$
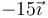
B $-15\vec{\imath}$
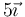
C $5\vec{\imath}$
D No se anula en ningún punto.

3.14 Campo eléctrico radial

En una región del espacio el campo eléctrico es radial desde el origen de coordenadas 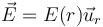$\vec{E}=E(r)\vec{u}_r$ , dependiendo de la distancia al centro según la gráfica

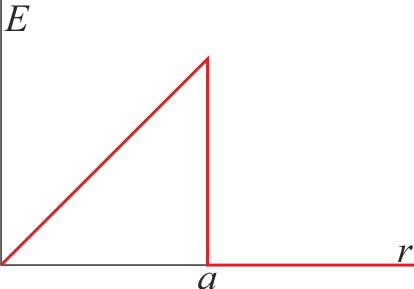
¿Cómo es la densidad de carga que produce este campo?

A Solo una esfera cargada uniformemente con una densidad positiva.
B Una esfera cargada uniformemente con una densidad positiva, recubierta de una superficie negativa.
C No hay información suficiente para saberlo.
D Una esfera cargada con una densidad que aumenta al alejarnos del centro.

Problemas de electrostática en el vacío (GIE)