Sistema de tres superficies esféricas cargadas

De Laplace

Contenido

1 Enunciado
2 Campo eléctrico
3 Trabajo
4 Energía almacenada
- 4.1 A partir de la carga y el potencial
- 4.2 A partir de la densidad de energía

1 Enunciado

Supongamos un sistema formado por tres superficies esféricas concéntricas, de radios $R 1 = 2 a$ , $R 2 = 3 a$ y $R 3 = 6 a$ , respectivamente, que almacenan cargas $Q 1$ , $Q 2$ y $Q 3$ distribuidas uniformemente en cada una.

Calcule

El campo eléctrico en todos los puntos del espacio.
El trabajo necesario para llevar una carga $q 0$ desde el infinito hasta el centro del sistema.
La energía electrostática almacenada en el sistema de tres esferas (sin incluir la carga $q 0$ ).

para cada uno de los siguientes tres casos:

$Q 1 = Q 2 = Q 0$ , $Q 3 = - 2 Q 0$ .
$Q 1 = Q 3 = Q 0$ , $Q 2 = - 2 Q 0$ .
$Q 2 = Q 3 = Q 0$ , $Q 1 = - 2 Q 0$ .

2 Campo eléctrico

En lugar de resolver tres veces el mismo problema, consideramos un sistema con cargas cualesquiera y posteriormente sustituimos por sus valores concretos.

El campo debido a las tres esferas, se calcula por aplicación de la ley de Gauss. Por la simetría esférica del sistema, el campo es radial y dependiente solo de la distancia al centro del sistema

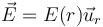
$\vec{E}=E(r)\vec{u}_r$

Para cada superficie esférica que tomemos

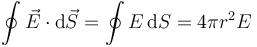
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\oint E\,\mathrm{d}S = 4\pi r^2E$

De acuerdo con la ley de Gauss

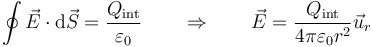
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}\qquad\Rightarrow\qquad \vec{E}=\frac{Q_\mathrm{int}}{4\pi \varepsilon_0 r^2}\vec{u}_r$

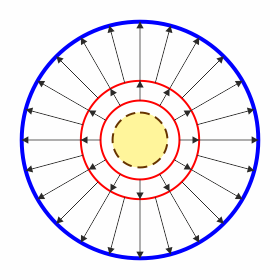
Tenemos ahora cuatro regiones, de adentro a fuera:

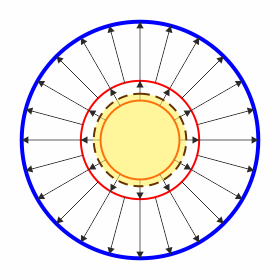
r<2a	2a<r<3a

3a<r<6a	6a<r

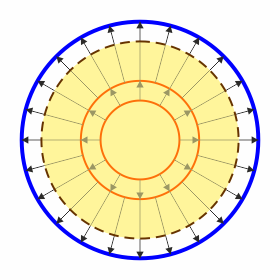
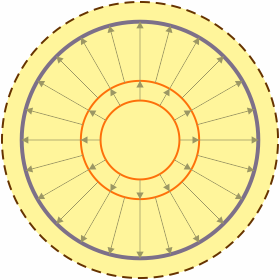
r < 2a: En el interior de la esfera pequeña no se envuelve ninguna carga, por lo que el campo es nulo

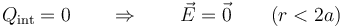
$Q_\mathrm{int}=0\qquad\Rightarroçw\qquad \vec{E}=\vec{0}\qquad (r< 2a)$

2a < r < 3a: Entre la esfera pequeña y la intermedia se envuelve a la esfera pequeña, con carga $Q 1$

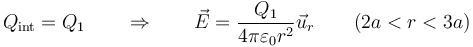
$Q_\mathrm{int}=Q_1\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (2a < r < 3a)$

3a < r < 6a: Entre la esfera intermedia y la grande se envuelve tanto a la esfera pequeña como a la intermedia

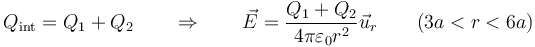
$Q_\mathrm{int}=Q_1+Q_2\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1+Q_2}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (3a < r < 6a)$

6a<r: En el exterior de la esfera grande se envuelve a las tres esferas

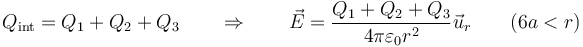
$Q_\mathrm{int}=Q_1+Q_2+Q_3\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1+Q_2+Q_3}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (6a < r)$

Ahora bien, en los tres casos prácticos, la suma de las tres cargas es cero, así que

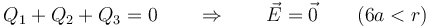
$Q_1 + Q_2 + Q_3 = 0 \qquad\Rightarroçw\qquad \vec{E}=\vec{0}\qquad (6a< r)$

Reuniendo los cuatro resultados

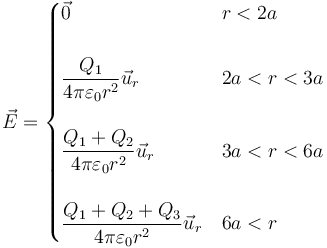
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_1}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{Q_1+Q_2}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \displaystyle \frac{Q_1+Q_2+Q_3}{4\pi \varepsilon_0 r^2}\vec{u}_r & 6a < r\end{cases}$

Primer caso: Sustituimos ahora los valores de $Q 1$ y $Q 2$ . En el primer caso

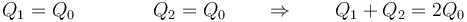
$Q_1 = Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=2Q_0$

lo que nos da el campo

$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

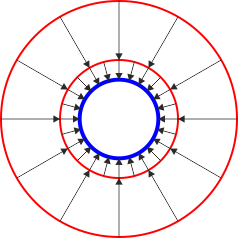
El campo va hacia afuera en las dos regiones en que no es nulo.

Segundo caso: En el segundo caso

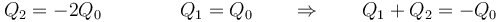
$Q_2 = -2Q_0\qquad\qquad Q_1=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0$

que aplicado al campo da

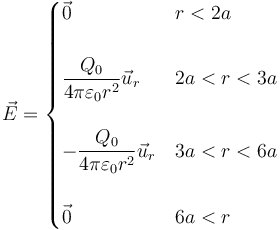
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

En la región entre la esfera intermedia y la exterior va ahora hacia adentro.

Tercer caso: Por último

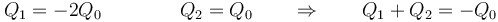
$Q_1 = -2Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0$

lo que nos da ahora el campo

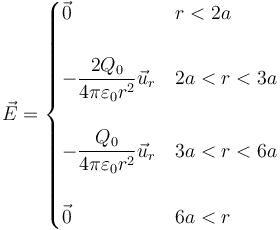
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle -\frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

En este caso el campo va ahora hacia adentro en las dos regiones en que no es nulo.

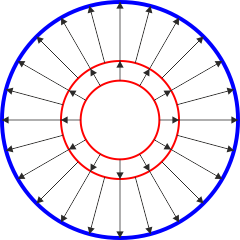
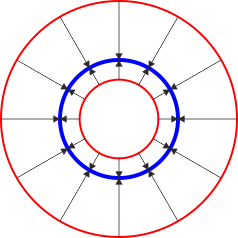
Primer caso	Segundo caso	Tercer caso

3 Trabajo

El trabajo para llevar una carga $q 0$ desde el infinito hasta el centro C del sistema puede calcularse mediante la integral

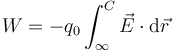
$W = -q_0\int_\infty^C \vec{E}\cdot\mathrm{d}\vec{r}$

Esta integral equivale al producto de la carga por la diferencia de potencial

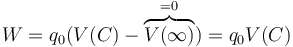
$W = q_0(V(C)-\overbrace{V(\infty)}^{=0})=q_0V(C)$

El potencial en el punto C es la suma de los que crean las tres esferas. El potencial debido a una superficie esférica de radio $R$ cargada uniformemente con una carga $Q$ vale

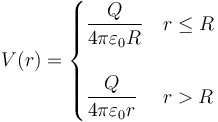
$V(r) = \begin{cases}\displaystyle \frac{Q}{4\pi\varepsilon_0R} & r \leq R \\ & \\ \displaystyle \frac{Q}{4\pi\varepsilon_0r} & r > R \end{cases}$

El centro del sistema es interior a las tres esferas, así que

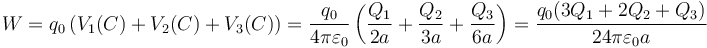
$W = q_0\left(V_1(C)+V_2(C)+V_3(C)\right)=\frac{q_0}{4\pi\varepsilon_0}\left(\frac{Q_1}{2a}+\frac{Q_2}{3a}+\frac{Q_3}{6a}\right)=\frac{q_0(3Q_1+2Q_2+Q_3)}{24\pi\varepsilon_0 a}$

Sustituyendo obtenemos las tres soluciones siguientes

Primer caso: Tenemos que $Q 1 = Q 2 = Q 0$ , $Q 3 = - 2 Q 0$ , que sustituido da

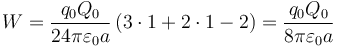
$W = \frac{q_0Q_0}{24\pi\varepsilon_0 a}\left(3\cdot 1+2\cdot 1-2\right)=\frac{q_0Q_0}{8\pi\varepsilon_0a}$

Segundo caso: Ahora $Q 1 = Q 3 = Q 0$ , $Q 2 = - 2 Q 0$ , y el trabajo vale

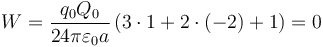
$W = \frac{q_0Q_0}{24\pi\varepsilon_0 a}\left(3\cdot 1+2\cdot (-2)+1\right)=0$

Tercer caso: Por último $Q 2 = Q 3 = Q 0$ , $Q 1 = - 2 Q 0$ , resultando el trabajo

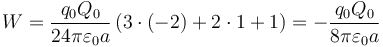
$W = \frac{q_0Q_0}{24\pi\varepsilon_0 a}\left(3\cdot(-2)+2\cdot 1+1\right)=-\frac{q_0Q_0}{8\pi\varepsilon_0a}$

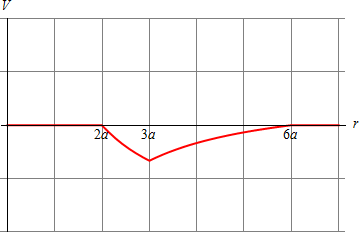
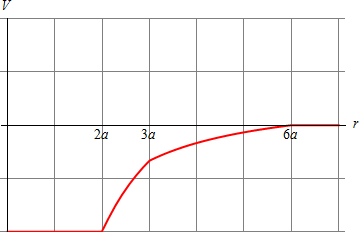
Vemos que en el primer caso resulta un trabajo positivo, es decir, equivale a que para traer la carga hay que “subir una montaña”; en el segundo caso es nulo, porque primero se desciende y luego se vuelve a subir en la misma cantidad; en el último caso el trabajo es negativo, ya que solo se desciende. Esto se entiende fácilmente observando el sentido del campo en cada uno de los tres casos. En el primero siempre va hacia afuera, por lo que se opone en todo momento al acercamiento de la carga; en el segundo primero (visto desde el exterior, desde donde nos acercamos) va hacia adentro, ayudando al acercamiento, pero luego se opone; en el último caso siempre va hacia adentro, por lo que siempre ayuda a que la carga vaya hacia el centro.

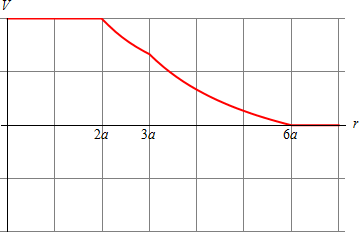
Primer caso	Segundo caso	Tercer caso

El trabajo también se puede hallar mediante la integral de camino del campo eléctrico indicada al principio. Esta se descompone en cuatro tramos

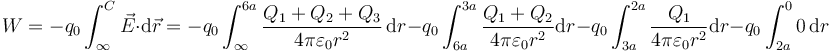
$W = -q_0\int_{\infty}^C\vec{E}\cdot\mathrm{d}\vec{r}=-q_0\int_\infty^{6a}\frac{Q_1+Q_2+Q_3}{4\pi\varepsilon_0 r^2}\,\mathrm{d}r-q_0\int_{6a}^{3a}\frac{Q_1+Q_2}{4\pi\varepsilon_0 r^2}\mathrm{d}r-q_0\int_{3a}^{2a}\frac{Q_1}{4\pi\varepsilon_0r^2}\mathrm{d}r -q_0\int_{2a}^0 0\,\mathrm{d}r$

Cada una de estas integrales es del tipo

$\int_{a}^b \frac{\mathrm{d}r}{r^2}=\left.-\frac{1}{r}\right|_a^b = \frac{1}{a}-\frac{1}{b}$

por lo que resulta el trabajo

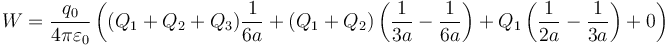
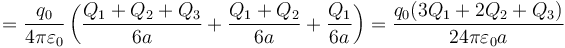
$W = \frac{q_0}{4\pi\varepsilon_0}\left((Q_1+Q_2+Q_3)\frac{1}{6a}+(Q_1+Q_2)\left(\frac{1}{3a}-\frac{1}{6a}\right)+Q_1\left(\frac{1}{2a}-\frac{1}{3a}\right)+0\right)$ $=\frac{q_0}{4\pi\varepsilon_0}\left(\frac{Q_1+Q_2+Q_3}{6a}+\frac{Q_1+Q_2}{6a}+\frac{Q_1}{6a}\right)=\frac{q_0(3Q_1+2Q_2+Q_3)}{24\pi\varepsilon_0 a}$

que coincide naturalmente con el resultado obtenido previamente.

4 Energía almacenada

4.1 A partir de la carga y el potencial

Dada una distribución de carga superficial, la energía electrostática almacenada en el sistema se puede calcular mediante la integral

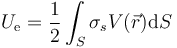
$U_\mathrm{e}=\frac{1}{2}\int_S \sigma_s V(\vec{r})\mathrm{d}S$

En este caso, que tenemos tres superficies cargadas, la energía se descompone en suma de tres integrales

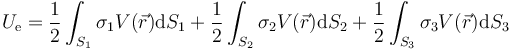
$U_\mathrm{e}=\frac{1}{2}\int_{S_1} \sigma_1 V(\vec{r})\mathrm{d}S_1+\frac{1}{2}\int_{S_2} \sigma_2 V(\vec{r})\mathrm{d}S_2+\frac{1}{2}\int_{S_3} \sigma_3 V(\vec{r})\mathrm{d}S_3$

En este caso y debido a la simetría esférica, el potencial eléctrico (que depende solo de la distancia al centro del sistema) es constante en cada superficie, por lo que puede salir de cada integral.

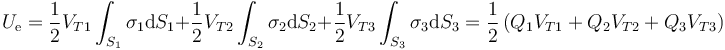
$U_\mathrm{e}=\frac{1}{2}V_{T1}\int_{S_1} \sigma_1\mathrm{d}S_1+\frac{1}{2}V_{T2}\int_{S_2} \sigma_2 \mathrm{d}S_2+\frac{1}{2}V_{T3}\int_{S_3} \sigma_3 \mathrm{d}S_3=\frac{1}{2}\left(Q_1V_{T1}+Q_2V_{T2}+Q_3V_{T3}\right)$

donde hemos añadido “T” al subíndice para indicar que ese potencial es debido a las tres esferas y no solo a cada una de ellas.

La esfera interior coincide consigo misma y está en el interior de las otras dos, por lo que su potencial valr

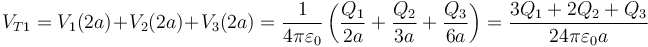
$V_{T1}=V_1(2a) + V_2(2a)+V_3(2a) = \frac{1}{4\pi\varepsilon_0}\left(\frac{Q_1}{2a}+\frac{Q_2}{3a}+\frac{Q_3}{6a}\right)=\frac{3Q_1+2Q_2+Q_3}{24\pi\varepsilon_0 a}$

La esfera intermedia se encuentra en el exterior de la pequeña y en el interior de la grande,

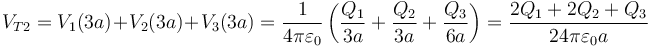
$V_{T2}=V_1(3a) + V_2(3a)+V_3(3a) = \frac{1}{4\pi\varepsilon_0}\left(\frac{Q_1}{3a}+\frac{Q_2}{3a}+\frac{Q_3}{6a}\right)=\frac{2Q_1+2Q_2+Q_3}{24\pi\varepsilon_0 a}$

(cambia el 2 por un 3 en el denominador porque ahora debemos usar la fórmula con $1 / r$ , haciendo $r = 3 a$ ).

La esfera exterior está en el exterior de las otras dos

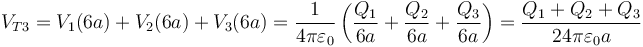
$V_{T3}=V_1(6a) + V_2(6a)+V_3(6a) = \frac{1}{4\pi\varepsilon_0}\left(\frac{Q_1}{6a}+\frac{Q_2}{6a}+\frac{Q_3}{6a}\right)=\frac{Q_1+Q_2+Q_3}{24\pi\varepsilon_0 a}$

Este potencial va a ser nulo en todos los casos, ya que la suma de las tres cargas es 0.

Sustituimos en la expresión de la energía

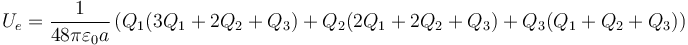
$U_e=\frac{1}{48\pi\varepsilon_0a}\left(Q_1(3Q_1+2Q_2+Q_3)+Q_2(2Q_1+2Q_2+Q_3)+Q_3(Q_1+Q_2+Q_3)\right)$

Puesto que en todos los casos prácticos $Q 3 = - Q 1 - Q 2$ esta fórmula se puede reducir a

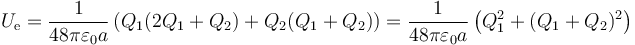
$U_\mathrm{e}=\frac{1}{48\pi\varepsilon_0a}\left(Q_1(2Q_1+Q_2)+Q_2(Q_1+Q_2)\right)=\frac{1}{48\pi\varepsilon_0a}\left(Q_1^2+(Q_1+Q_2)^2\right)$

Si aplicamos la fórmula completa a cada caso práctico

Primer caso: $Q 1 = Q 2 = Q 0$ , $Q 3 = - 2 Q 0$ y nos queda

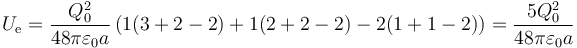
$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0 a}\left(1(3+2-2)+1(2+2-2)-2(1+1-2)\right)=\frac{5Q_0^2}{48\pi\varepsilon_0a}$

Segundo caso: $Q 1 = Q 3 = Q 0$ , $Q 2 = - 2 Q 0$ y nos queda

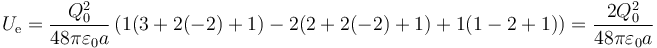
$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0 a}\left(1(3+2(-2)+1)-2(2+2(-2)+1)+1(1-2+1)\right)=\frac{2Q_0^2}{48\pi\varepsilon_0a}$

Tercer caso: $Q 2 = Q 3 = Q 0$ , $Q 1 = - 2 Q 0$ y nos queda

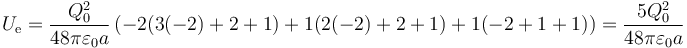
$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0 a}\left(-2(3(-2)+2+1)+1(2(-2)+2+1)+1(-2+1+1)\right)=\frac{5Q_0^2}{48\pi\varepsilon_0a}$

4.2 A partir de la densidad de energía

Esta energía también se puede calcular a partir de la densidad de energía

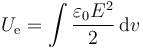
$U_\mathrm{e}=\int \frac{\varepsilon_0 E^2}{2}\,\mathrm{d}v$

En este caso dividimos el espacio en cuatro regiones e integramos en cada una de ellas. En cada región el campo es de la forma

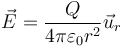
$\vec{E}=\frac{Q}{4\pi\varepsilon_0r^2}\vec{u}_r$

y la integral es sobre una corona esférica

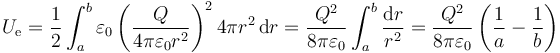
$U_\mathrm{e}=\frac{1}{2}\int_a^b\varepsilon_0\left(\frac{Q}{4\pi\varepsilon_0 r^2}\right)^2 4\pi r^2\,\mathrm{d}r= \frac{Q^2}{8\pi\varepsilon_0}\int_a^b \frac{\mathrm{d}r}{r^2}=\frac{Q^2}{8\pi\varepsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)$

El resultado total es

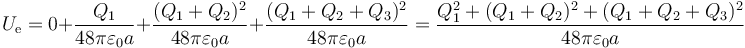
$U_\mathrm{e}=0+\frac{Q_1}{48\pi\varepsilon_0a}+\frac{(Q_1+Q_2)^2}{48\pi\varepsilon_0a}+\frac{(Q_1+Q_2+Q_3)^2}{48\pi\varepsilon_0a}=\frac{Q_1^2+(Q_1+Q_2)^2+(Q_1+Q_2+Q_3)^2}{48\pi\varepsilon_0a}$

que aplicado a los tres casos nos conduce a los mismos resultados

Primer caso

$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0a}\left(1^2+2^2+0^2\right)=\frac{5Q_0^2}{48\pi\varepsilon_0a}$

Segundo caso

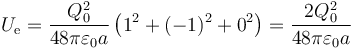
$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0a}\left(1^2+(-1)^2+0^2\right)=\frac{2Q_0^2}{48\pi\varepsilon_0a}$

Tercer caso

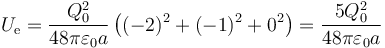
$U_\mathrm{e}=\frac{Q_0^2}{48\pi\varepsilon_0a}\left((-2)^2+(-1)^2+0^2\right)=\frac{5Q_0^2}{48\pi\varepsilon_0a}$

Vemos que en todos los casos resulta una energía positiva, como corresponde.

Sistema de tres superficies esféricas cargadas

De Laplace

Contenido

1 Enunciado

2 Campo eléctrico

3 Trabajo

4 Energía almacenada

4.1 A partir de la carga y el potencial

4.2 A partir de la densidad de energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES