Dos esferas huecas
De Laplace
Contenido |
1 Enunciado
Se tiene un sistema de cargas formado por dos superficies esféricas de radio 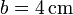 cuyos centros distan
cuyos centros distan 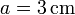 , como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de
, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de 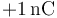 y
y 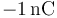
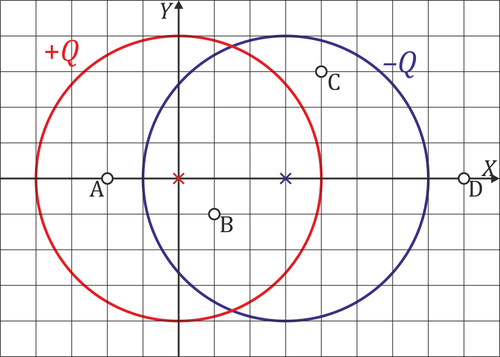
Para los puntos marcados en la figura (en cm)

- Calcule el campo eléctrico.
- Calcule el potencial eléctrico.
- A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de
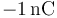 desde el punto A al punto D moviéndola a lo largo del eje X.
desde el punto A al punto D moviéndola a lo largo del eje X.
2 Campo eléctrico
La solución de este problema es una simple aplicación del principio de superposición. Basta con hallar el campo de cada superficie esférica y luego sumar las dos contribuciones.
El campo debido a una superficie esférica de radio acargada uniformemente tiene la expresión
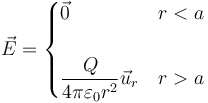
siendo r las distancia del punto de observación al centro de la esfera y 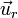 el vector unitario radial hacia afuera.
el vector unitario radial hacia afuera.
En todos los cálculos aparece el mismo factor
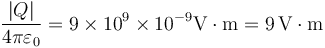
Así, tenemos para los cuatro puntos lo siguiente:
- Punto A
- Este punto está dentro de la esfera de carga positiva y fuera de la negativa. Para esta última la distancia al centro es de 5 cm y el vector unitario radial es
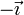 . Por tanto
. Por tanto
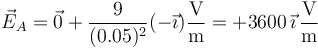
- Punto B
- Se encuentra en el interior de las dos esferas, por lo que
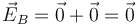
- Punto C
- Éste se halla dentro de la esfera de carga negativa y fuera de la positiva. La distancia al centro de esta es también de 5 cm, pero el unitario radial es ahora el que va en la dirección y sentido del vector
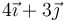
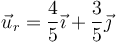
- lo que da el campo
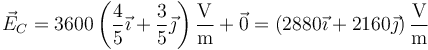
- Punto D
- Por último, este punto se encuentra fuera de las dos esferas, a 8 cm del centro de la esfera positiva y 5 de la negativa. El unitario radial es, en los dos casos
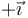 , lo que nos da
, lo que nos da
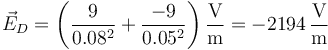
3 Potencial eléctrico
El cálculo para el potencial es análogo. Basta con sumar los potenciales debidos a cada esfera.
El potencial debido a una superficie esférica de radio a cargada uniformemente con una carga Q tiene la expresión
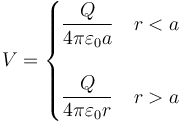
siendo el valor numérico del primer caso
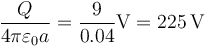
Esto nos da, para los cuatro puntos, siguiendo el mimso razonamiento que para el campo eléctrico
- Punto A
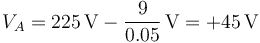
- Punto B
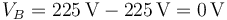
- Punto C
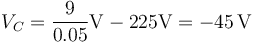
- Punto D
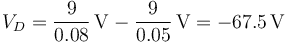
Podemos reunir estos resultados en una tabla
| Punto | 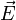 (V/m) (V/m)
| V (V) |
|---|---|---|
| A | 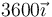
| +45 |
| B | 
| 0 |
| C | 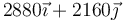
| −45 |
| D | 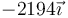
| −67.5 |
4 Trabajo
El trabajo para mover una carga puede hallarse a partir de la diferencia de potencial
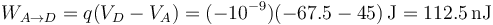
Sin embargo, aquí se trata de hallarlo a partir de la integración de la fuerza. En un proceso cuasiestático, la fuerza ejercida es opuesta a la eléctrica
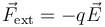
y el trabajo que queremos calcular será
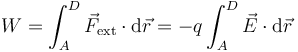
siendo
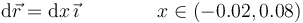
A la hora de hacer esta integral tenemos cuatro tramos, ya que el campo varía a lo largo del eje de manera discontinua. Si denotamos por x la posición sobre el eje, el campo en los puntos del eje será de la forma
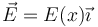
donde E(x) será positivo donde el campo vaya hacia la derecha (en el sentido de  ) y negativo donde vaya hacia la izquierda (en el sentido opuesto a
) y negativo donde vaya hacia la izquierda (en el sentido opuesto a  )
)
El campo de la esfera de carga positiva será, teniendo en cuenta que siempre es radial hacia afuera
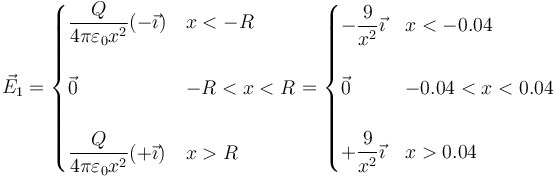
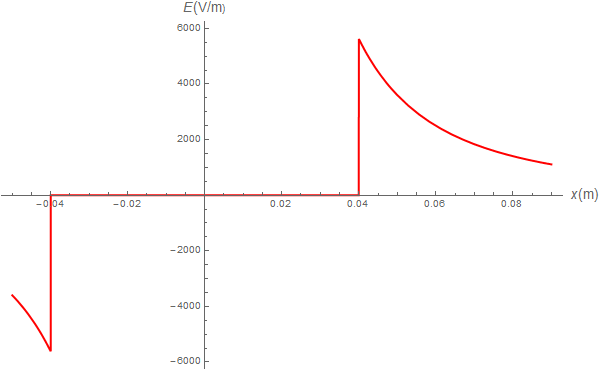
Para la esfera de carga negativa será similar, sin más que desplazar el centro de ésta y cambiar el signo
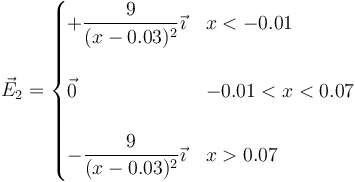
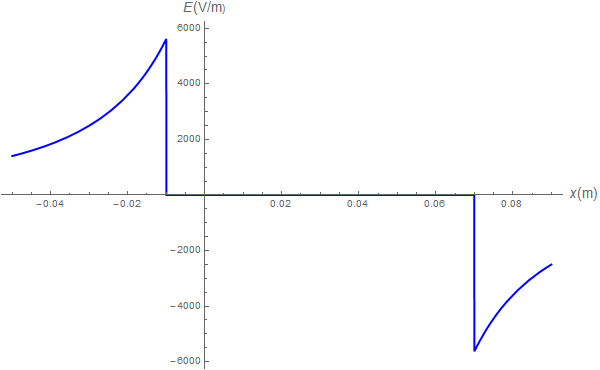
El campo total es la suma de estos dos
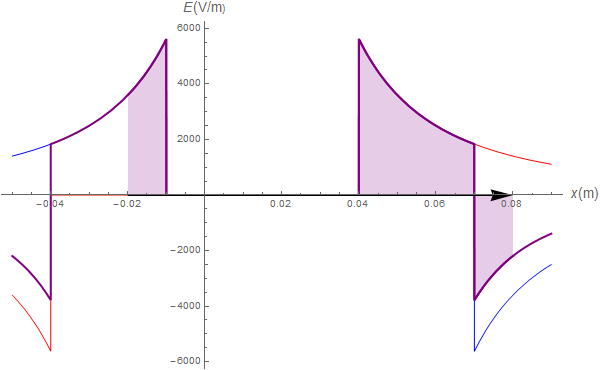
La integral va de 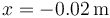 a
a 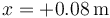 , por lo que debemos pasar por cuatro tramos.
, por lo que debemos pasar por cuatro tramos.
- Del punto A (x=−0.02) hasta la superficie cargada negativamente (x=−0.01)
- En este tramo el campo equivale al de una carga puntual situada en el centro de la esfera negativa
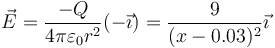
- ya que la distancia al centro de la esfera negativa es r = x − 0.03. El trabajo para recorrer este trozo es entonces
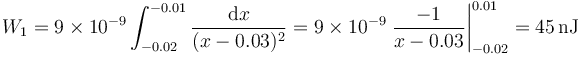
- Desde la superficie negativa (x=-0.01) hasta la positiva (x=0.04)
- En estre tramo el campo eléctrico se anula
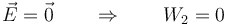
- Desde la superficie positiva (x=0.04) hasta la negativa (x=0.07)
- El campo es el de una carga puntual situada en el centro de la esfera positiva
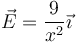
- siendo el trabajo
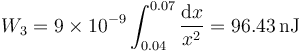
- Desde la superficie negativa (x=0.07) hasta D (x=0.08)
- Aquí el campo es suma del de dos cargas
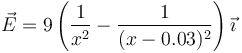
- siendo el trabajo
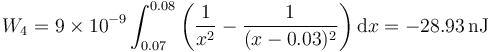
Sumando las cuatro contribuciones