Fuerza eléctrica debida a un potencial definido a trozos
De Laplace
1 Enunciado
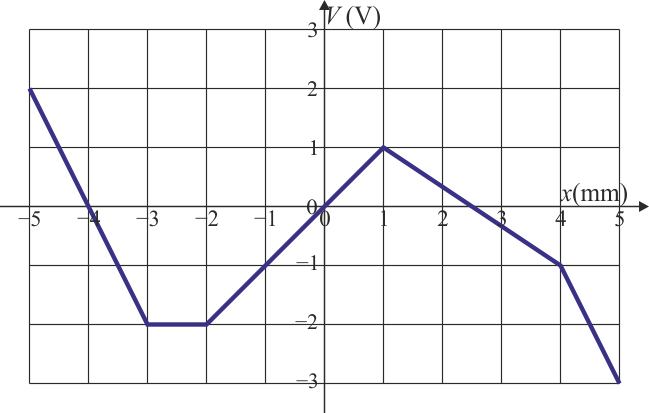
Considere que el potencial eléctrico a lo largo del eje X viene dado por la gráfica de la figura. Indique el sentido de la fuerza sobre una carga positiva de 1 μC sometida a este potencial. ¿Dónde es máxima esta fuerza en módulo? Si la carga se suelta en reposo en x = 0, ¿qué tipo de movimiento describe?
¿Cómo cambian los resultados si la carga es una negativa de −1μC?
2 Solución
El campo eléctrico debido a un potencial electrostático dado se calcula mediante el gradiente de éste
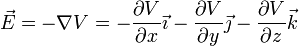
En el caso de un potencial que depende solo de la coordenada x, el gradiente se reduce a una derivada ordinaria
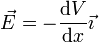
Conocido el campo, hallamos la fuerza sobre una carga puntual multiplicando por el valor de ésta
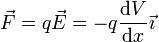
Por tanto, para hallar el sentido de la fuerza solo necesitamos el signo de la derivada, el cuál a su vez nos lo da la pendiente de la gráfica.
Para el caso de que la carga sea positiva, el sentido de la fuerza el el opuesto al signo de la pendiente. Esto nos da, para la gráfica de la figura, que es hacia la derecha para x < −3 mm y para x > +1 mm; es hacia la izquierda entre x = −2 mm y x = +1 mm. En el intervalo entre x = −3 mm y x = −2 mm, la fuerza es nula.
El módulo de la fuerza es máxima donde mayor sea la pendiente, lo cual ocurre para x < −3 mm y para x > +4 mm. Para hallar el valor numérico del módulo hallamos la pendiente a partir de la gráfica y multiplicamos por la carga, resultando la siguiente tabla:
| x < −3 mm | −3 mm < x < −2 mm | −2 mm < x < +1 mm | +1 mm < x < +4 mm | x > +4 mm | |
 (mN) (mN)
| 
| 
| 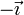
| 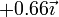
| 
|
Una partícula de carga positiva que se libera en x = 0 mm describe un movimiento oscilatorio no armónico entre x = −4 mm y x = 0 mm. Esto puede verse tanto a partir del sentido de la fuerza como de la curva de energía potencial, que para una carga positiva tiene la misma forma que la gráfica del potencial eléctrico.
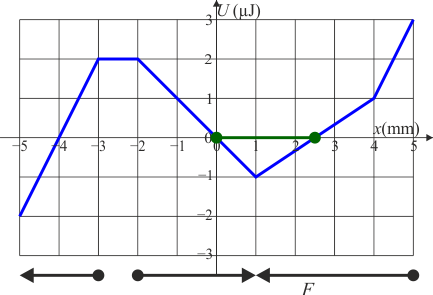
| q > 0 | q < 0 |
|---|---|
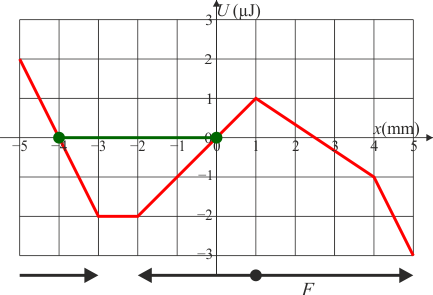
| 
|
Para una carga negativa el sentido de la fuerza es el opuesto al que acabamos de hallar (esto es, es igual al signo de la pendiente). La curva de energía potencial para una carga negativa es la opuesta en signo a la curva de potencial. Esto quiere decir que una carga negativa liberada en x = 0 mm describe un movimiento oscilatorio entre x = 0 mm y x = 2.5 mm.





