Potencial eléctrico en el eje de un anillo

De Laplace

Contenido

1 Enunciado
2 Potencial eléctrico
3 Trabajo para traer una carga positiva
4 Movimiento de una carga negativa

1 Enunciado

Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia $z$ al plano del anillo.

¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo?

Supongamos que en lugar de una carga positiva tenemos una de −2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia 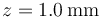$z= 1.0\,\mathrm{mm}$ del centro del anillo, ¿qué tipo de movimiento describe esta carga?

2 Potencial eléctrico

El potencial debido a una distribución de carga, como el campo eléctrico puede calcularse sumando la contribución de elementos de carga. Si suponemos el origen de potencial en el infinito,

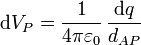
$\mathrm{d}V_P = \frac{1}{4\pi\varepsilon_0}\,\frac{\mathrm{d}q}{d_{AP}}$

siendo $V P$ el potencial en el punto P, $d q$ la carga contenida en un elemento situado en el punto A y $d A P$ la distancia entre los dos puntos.

En el caso del anillo, dividimos la circunferencia en porciones diferenciales, cada una de las cuales almacena una carga

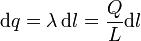
$\mathrm{d}q=\lambda\,\mathrm{d}l=\frac{Q}{L}\mathrm{d}l$

Para un punto del eje del anillo, todos los puntos de éste se encuentran a la misma distancia

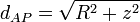
$d_{AP}=\sqrt{R^2+z^2}$

de manera que la integral que nos da el potencial en el punto P es

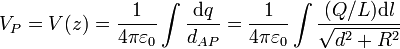
$V_P = V(z) = \frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q}{d_{AP}}=\frac{1}{4\pi\varepsilon_0}\int \frac{(Q/L)\mathrm{d}l}{\sqrt{d^2+R^2}}$

En esta integral, todos los factores son independientes del punto del anillo que tomemos, por lo que pueden extraerse de la integral y esta se reduce a

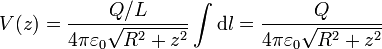
$V(z) = \frac{Q/L}{4\pi\varepsilon_0\sqrt{R^2+z^2}}\int \mathrm{d}l=\frac{Q}{4\pi\varepsilon_0\sqrt{R^2+z^2}}$

Este potencial posee un máximo en el centro del anillo y a partir de ahí decae al alejarnos de éste.

El valor del potencial en el centro del anillo es igual a

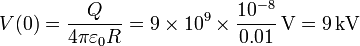
$V(0) = \frac{Q}{4\pi\varepsilon_0R}=9\times 10^9\times\frac{10^{-8}}{0.01}\,\mathrm{V}=9\,\mathrm{kV}$

Vemos no hacen falta cargas muy grandes para producir voltajes elevados.

3 Trabajo para traer una carga positiva

El trabajo para mover una carga puntual en un campo externo es igual al producto de la carga por la diferencia de potencial entre el punto inicial y el final

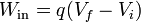
$W_\mathrm{in}=q(V_f-V_i)\,$

En este caso el punto inicial es el infinito, que hemos tomado como origen de potencial y el final es el centro del anillo, cuyo voltaje acabamos de calcular. Por tanto

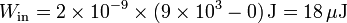
$W_\mathrm{in}= 2\times 10^{-9}\times (9\times 10^3-0)\,\mathrm{J}=18\,\mu\mathrm{J}$

4 Movimiento de una carga negativa

En el caso de que acerquemos una carga positiva al anillo, debemos realizar un trabajo positivo, ya que el anillo repele a la carga y por ello debemos vencer la fuerza eléctrica. En términos energéticos equivale a “ascender una montaña”, cuya gráfica es proporcional a la del potencial que está representada más arriba.

Si lo que se acerca es una carga negativa la situación se invierte. En ese caso el anillo atrae a la carga y lo que era una montaña se convierte en un valle. El trabajo que se realiza es negativo porque en ese caso hay que retener a la carga y extraerle la energía cinética que gana como consecuencia de la disminución de la energía potencial.

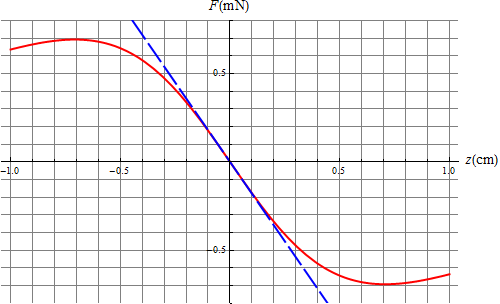
Si situamos en reposo una carga negativa en el centro del anillo, se queda en equilibrio ya que en este punto el campo eléctrico es nulo. Si ahora la separamos una cierta distancia a lo largo del eje, aparece una fuerza atractiva que tiende a devolverla a la posición original. Esto ocurre tanto si la separamos por arriba del anillo como por debajo de él. Por tanto, la fuerza eléctrica es una fuerza recuperadora en este caso y la partícula describe un movimiento oscilatorio. El movimiento no será armónico ya que la fuerza eléctrica no es simplemente lineal con la distancia (o equivalentemente, la energía potencial no tiene una gráfica parabólica). Empleando las fórmulas del campo eléctrico y el potencial a lo largo del eje obtenemos las expresiones

$\vec{F} = (-q)\vec{E}=-\frac{qQ z}{4\pi\varepsilon_0(R^2+z^2)^{3/2}}\vec{k}\qquad\qquad U(z) = (-q)V(z) = -\frac{qQ}{4\pi\varepsilon_0\sqrt{R^2+z^2}}$

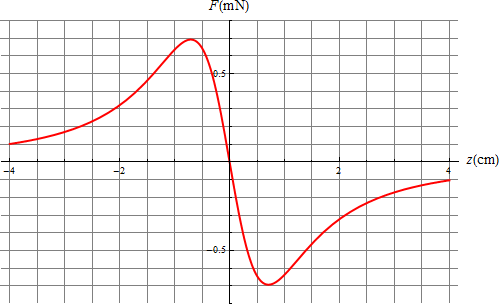
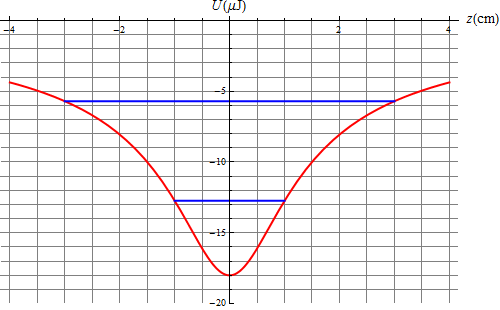
Para cada valor de la posición inicial, la carga posee una energía mecánica igual al valor de su energía potencial en ese punto y a partir de ahí describe oscilaciones, aumentando su energía cinética, que alcanza un máximo al pasar por el centro del anillo, punto a partir del cual se reduce su rapidez hasta detenerse en el punto simétrico del inicial, repitiéndose ahora el proceso en sentido opuesto.

Si la posición inicial es próxima al plano del anillo (como ocurre en el caso del enunciado, ya que se separa solo 1mm de un anillo de 1cm de radio), puede hacerse la aproximación de que z es despreciable frente a R y escribir

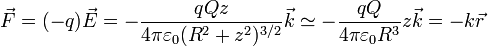
$\vec{F} = (-q)\vec{E}=-\frac{qQ z}{4\pi\varepsilon_0(R^2+z^2)^{3/2}}\vec{k}\simeq -\frac{qQ}{4\pi\varepsilon_0 R^3}z\vec{k}=-k\vec{r}$

que es la ley de Hooke para un oscilador de constante

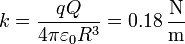
$k = \frac{qQ}{4\pi\varepsilon_0 R^3}=0.18\,\frac{\mathrm{N}}{\mathrm{m}}$

En términos de la energía, esto equivale a aproximarla por una parábola, reteniendo hasta el segundo término de la serie de Taylor

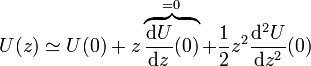
$U(z)\simeq U(0) + z \overbrace{\frac{\mathrm{d}U}{\mathrm{d}z}(0)}^{=0}+\frac{1}{2}z^2\frac{\mathrm{d}^2U}{\mathrm{d}z^2}(0)$

lo que da

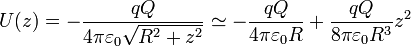
$U(z) =-\frac{qQ}{4\pi\varepsilon_0\sqrt{R^2+z^2}} \simeq -\frac{qQ}{4\pi\varepsilon_0 R}+\frac{qQ}{8\pi\varepsilon_0 R^3}z^2$

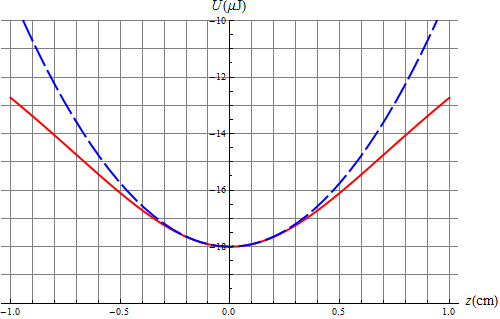
Puesto que la posición inicial es de 1mm prácticamente la carga se encuentra en el vértice de la curva, por lo que la aproximación paraólica es muy adecuada.

Hay que señalar que, aunque parece de este análisis que el centro del anillo es un punto de equilibrio estable, esto solo es así si la carga solo puede moverse a lo largo del eje. Si además se permite que se mueva lateralmente ya la posición es inestable, ya que cualquier separación lateral provoca que se vaya hacia el lado del anillo que tiene más cerca.

Potencial eléctrico en el eje de un anillo

De Laplace

Contenido

1 Enunciado

2 Potencial eléctrico

3 Trabajo para traer una carga positiva

4 Movimiento de una carga negativa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES