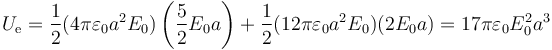Cálculos a partir de un campo eléctrico (GIE)
De Laplace
Contenido |
1 Enunciado
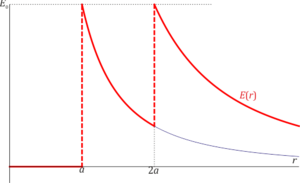
El valor de un campo eléctrico en todos los puntos del espacio viene dado por
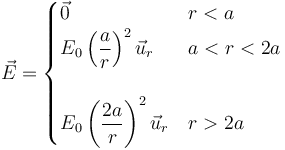
siendo r la distancia al origen de coordenadas y 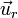 el vector unitario radial hacia afuera.
el vector unitario radial hacia afuera.
- Calcule las densidades de carga que causan este campo.
- ¿Cuánto vale la carga total de la distribución?
- Halle el potencial eléctrico en r = 0, en r = a y en r = 2a, tomando como origen de potencial el infinito.
- Calcule la energía electrostática almacenada en este sistema.
2 Densidades de carga
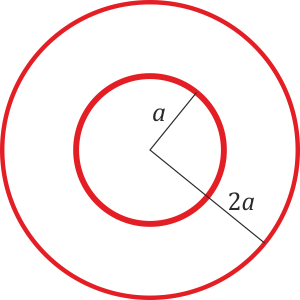
El campo presenta un salto en r = a y otro en r = 2a, lo cual indica que a esas distancias se hallan densidades superficiales de carga. Además, podría haber densidades de carga de volumen en el resto del espacio.
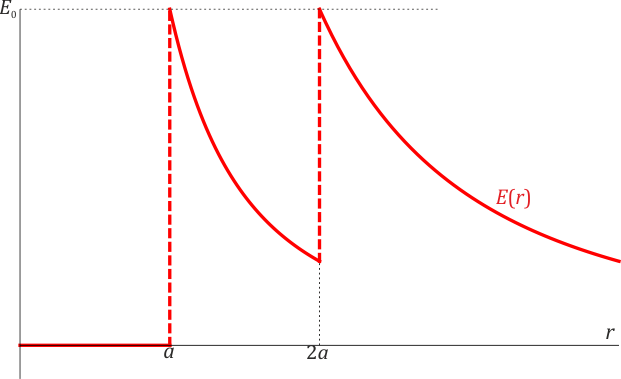
Podemos hallar las densidades calculando la carga almacenada hasta una cierta distancia del centro y viendo cómo varía. Esto lo logramos aplicando la ley de Gauss. Al tratrse de un campo radial y dependiente solo de la distancia al origen se cumple, para cualquier distancia al centro
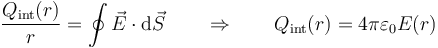
Esto nos da
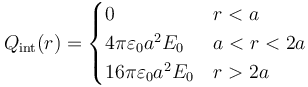
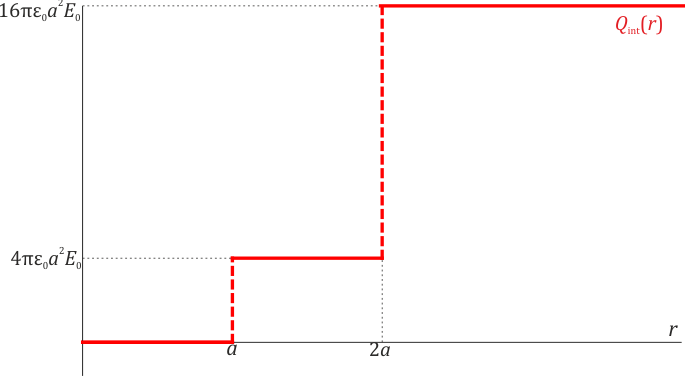
Separamos por regiones:
- En r < a, la carga encerrada es siempre 0, lo cual indica que la densidad de carga es nula en todos los puntos de esta región.
- Para a < r < 2a vemos que de entrada sí encerramos una carga, pero luego este valor permanece constante en toda la región. Esto nos dice que hay una densidad superficial de carga en r = a pero que no hay de volumen (ya que si hubiera, la carga encerrada iría cambiando con r). La densidad superficial de carga vale
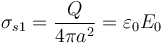
- Igualmente puede hallarse a partir de la discontinuidad del campo
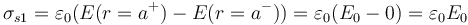
- En r = 2a tenemos un nuevo salto y a partir de ahí vuelve a salir una carga encerrada constante. Esto nos dice que de nuevo tenemos solo una densidad superficial de carga. La cantidad de carga encerrada es ahora
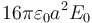 , pero esta incluye también la de r = a, por tanto, la densidad en r = 2a vale
, pero esta incluye también la de r = a, por tanto, la densidad en r = 2a vale
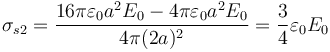
- De nuevo, puede hallarse a partir del salto del campo

- Nótese que para hallar el salto no se puede dejar el campo en función de r, sino que hay que sustituir su valor r = 2a.
Por tanto, las densidades de carga que crean el campo son
- Una superficie esférica de radio a y densidad de carga
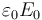 .
.
- Una superficie esférica de radio 2a y densidad de carga
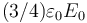 .
.
siendo nula la densidad volumétrica de carga
A este resultado se puede llegar por simple inspección observando que tenemos un campo que es nulo en una región y que en otras decae como r2, que es la conducta del campo de una carga puntual. La distribución de carga que produce un campo nulo en su interior y como el de una carga puntual es una superficie esférica cargada uniformemente.
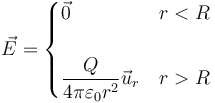
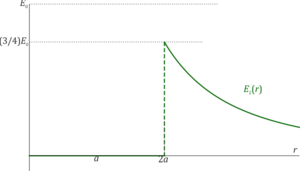
Concretamente, nuestro campo puede escribirse como
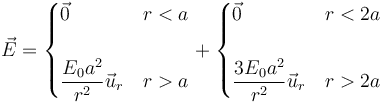
(el 3 procede de restar el 1 del primer campo al 4 del campo exterior)
Esto nos dice que tenemos dos superficies esféricas cargadas de radios a y 2a, con cargas
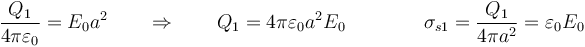
y
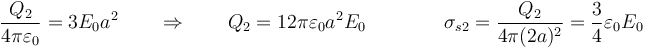

3 Carga total
No hace falta calcular la carga total integrando las densidades de carga. Es simplemente la carga encerrada por una superficie de radio r > 2a
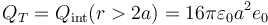
4 Potencial eléctrico
Podemos hallar el potencial eléctrico integrando el campo o a partir de las densidades de carga.
4.1 Integrando el campo
Si tomamos el origen de potencial en el infinito, el potencial a cualquier distancia del origen se calcula por la integral
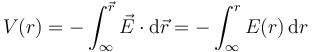
Así, nos queda:
- r = 2a
- Tenemos un solo tramo
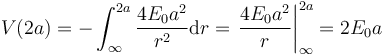
- r = a
- Tenemos dos tramos
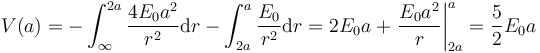
- r = 0
- Tenemos tres tramos, pero el último tiene campo nulo, por lo que
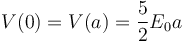
4.2 A partir de las cargas
El potencial debido a una superficie esférica cargada uniformemente es de la forma
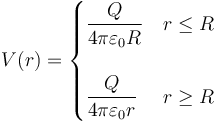
En uestro caso tenemos dos superficies esféricas, por lo que debemos aplicar superposición. Así queda
- r = 2a
- Estamos fuera de las dos esferas
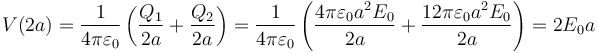
- r = a
- Estamos fuera de la esfera interior y dentro de la exterior
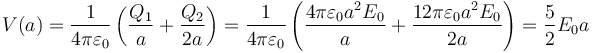
- r = 0
- Estamos dentro de las dos esferas
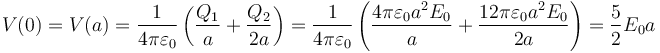
5 Energía almacenada
La energía almacenada puede calcularse a partir de la densidad de energía eléctrica, integrando en todo el espacio
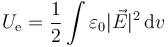
pero es más sencillo aplicando que sabemos que dos superficies eféricas cargadas concéntricas. La energía almacenada es simplemente
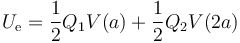
lo que da