Energía electrostática de un sistema de cargas puntuales

De Laplace

1 Enunciado

Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales:

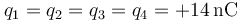$q_1=q_2=q_3=q_4=+14\,\mathrm{nC}$ .
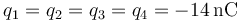$q_1=q_2=q_3=q_4=-14\,\mathrm{nC}$ .
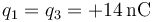$q_1=q_3=+14\,\mathrm{nC}$ , $q_2=q_4=-14\,\mathrm{nC}$ .
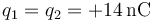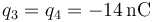$q_1=q_2=+14\,\mathrm{nC}$ , $q_3=q_4=-14\,\mathrm{nC}$ .
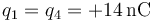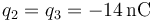$q_1=q_4=+14\,\mathrm{nC}$ , $q_2=q_3=-14\,\mathrm{nC}$ .

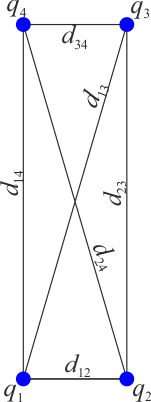
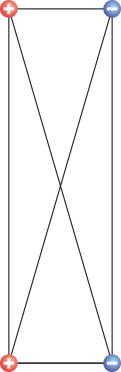
situadas en cada caso en los vértices de un rectángulo

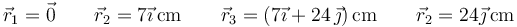
$\vec{r}_1 = \vec{0}\qquad \vec{r}_2 = 7\vec{\imath}\,\mathrm{cm}\qquad \vec{r}_3 = (7\vec{\imath}+24\,\vec{\jmath})\,\mathrm{cm}\qquad \vec{r}_2 = 24\vec{\jmath}\,\mathrm{cm}$

2 Solución

La energía de un sistema de cargas puntuales se calcula mediante la fórmula

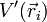$U = \frac{1}{2}\sum_i q_i V'(\vec{r}_i)$

Siendo $V'(\vec{r}_i)$ el potencial creado por el resto de las cargas en la posición de la carga i. A su vez, este potencial viene dado por la suma

$V'(\vec{r}_i)=\frac{1}{4\pi\varepsilon_0}\sum_{k\neq i}\frac{q_k}{d_{ik}}$

siendo $d i k$ la distancia entre $q i$ y $q k$ .

En este problema las posiciones son las mismas en todos los casos. Las distancias respectivas valen

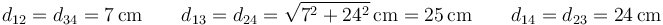
$d_{12}=d_{34}=7\,\mathrm{cm}\qquad d_{13}=d_{24}=\sqrt{7^2+24^2}\,\mathrm{cm}=25\,\mathrm{cm}\qquad d_{14}=d_{23}=24\,\mathrm{cm}$

Llevando la expresión del potencial a la de la energía queda

$\begin{array}{rcl}U & = & \displaystyle \frac{1}{8\pi\varepsilon_0}\left(q_1\left(\frac{q_2}{d_{12}}+\frac{q_3}{d_{13}}+\frac{q_4}{d_{14}}\right)+q_2\left(\frac{q_1}{d_{12}}+\frac{q_3}{d_{23}}+\frac{q_4}{d_{24}}\right)\right. +\\ && \\ & + & \displaystyle \left. q_3\left(\frac{q_1}{d_{13}}+\frac{q_2}{d_{23}}+\frac{q_4}{d_{34}}\right)+q_4\left(\frac{q_1}{d_{14}}+\frac{q_2}{d_{23}}+\frac{q_3}{d_{34}}\right)\right)\end{array}$

Agrupando términos y teniendo en cuenta que las cargas se encuentran en un rectángulo, de forma que varias de las distancias son coincidentes queda

$U = \displaystyle \frac{1}{4\pi\varepsilon_0}\left(\frac{q_1q_2+q_3q_4}{d_{12}}+\frac{q_1q_3+q_2q_4}{d_{13}}+\frac{q_1q_4+q_2q_3}{d_{14}}\right)$

Sustituimos los valores numéricos, para lo cual medimos las distancias en centímetros y las cargas en nanoculombios, quedando la energía (aproximada tomando $k_e = 9\times 10^9\,\mathrm{N}\cdot\mathrm{m}^2/\mathrm{C}^2$ ) en microjulios

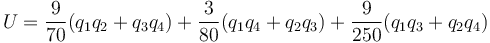
$U = \frac{9}{70}(q_1q_2+q_3q_4)+\frac{3}{80}(q_1q_4+q_2q_3)+\frac{9}{250}(q_1q_3+q_2q_4)$

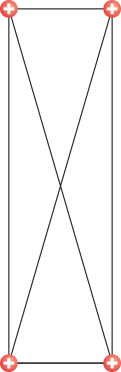
Sustituyendo ahora los diferentes valores queda la siguiente tabla:

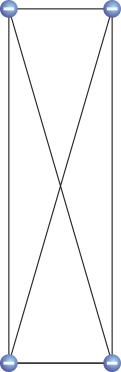
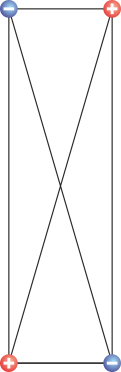
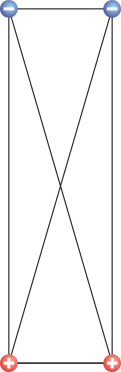
I	II	III	IV	V

Caso	$q 1$ (nC)	$q 2$ (nC)	$q 3$ (nC)	$q 4$ (nC)	$U$ (μJ)
I	+14	+14	+14	+14	+79.2
II	−14	−14	−14	−14	+79.2
III	+14	−14	+14	−14	−51.0
IV	+14	+14	−14	−14	+21.6
V	+14	−14	−14	+14	−49.8

La energía en el primer y el segundo caso son idénticas, ya que si cambiamos el signo de todas las cargas sus productos conservan el mismo signo, resultando la misma energía.

A partir de esta tabla podemos ver, por ejemplo, si partimos del tercer caso, qué trabajo costaría intercambiar la carga 2 con la carga 3. En ese caso el estado final sería el cuarto caso y el trabajo necesario la diferencia entre los dos valores de la energía.

También vemos que el que haya dos cargas positivas y dos negativas no implica en absoluto que la energía electrostática sea nula. Puede ser negativa pero también nula o positiva, dependiendo de las posiciones de las cargas.

Energía electrostática de un sistema de cargas puntuales

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES