Cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Introducción
2 Posición
3 Velocidad
4 Aceleración
- 4.1 Definición
- 4.2 Cálculo de la velocidad y posición
5 Ejemplos de movimiento rectilíneo
6 Documentación adicional
7 Problemas

1 Introducción

Antes de considerar el problema completo del movimiento de una partícula en el espacio de tres dimensiones, examinaremos el problema unidimensional, más simple, de una partícula que realiza un movimiento rectilíneo

2 Posición

Cuando tenemos una partícula cuyo movimiento se ciñe a una recta, no necesitamos el álgebra vectorial para identificar las diferentes posiciones de la partícula. Nos basta con una etiqueta $x$ que designa la posición a lo largo de la recta. Si anotamos entonces las sucesivas posiciones en instantes determinados podemos construir una tabla de posiciones frente al tiempo, por ejemplo

t (s)	0.0	0.1	0.2	0.3	0.4	0.5	0.6
x (m)	−1.728	−0.440	0.560	1.296	1.792	2.072	2.160

t (s)	0.7	0.8	0.9	1.0	1.1	1.2	1.3
x (m)	2.080	1.856	1.512	1.072	0.560	0.000	−0.584

t (s)	1.4	1.5	1.6	1.7	1.8	1.9	2.0
x (m)	−1.168	−1.728	−2.240	−2.680	−3.024	−3.248	−3.328

La posición tiene un signo que indica si nos encontramos a la izquierda o a la derecha de la posición a lo largo de la recta que hayamos etiquetado como $x = 0$ .

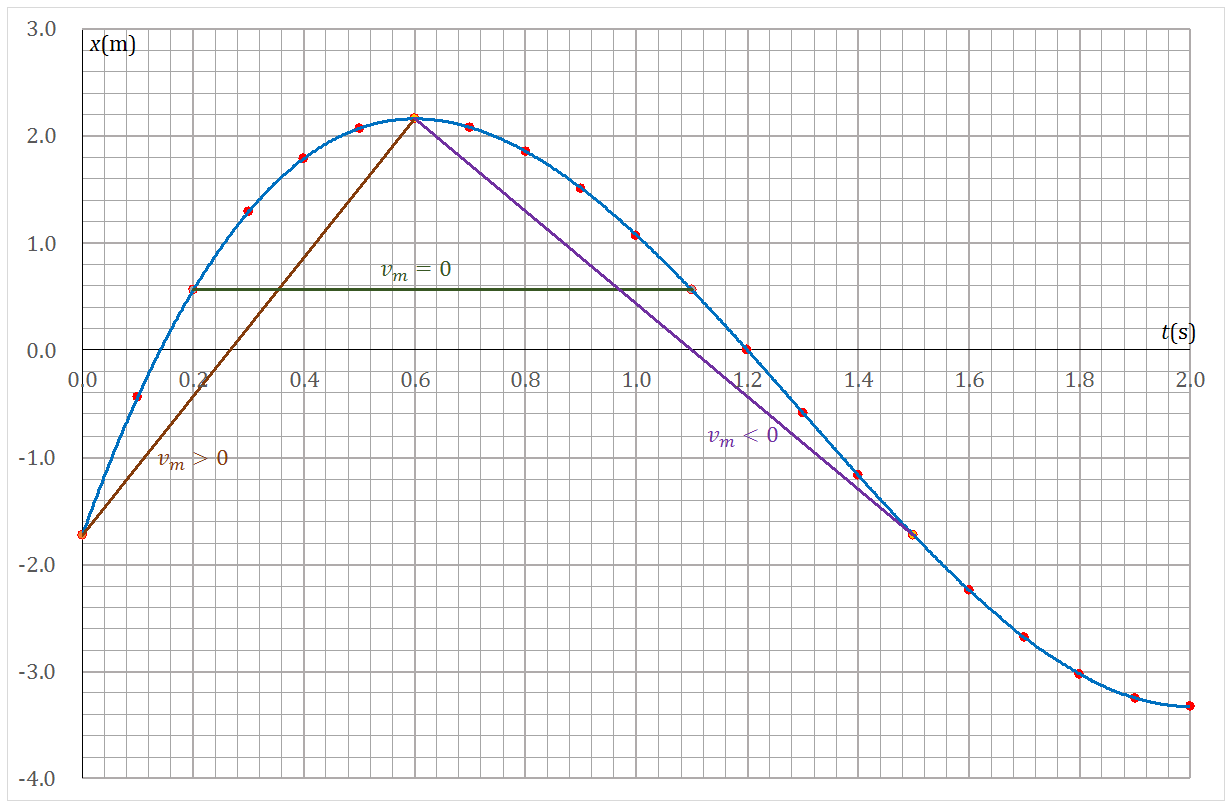
En el caso unidimensional podemos representar la posición frente al tiempo, colocando el tiempo en el eje de abscisas y la posición en el de ordenadas. Esta posibilidad no existe en el caso tridimensional. Así, para la tabla anterior, quedaría

Puesto que las partículas no se teletransportan de un sitio a otro, podemos admitir que, uniendo los puntos medidos, existe una función continua $x (t)$ que nos da la posición en cualquier instante de tiempo. Esta función puede conocerse a menudo analíticamente, dando una fórmula, pero en otras proviene de medidas experimentales, con lo que debe interpolarse a partir de los datos conocidos.

Interpolación de dos puntos

La interpolación más sencilla consiste en suponer que conocemos la posición en dos instantes. En $t 1$ la partícula se halla en $x 1$ y en $t 2$ se encuentra en $x 2$ . Para los instantes intermedios, suponemos que la partícula va pasando progresivamente de una posición a la otra, siendo la gráfica un segmento rectilíneo. En ese caso, se cumple

$x= A + Bt\,$

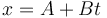
con las condiciones

$x_1=x(t_1)=A + Bt_1\qquad\qquad x_2=x(t_2)=A + Bt_2$

Resolviendo el sistema de ecuaciones para A y B queda

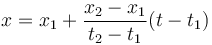
$x = x_1 + \frac{x_2-x_1}{t_2-t_1}(t-t_1)$

A este mismo resultado se llega por semejanza de triángulos

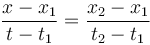
$\frac{x-x_1}{t-t_1}=\frac{x_2-x_1}{t_2-t_1}$

Cuando una partícula cambia de posición pasando de encontrarse en $x 1$ en el instante $t 1$ a una posición $x 2$ en el instante $t 2$ se dice que en el intervalo de tiempo

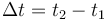
$\Delta t = t_2-t_1\,$

ha experimentado un desplazamiento

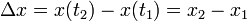
$\Delta x = x(t_2) - x(t_1) = x_2-x_1\,$

El desplazamiento que, como la posición, se mide en unidades de distancia (m, en el SI), posee la propiedad de que es independiente de que punto se toma como origen de posiciones.

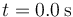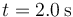Así, para el ejemplo tabulado, el desplazamiento entre $t=0.0\,\mathrm{s}$ y $t = 2.0\,\mathrm{s}$ vale

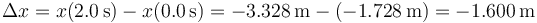
$\Delta x = x(2.0\,\mathrm{s})-x(0.0\,\mathrm{s})=-3.328\,\mathrm{m}-(-1.728\,\mathrm{m})= -1.600\,\mathrm{m}$

El desplazamiento tiene un signo que indica si nos movemos hacia las x crecientes o hacia las decrecientes.

3 Velocidad

3.1 Velocidad media

Si una partícula realiza un desplazamiento $Δ x$ en un intervalo $Δ t$ , se define la velocidad media (en una dimensión) como el cociente entre el desplazamiento y el intervalo empleado en realizarlo

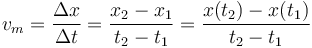
$v_m = \frac{\Delta x}{\Delta t} = \frac{x_2-x_1}{t_2-t_1}=\frac{x(t_2)-x(t_1)}{t_2-t_1}$

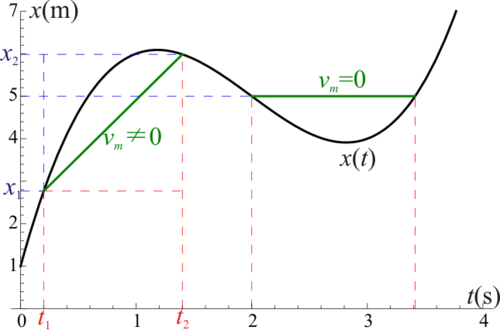
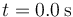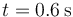Así, para la tabla anterior tendríamos que la velocidad media entre $t=0.0\,\mathrm{s}$ y $t = 0.6\,\mathrm{s}$ resulta

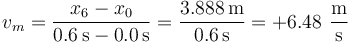
$v_m=\frac{x_6-x_0}{0.6\,\mathrm{s}-0.0\,\mathrm{s}}= \frac{3.888\,\mathrm{m}}{0.6\,\mathrm{s}}= +6.48\,\,\frac{\mathrm{m}}{\mathrm{s}}$

Entre 0.2s y 1.1s

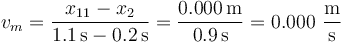
$v_m=\frac{x_{11}-x_2}{1.1\,\mathrm{s}-0.2\,\mathrm{s}}= \frac{0.000\,\mathrm{m}}{0.9\,\mathrm{s}}= 0.000\,\,\frac{\mathrm{m}}{\mathrm{s}}$

y entre 0.6s y 1.5s

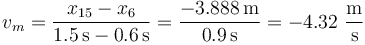
$v_m=\frac{x_{15}-x_6}{1.5\,\mathrm{s}-0.6\,\mathrm{s}}= \frac{-3.888\,\mathrm{m}}{0.9\,\mathrm{s}}= -4.32\,\,\frac{\mathrm{m}}{\mathrm{s}}$

De la definición se desprende que:

Posee unidades de distancia dividida por tiempo, que en el sistema internacional serán m/s.
La velocidad media depende del desplazamiento neto entre dos puntos, por tanto si al final del intervalo la posición es la misma que al principio, la velocidad media es 0, independientemente de las idas y vueltas que se hayan dado.
La velocidad media tiene un signo que nos indica el sentido del desplazamiento neto sobre la recta.
La velocidad no es igual a espacio partido por tiempo, sino a un desplazamiento dividido por un intervalo, esto es, lo que cuenta no es el valor absoluto de la distancia o la hora que marca el reloj, sino cuánto ha cambiado la posición y cuánto tiempo se ha empleado en realizar dicho desplazamiento.
En la gráfica de la posición frente al tiempo, la velocidad media representa la pendiente de la recta secante que pasa por los puntos $(t 1, x 1)$ y $(t 2, x 2)$ . En particular si la posición inicial y la final son la misma, resulta una recta horizontal de pendiente nula.

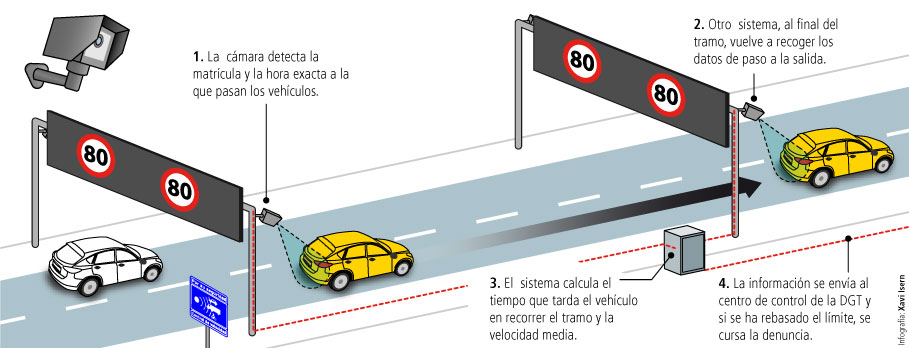
La velocidad media es lo que miden, por ejemplo, los cinemómetros de tramo de la DGT, que no son realmente radares (que es como se les conoce). Toman fotografías a la entrada y a la salida del tramo (p.ej, un túnel), leyendo la matrícula de cada vehículo y anotando el instante en que se toma la foto. La velocidad media la calculan dividiendo la longitud del túnel (conocida) por la diferencia entre las horas de las dos fotos del mismo vehículo. Si la diferencia entre estos dos instantes es demasiado pequeña, se comete una infracción.

3.2 Velocidad instantánea

El concepto de velocidad media no es especialmente útil, ya que solo nos informa del ritmo promedio, pero un movimiento concreto puede hacerse de forma irregular y normalmente interesa definir la velocidad en un momento dado, conocida como velocidad instantánea. Hoy día, con la presencia de velocímetros en los automóviles, el concepto de velocidad instantánea es intuitivo y todos tenemos una experiencia directa de la magnitud. Se trata de precisar matemáticamente el concepto.

Cuando decimos que en un instante dado la velocidad es de 120 km/h, ¿qué estamos diciendo exactamente? Evidentemente, no que durante la última hora se han recorrido 120 km, ya que igual sólo se llevan 10 minutos de marcha. Podríamos decir que durante el último minuto se han recorrido 2 km. ya que

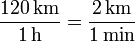
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}$

Esto ya es más preciso, pero aun no es del todo satisfactorio, ya que en un minuto hay tiempo suficiente a acelerar o frenar. Una mejor aproximación sería afirmar que en el último segundo se ha recorrido (1/30) km = 33.3 m. O podríamos decir que en la última décima de segundo se han recorrido 3.33 m,…

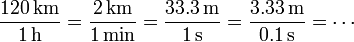
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}= \frac{33.3\,\mathrm{m}}{1\,\mathrm{s}}=\frac{3.33\,\mathrm{m}}{0.1\,\mathrm{s}}=\cdots$

En todos los casos la velocidad es de 120 km/h, pero cuanto más pequeño es el intervalo de tiempo considerado, más nos acercamos al ideal de medir la velocidad en un instante dado.

Definimos entonces la velocidad instantánea en una dimensión como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero (se reduce a un instante)

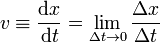
$v\equiv\frac{\mathrm{d}x}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}$

Matemáticamente, esto quiere decir que la velocidad instantánea es la derivada respecto al tiempo de la posición instantánea. En mecánica, una derivada respecto al tiempo suele representarse con un punto sobre la magnitud

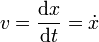
$v=\frac{\mathrm{d}x}{\mathrm{d}t} = \dot{x}$

De esta definición se deduce que:

Las unidades de la velocidad instantánea son la de una distancia dividida por un tiempo, en el SI m/s, aunque otras unidades como km/h son de uso frecuente.
La velocidad tiene un signo: es positiva si el valor de $x$ está aumentando (nos movemos hacia la derecha del punto de referencia) y es negativa si está disminuyendo (nos movemos hacia la izquierda).
La velocidad puede ser nula. En ese caso se dice que la partícula se encuentra en un estado de reposo instantáneo.
La velocidad no es igual al espacio partido por tiempo. Es la derivada de la posición respecto al tiempo.
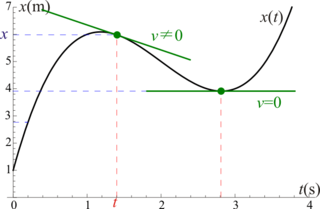
En la gráfica de la posición frente al tiempo, la velocidad representa la pendiente de la recta tangente a la curva $x (t)$ en el punto $(t, x (t))$ .
Si el estado es de reposo instantáneo esta tangente es horizontal. En ese momento usualmente la posición alcanza un máximo o un mínimo.

Siguiendo con el ejemplo numérico anterior, podemos estimar la velocidad instantánea en un momento dado (por ejemplo, t = 1.2s) a partir de un cociente entre incrementos lo más pequeños posible, tomando las diferencias con el punto tabulado inmediatamente antes o inmediatamente después. En este caso podemos tomar el intervalo (1.1s,1.2s) y el (1.2s,1.3s). En el primer caso obtenemos la aproximación

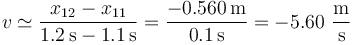
$v\simeq \frac{x_{12}-x_{11}}{1.2\,\mathrm{s}-1.1\,\mathrm{s}}= \frac{-0.560\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.60\,\,\frac{\mathrm{m}}{\mathrm{s}}$

y en el segundo

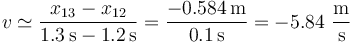
$v\simeq \frac{x_{13}-x_{12}}{1.3\,\mathrm{s}-1.2\,\mathrm{s}}= \frac{-0.584\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.84\,\,\frac{\mathrm{m}}{\mathrm{s}}$

Una mejor aproximación es la media de estos dos valores

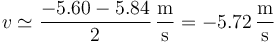
$v\simeq \frac{-5.60-5.84}{2}\,\frac{\mathrm{m}}{\mathrm{s}}= -5.72\,\frac{\mathrm{m}}{\mathrm{s}}$

Si disponemos de una expresión analítica podemos calcular la derivada de la función. Así, a la tabla de datos anterior se le puede ajustar la función cúbica

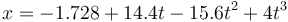
$x = -1.728+14.4t-15.6t^2+4t^3\,$

que nos vermite calcular la velocidad en cualquier instante

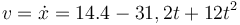
$v = \dot{x}=14.4-31,2t+12t^2\,$

que para t = 1.2s da

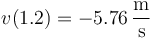
$v(1.2)=-5.76\,\frac{\mathrm{m}}{\mathrm{s}}$

Vemos que la aproximación numérica era bastante acertada. con un error de menos de un 1%.

3.3 Cálculo de la posición a partir de la velocidad

3.3.1 Velocidad como función del tiempo

Conocida la velocidad en cada instante y la posición inicial, puede hallarse la posición instantánea.

Si una partícula se mueve con velocidad variable $v (t)$ y nos preguntamos cuánto se desplaza la partícula entre $t = 0$ y $t = T$ . Evidentemente la respuesta no es igual a $v (t) T$ , ya que la velocidad es variable.

Si dividimos el intervalo de tiempo $(0, T)$ en muchos intervalos de corta duración, $Δ t$ , podemos suponer que la velocidad no varía mucho dentro de ese intervalo, y se puede suponer constante. En ese caso, el desplazamiento en el intervalo centrado en el instante $t i$ será aproximadamente

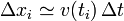
$\Delta x_i \simeq v(t_i)\,\Delta t$

y el desplazamiento total será la suma de los pequeños desplazamientos

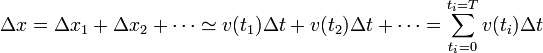
$\Delta x = \Delta x_1 + \Delta x_2 + \cdots \simeq v(t_1)\Delta t + v(t_2)\Delta t + \cdots = \sum_{t_i=0}^{t_i=T} v(t_i)\Delta t$

La aproximación será tanto mejor cuanto más pequeños sean los intervalos de tiempo, esto es, cuando se reduzcan a diferenciales. En ese caso

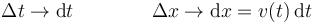
$\Delta t \to \mathrm{d}t\qquad \qquad\Delta x \to \mathrm{d}x = v(t)\,\mathrm{d}t$

Cambiando el signo de sumatorio (una S en griego) por una S alargada nos queda

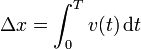
$\Delta x = \int_0^T v(t)\,\mathrm{d}t$

Considerando que T puede ser cualquier instante y no solo uno fijo, obtenemos la posición como función del tiempo, conocida la posición inicial

$\Delta x = x(t) - x_0\qquad\Rightarrow\qquad x(t) = x_0+\int_0^t v(t)\,\mathrm{d}t$

Gráficamente, este resultado se puede interpretar como el área bajo la curva $v (t)$ . Cuando consideramos intervalos $Δ t$ la cantidad $v (t i)Δ t$ es el área de un rectángulo que tiene $Δ t$ como base y $v (t i)$ como altura. El desplazamiento aproximado sería la suma de las áreas de los rectángulos, que se aproxima al área bajo la curva. La igualdad se alcanza cuando los intervalos de tiempo son diferenciales.

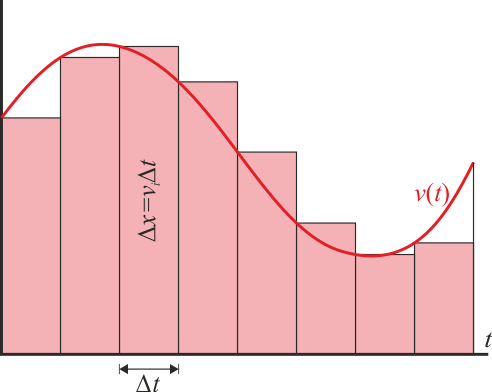
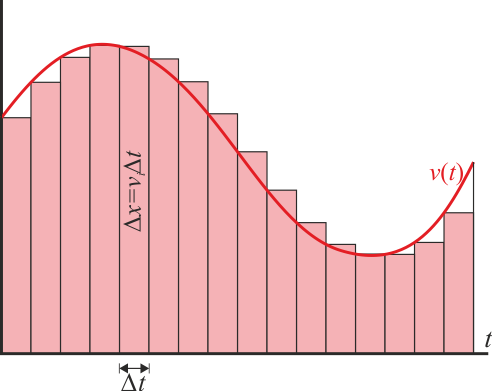
La interpretación de la integral como área bajo la curva permite obtener mejores aproximaciones al resultado a partir de los valores de la velocidad en una serie de instantes. Así tenemos el método de los trapecios, en el cual la curva se aproxima por una quebrada (lo que se llama rectificar la curva) y el área por la suma de una serie de trapecios cuya área individual es la media de las bases por la altura:

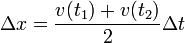
$\Delta x = \frac{v(t_1)+v(t_2)}{2}\Delta t$

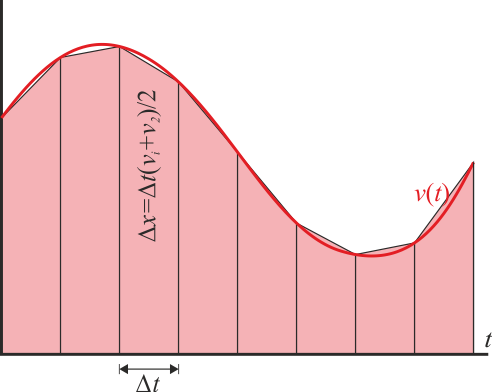
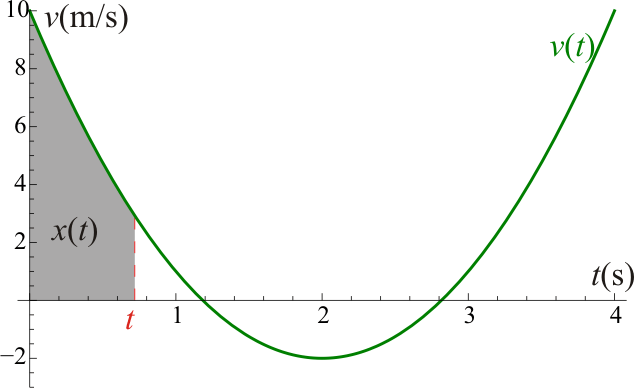
Gráficamente, si trazamos la curva de la velocidad como función del tiempo, el desplazamiento desde la posición inicial es el área bajo la curva $v = v (t)$ .

3.3.2 Velocidad como función de la posición

¿Qué ocurre si lo que conocemos es la velocidad como función de la posición? ¿Podemos también hallar la posición como función del tiempo?

Movimiento en dos tramos

Por ejemplo, supongamos que nos dicen que un coche recorre primero 120km a 120km/h y a continuación otros 120km a 60km/h. ¿Cuál es su velocidad media? NO es 90km/h, como podría pensarse ingenuamente. La razón es que el tiempo que tarda en recorrer cada tramo es diferente. Para el primer tramo emplea

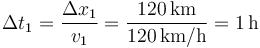
$\Delta t_1 = \frac{\Delta x_1}{v_1} = \frac{120\,\mathrm{km}}{120\,\mathrm{km}/\mathrm{h}} = 1\,\mathrm{h}$

y para el segundo

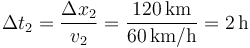
$\Delta t_2 = \frac{\Delta x_2}{v_2} = \frac{120\,\mathrm{km}}{60\,\mathrm{km}/\mathrm{h}} = 2\,\mathrm{h}$

Por tanto, el tiempo total de viaje es

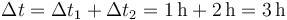
$\Delta t = \Delta t_1 + \Delta t_2 = 1\,\mathrm{h}+2\,\mathrm{h} = 3\,\mathrm{h}$

y el desplazamiento total

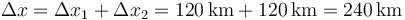
$\Delta x = \Delta x_1 + \Delta x_2 = 120\,\mathrm{km}+120\,\mathrm{km} = 240\,\mathrm{km}$

lo que nos da la velocidad media

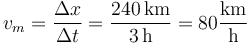
$v_m = \frac{\Delta x}{\Delta t}= \frac{240\,\mathrm{km}}{3\,\mathrm{h}} = 80\frac{\mathrm{km}}{\mathrm{h}}$ Vemos que es inferior a 90km/h (que sería la media entre las dos velocidades) porque pasa más tiempo en el tramo lento.

La idea en este caso no es hallar de entrada la posición como función del tiempo, sino calcular cuanto tiempo se tarda en llegar a un punto dado, es decir determinar $t = t (x)$ . Posteriormente se intenta invertir la relación, lo que no siempre es factible.

La expresión para el intervalo total

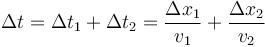
$\Delta t = \Delta t_1 + \Delta t_2 = \frac{\Delta x_1}{v_1}+\frac{\Delta x_2}{v_2}$

puede generalizarse a muchos pequeños intervalos

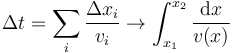
$\Delta t = \sum_i \frac{\Delta x_i}{v_i}\to \int_{x_1}^{x_2}\frac{\mathrm{d}x}{v(x)}$

El tiempo necesario para llegar a un punto dado arbitrario será la integral

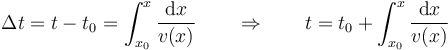
$\Delta t = t - t_0 = \int_{x_0}^x \frac{\mathrm{d}x}{v(x)}\qquad\Rightarrow\qquad t = t_0+\int_{x_0}^x\frac{\mathrm{d}x}{v(x)}$

Velocidad decreciente con x

Por ejemplo, supongamos que la velocidad disminuye linealmente con la posición

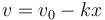
$v=v_0-kx\,$

hallándose la partícula en $x = 0$ en $t = 0$ . Separamos los diferenciales

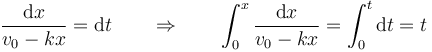
$\frac{\mathrm{d}x}{v_0-kx}=\mathrm{d}t\qquad\Rightarrow\qquad \int_0^x \frac{\mathrm{d}x}{v_0-kx} = \int_0^t \mathrm{d}t = t$

La integral del primer miembro da

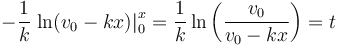
$-\frac{1}{k}\left.\ln(v_0-kx)\right|_0^x = \frac{1}{k}\ln\left(\frac{v_0}{v_0-kx}\right) = t$

De aquí sí podemos despejar x(t)

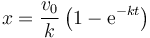
$x = \frac{v_0}{k}\left(1-\mathrm{e}^{-kt}\right)$ A este mismo resultado se puede llegar resolviendo la ecuación diferencial por otros métodos.

3.4 Rapidez

3.4.1 Definición

La velocidad instantánea posee un signo que indica el sentido de movimiento a lo largo de la recta. Sin embargo, a menudo este dato no es necesario, sino que simplemente cómo de rápido se mueve la partícula, independientemente de hacia donde. Para este caso se define la celeridad o rapidez (en inglés speed, que no es lo mismo que velocity), como el valor absoluto de la velocidad, $| v |$ . Cuando se habla de “iba a 150 km/h” se habla en realidad de la rapidez, no de la velocidad.

3.4.2 Distancia recorrida

Cuando una partícula se mueve a lo largo de una recta, el sentido de su movimiento puede ir cambiando (lo que corresponde a un cambio en el signo de la velocidad), lo cual hace que el desplazamiento neto $Δ x$ puede no coincidir con la distancia total recorrida (que denotaremos $Δ s$ ).

Desplazamiento y distancia

Por ejemplo, imaginemos un vehículo que avanza 20m y luego retrocede 5m. El desplazamiento neto será

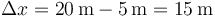
$\Delta x = 20\,\mathrm{m}-5\,\mathrm{m} = 15\,\mathrm{m}\,$

pero la distancia total recorrida es la suma de la que hace a la ida y a la vuelta

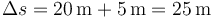
$\Delta s = 20\,\mathrm{m}+5\,\mathrm{m} = 25\,\mathrm{m}$

Analíticamente tenemos que, en cada instante de tiempo, el desplazamiento es la cantidad con signo

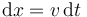
$\mathrm{d}x = v\,\mathrm{d}t$

mientras que la distancia recorrida no tiene en cuenta el signo, esto es, emplea la rapidez

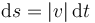
$\mathrm{d}s = |v|\,\mathrm{d}t$

El desplazamiento neto y la distancia total recorrida serán las sumas de estos diferenciales

$\Delta x = \int_0^t v\,\mathrm{d}t\qquad\qquad \Delta s = \int_0^t|v|\mathrm{d}t$

Gráficamente, el desplazamiento neto es la suma de las áreas bajo la curva, contando como negativas las que están bajo el eje. La distancia recorrida cuenta todas las áreas como positivas, esto es, es la integral del valor absoluto de la velocidad

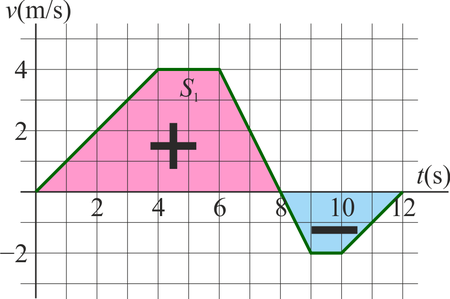
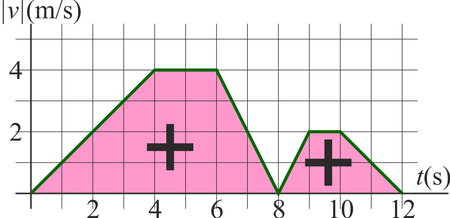
3.4.3 Celeridad media

Cuando decimos que un vehículo hizo un trayecto con una “velocidad media” de 150km/h, el sentido del movimiento no se considera, ni el que el vehículo haya podido ir y volver, por lo que con precisión se debería hablar de rapidez media o celeridad media. La definición precisa de rapidez media es análoga a la de velocidad media

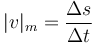
$|v|_m = \frac{\Delta s}{\Delta t}$

Si lo que conocemos es la velocidad como función del tiempo

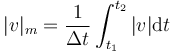
$|v|_m = \frac{1}{\Delta t}\int_{t_1}^{t_2}|v|\mathrm{d}t$

Hay que señalar que la rapidez media no es igual al módulo de la velocidad media. Por ejemplo, una partícula que recorre una distancia $L$ y luego retorna a la posición inicial, tiene una velocidad media nula, pero una rapidez media distinta de cero.

3.5 Unidades

La velocidad posee unidades de una distancia dividida por un tiempo. La unidad SI es el m/s, aunque otras unidades son de uso frecuente:

	m/s	km/h	mph	nudos
1 m/s =	1	3.600	2.2369	1.9438
1 km/h =	0.2778	1	0.6214	0.5400
1 mph =	0.4470	1.6093	1	0.8690
1 nudo =	0.5144	1.8520	1.1508	1

Una rapidez de uso frecuente en Física es la velocidad de la luz

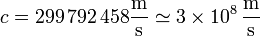
$c = 299\,792\,458 \frac{\mathrm{m}}{\mathrm{s}} \simeq 3\times 10^8\,\frac{\mathrm{m}}{\mathrm{s}}$

de forma que la velocidad de una partícula elemental suele expresarse como, por ejemplo, $v = 0.01 c$ , con lo que la velocidad de la luz funciona también como unidad de medida de velocidades.

4 Aceleración

4.1 Definición

La aceleración de un movimiento rectilíneo se define como la derivada de la velocidad instantánea, y por tanto, como la segunda derivada de la posición

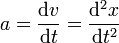
$a = \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}^2x}{\mathrm{d}t^2}$

Usando la notación de puntos para indicar la derivada respecto al tiempo

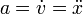
$a = \dot{v}=\ddot{x}$

De la definición se tiene que

La aceleración tiene dimensiones de longitud dividida por tiempo al cuadrado, siendo su unidad en el SI el m/s²
Una magnitud con dimensiones de aceleración que es especialmente importante es la aceleración de la gravedad en la superficie terrestre, cuyo valor estándar es, por definición,

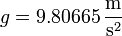
$g = 9.80665\,\frac{\mathrm{m}}{\mathrm{s}^2}$

de manera que muchas aceleraciones se expresan como múltiplos de esta unidad, aunque dichas aceleraciones no estén relacionadas con la gravedad. Así, por ejemplo, para medir las aceleraciones laterales de un piloto de Fórmula 1 en una curva se dice, por ejemplo, “está sometido a 3 fuerzas G”, que quiere decir que

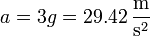
$a = 3g = 29.42\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Por tanto, g aquí funciona como unidad de medida de la aceleración.

En la gráfica $x (t)$ , la aceleración está asociada a la concavidad de la curva. Donde la aceleración es positiva la gráfica es cóncava hacia arriba, y donde es negativa es cóncava hacia abajo.

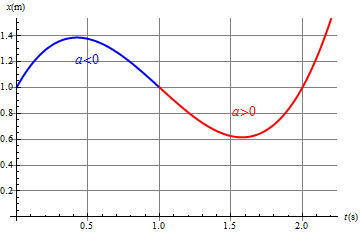
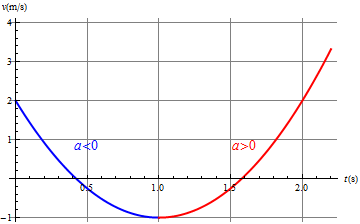
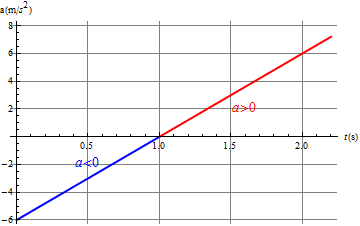
En la gráfica de la velocidad frente al tiempo, la aceleración es la pendiente de la curva, siendo positiva donde la velocidad crece y negativa donde decrece.
En el habla cotidiana se distinguen dos tipos de aceleración, diciendo que un vehículo acelera o frena según su rapidez esté aumentando o disminuyendo. 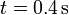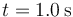Sin embargo, dado que la rapidez no es lo mismo que la velocidad (es el valor absoluto de ésta), un móvil que frena no siempre tiene una aceleración negativa y viceversa (depende de para donde se esté moviendo; así por ejemplo, en la gráfica anterior, entre $t=0.4\,\mathrm{s}$ y $t=1.0\,\mathrm{s}$ la aceleración es negativa y sin embargo la rapidez está aumentando). Por ello, conveniente emplear simplemente el término "aceleración" para todo, y dejar que el signo vaya incluido en el propio valor de la magnitud.

Al estudiar numerosos movimientos, como el de un automóvil a lo largo de una carretera, no se suele conocer la velocidad como función del tiempo, sino como función de la posición. Se sabe qué velocidad se tenía en un determinado punto (una entrada a una ciudad, un radar de la Guardia Civil,...) pero no la hora a la que esto ocurre. ¿Cómo se calcula en ese caso la aceleración? Lo hacemos empleando la regla de la cadena.

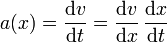
$a(x)= \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t}$

pero la derivada de la posición respecto al tiempo es la propia velocidad, por lo que

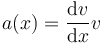
$a(x) = \frac{\mathrm{d}v}{\mathrm{d}x}v$

Usando de nuevo la regla de la cadena nos queda

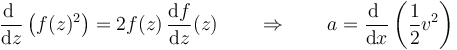
$\frac{\mathrm{d}\ }{\mathrm{d}z}\left(f(z)^2\right) = 2f(z)\,\frac{\mathrm{d}f}{\mathrm{d}z}(z)\qquad\Rightarrow\qquad a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)$

esto es, hallamos el cuadrado de la velocidad y lo dividimos por dos. La derivada de esta cantidad respecto a la posición es también la aceleración, obtenida como función de la posición.

4.2 Cálculo de la velocidad y posición

Conocida la aceleración en cada instante y la velocidad inicial, se puede hallar la velocidad en cada instante por integración de la aceleración

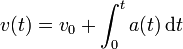
$v(t) = v_0 + \int_0^t a(t)\,\mathrm{d}t$

y la posición mediante la segunda integración

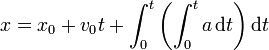
$x= x_0 + v_0 t + \int_0^t\left(\int_0^t a\,\mathrm{d}t\right)\mathrm{d}t$

5 Ejemplos de movimiento rectilíneo

Dentro de los movimientos rectilíneos existen infinitos casos posibles, ya que cualquier función continua puede representar el movimiento de una partícula.

Existen, no obstante, algunos casos particulares de interés