Ejemplo de integración numérica
De Laplace
1 Enunciado
Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica
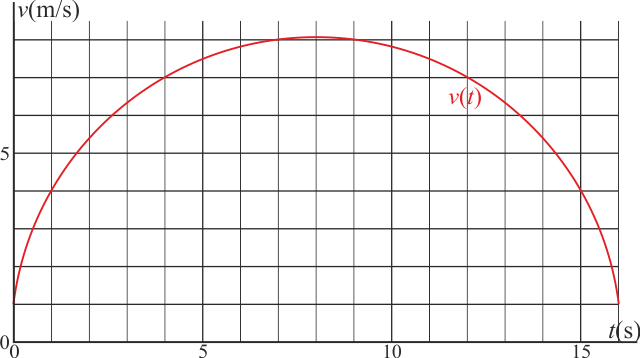
La partícula parte de s = 0.
- Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en
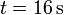 .
.
- Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es

- ¿Cuál es el error relativo cometido en el apartado anterior?
2 Solución numérica
Si conocemos la velocidad instantánea, podemos hallar el desplazamiento a base de sumar los desplazamientos diferenciales
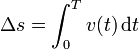
Gráficamente, esto equivale a hallar el área bajo la curva de la velocidad frente al tiempo.
Examinando la figura, podemos ver que la curva corta la cuadrícula en los puntos de coordenadas enteras (en el SI) (0,1), (1,4), (4,7), (7,8), (9,8), (12,7), (15,4) y (16,1):
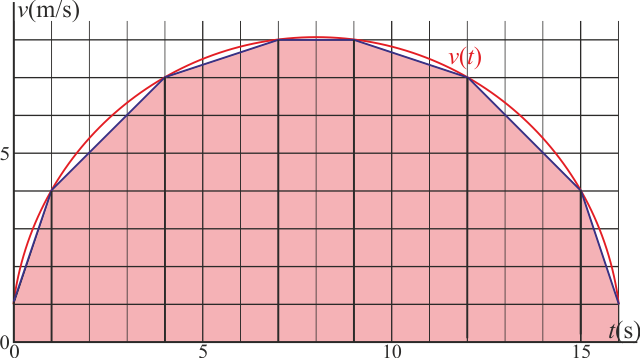
El área bajo la curva puede entonces ser aproximada por una suma de trapecios, siendo la fórmula para el área de cada uno
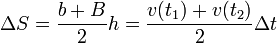
Aplicando esto a nuestro caso obtenemos el desplazamiento aproximado
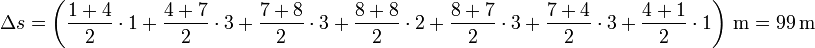
Existen otras formas numéricas de aproximar el resultado, según como se aproxime la curva. En este caso, se puede hacer coincidir con muy buena aproximación por media circunferencia de radio 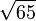 , con lo que el área valdría
, con lo que el área valdría
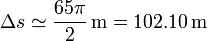
3 Solución analítica
Integrando analíticamente la función obtenemos, midiendo todas las magnitudes en el SI
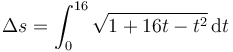
Para resolver esta integral, primero completamos cuadrados, sumando y restando 64
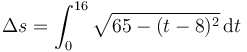
Haciendo un cambio de variable
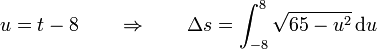
Con un nuevo cambio de variable
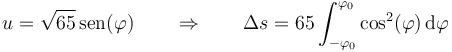
siendo
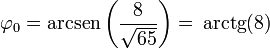
La integral trigonométrica se calcula de forma sencilla
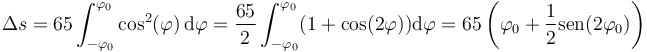
Sustituyendo el valor de 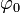
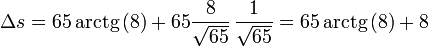
El valor numérico de este resultado es
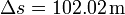
siendo el error relativo cometido
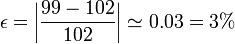
esto es un error de solo un 3%, siendo los cálculos numéricos mucho más fáciles que los exactos.
En el caso de la aproximación por medio círculo, el error es mucho menor
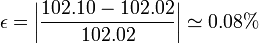
esto es, un error en la cuarta cifra decimal.





