Integración aproximada de la velocidad

De Laplace

Contenido

1 Enunciado
2 Integración numérica
3 Integración analítica
4 Error relativo
5 Aceleración numérica
6 Aceleración analítica

1 Enunciado

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

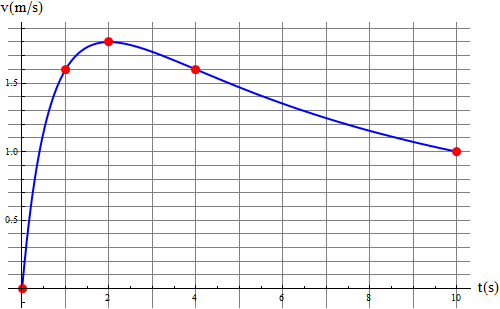
La partícula parte de $x = 0$ .

Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en $t=10\,\mathrm{s}$ .
Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad, en el SI, es

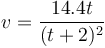
$v = \frac{14.4t}{(t+2)^2}$

¿Cuál es el error relativo cometido en el apartado anterior?

Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en 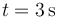$t = 3\,\mathrm{s}$ . Calcule el valor exacto y el error cometido con la aproximación.

2 Integración numérica

El área bajo la curva se puede aproximar mediante el método de los trapecios. Para ello, a partir de una serie de puntos conocidos de la curva, trazamos los trapecios que definen con el eje.

Si la curra pasa por los puntos $(t n, v n)$ y $(t n + 1, v n + 1)$ , el área de cada trapecio es la altura multiplicada por la media entre las dos bases. Este área equivale, aproximadamente, al desplazamiento entre esos dos instantes

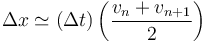
$\Delta x \simeq (\Delta t)\left(\frac{v_n+v_{n+1}}{2}\right)$

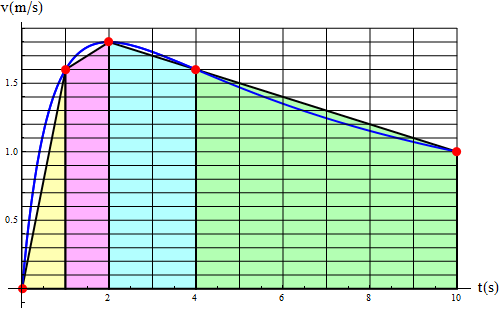
Aplicando esto a nuestro caso, tenemos los puntos señalados

t(s)	0	1	2	4	10
v (m/s)	0.0	1.6	1.8	1.6	1.0

lo que nos da el desplazamiento total

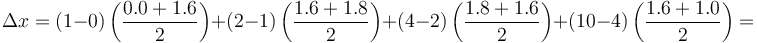
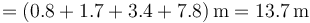
$\Delta x = (1-0)\left(\frac{0.0+1.6}{2}\right)+(2-1)\left(\frac{1.6+1.8}{2}\right)+(4-2)\left(\frac{1.8+1.6}{2}\right)+(10-4)\left(\frac{1.6+1.0}{2}\right)=$ $=(0.8+1.7+3.4+7.8)\,\mathrm{m}=13.7\,\mathrm{m}$

3 Integración analítica

Si conocemos la dependencia funcional de la velocidad con el tiempo

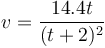
$v = \frac{14.4t}{(t+2)^2}$

podemos hallar el desplazamiento mediante su integral analítica

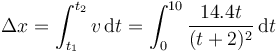
$\Delta x = \int_{t_1}^{t_2}v\,\mathrm{d}t=\int_0^{10} \frac{14.4t}{(t+2)^2}\,\mathrm{d}t$

Para hallar el valor de esta integral hacemos el cambio de variable

$u = t + 2\qquad\qquad \mathrm{d}u=\mathrm{d}t\qquad\qquad u\in[2,12]$

que convierte la integral en

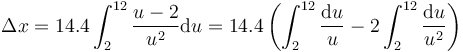
$\Delta x = 14.4\int_2^{12}\frac{u-2}{u^2}\mathrm{d}u=14.4\left(\int_2^{12}\frac{\mathrm{d}u}{u}-2\int_2^{12}\frac{\mathrm{d}u}{u^2}\right)$

El resultado final es

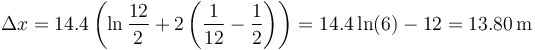
$\Delta x = 14.4\left(\ln\frac{12}{2}+2\left(\frac{1}{12}-\frac{1}{2}\right)\right)=14.4\ln(6) -12=13.80\,\mathrm{m}$

4 Error relativo

El error relativo de una magnitud es la diferencia entre lo que se mide y lo que se debería medir, comparado con lo que se debería medir

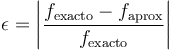
$\epsilon = \left|\frac{f_\mathrm{exacto}-f_\mathrm{aprox}}{f_\mathrm{exacto}}\right|$

En nuestro caso, el error cometido es

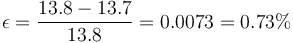
$\epsilon=\frac{13.8-13.7}{13.8} = 0.0073 = 0.73\%$

Es decir, el método numérico aproximado es mucho más simple de calcular y produce un resultado que tiene menos de un 1% de error.

5 Aceleración numérica

La derivada la podemos calcular aproximadamente a partir del cociente entre incrementos. En este caso deseamos hallar la aceleración en el punto medio entre t = 2s y t = 4s. Esta aceleración es aproximadamente

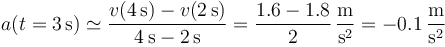
$a(t=3\,\mathrm{s})\simeq \frac{v(4\,\mathrm{s})-v(2\,\mathrm{s})}{4\,\mathrm{s}-2\,\mathrm{s}}=\frac{1.6-1.8}{2}\,\frac{\mathrm{m}}{\mathrm{s}^2}=-0.1\,\frac{\mathrm{m}}{\mathrm{s}^2}$

6 Aceleración analítica

El valor de la aceleración a partir de la expresión de la velocidad puede hallarse derivando esta

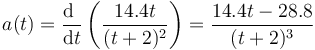
$a(t) = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{14.4t}{(t+2)^2}\right) = \frac{14.4t-28.8}{(t+2)^3}$

que en t=3 s vale

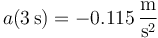
$a(3\,\mathrm{s}) = -0.115\,\frac{\mathrm{m}}{\mathrm{s}^2}$

En este caso, el error de la aproximación numérica es mayor que antes

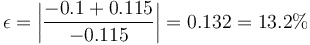
$\epsilon=\left|\frac{-0.1+0.115}{-0.115}\right| = 0.132 = 13.2\%$

Aun así, el cálculo numérico vuelve a ser mucho más sencillo que el analítico y proporciona un resultado aceptable.

Integración aproximada de la velocidad

De Laplace

Contenido

1 Enunciado

2 Integración numérica

3 Integración analítica

4 Error relativo

5 Aceleración numérica

6 Aceleración analítica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES