Frenado de un fórmula 1

De Laplace

Contenido

1 Enunciado
2 Aceleración en el SI
3 “Fuerzas G”
4 Velocidad como función de la posición
5 Caso de parada

1 Enunciado

Cuando el Ferrari de Sebastian Vettel se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 288 km/h. Cuando entra en la chicane va a 72 km/h.

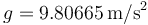Suponiendo que la aceleración es constante, determine su valor. Exprese el resultado en el SI y como un múltiplo de $g$ (siendo $g=9.80665\,\mathrm{m}/\mathrm{s}^2$ ).
Determine la velocidad como función de la posición y represéntela gráficamente.
Si el McLaren de Fernando Alonso va a 180 km/h a 150m de la chicane y se detiene a 50m de ésta, ¿es su aceleración mayor o menor que la de Vettel, en valor absoluto?

2 Aceleración en el SI

Pasamos en primer lugar los valores de la velocidad al SI. A 150m de la chicane tiene una velocidad de

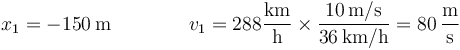
$x_1 = -150\,\mathrm{m}\qquad\qquad v_1 = 288\frac{\mathrm{km}}{\mathrm{h}}\times \frac{10\,\mathrm{m}/\mathrm{s}}{36\,\mathrm{km}/\mathrm{h}} = 80\,\frac{\mathrm{m}}{\mathrm{s}}$

y al entrar en la chicane

$x_2 = 0\,\mathrm{m}\qquad\qquad v_2 = 72\frac{\mathrm{km}}{\mathrm{h}}\times \frac{10\,\mathrm{m}/\mathrm{s}}{36\,\mathrm{km}/\mathrm{h}} = 20\,\frac{\mathrm{m}}{\mathrm{s}}$

Para hallar la aceleración aplicamos que en un movimiento uniformemente acelerado

$a = \frac{v_2^2 - v_1^2}{2(x_2-x_1)}$

Sustituyendo los valores numéricos nos queda

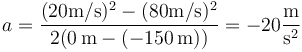
$a = \frac{(20\mathrm{m}/\mathrm{s})^2-(80\mathrm{m}/\mathrm{s})^2}{2(0\,\mathrm{m}-(-150\,\mathrm{m}))} = -20\frac{\mathrm{m}}{\mathrm{s}^2}$

3 “Fuerzas G”

En el mundo de la Fórmula 1 y otras actividades que implican grandes aceleraciones (por ejemplo, el pilotaje de un caza) se habla de que el piloto está sometido a “Fuerzas G”.

En realidad, no se está hablando de fuerzas sino de aceleraciones. Consiste en expresar la aceleración empleando como unidad la aceleración de la gravedad, cuyo valor estándar es de 9.80665 m/s². De esta forma, si un piloto experimenta “3 fuerzas G”, quiere decir que a = 3g.

El nombre de fuerzas G viene de la analogía con el peso. Por el principio de equivalencia, un cuerpo que experimenta una aceleración igual a la de la gravedad está sometido a una fuerza igual a su propio peso. Si es de 3g equivale a que el cuerpo soporta una fuerza comparable a la opresión que tendría si tuviera que aguantar a tres personas de su mismo peso, colocadas encima suya. Es fácil ver que fuerzas G superiores a 5 no se pueden soportar por periodos prolongados de tiempo.

En el caso del piloto de Fórmula 1, el valor sería

$\frac{|a|}{g} = \frac{20}{9.80665} = 2.04$

El piloto experimenta entonces 2.04 fuerzas G. El efecto físico al frenar sería equivalente a un empujón hacia adelante de más del doble del peso del piloto.

4 Velocidad como función de la posición

En el frenado de un vehículo, su velocidad va disminuyendo con la posición. Al ser la aceleración constante, podríamos pensar que la velocidad varía linealmente con la posición, pero no es así.

Si en la formula anterior

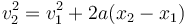
$v_2^2 = v_1^2 + 2a(x_2-x_1)$

consideramos que el instante 1 es el inicial y el 2 no es el final, sino cualquier punto intermedio, nos queda

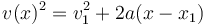
$v(x)^2 = v_1^2 + 2a(x-x_1)$

y hallando la raíz cuadrada

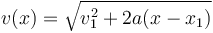
$v(x) = \sqrt{v_1^2 + 2a(x-x_1)}$

Sustituyendo los valores numéricos

$v(x) = \sqrt{400-40x}\frac{\mathrm{m}}{\mathrm{s}}$

Gráficamente, la velocidad como función de la posición experimenta una cierta curvatura (pese a que la aceleración, que es la derivada respecto al tiempo, es constante)

5 Caso de parada

En el segundo caso tenemos los valores

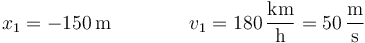
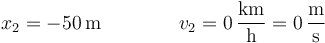
$x_1=-150\,\mathrm{m}\qquad\qquad v_1=180\,\frac{\mathrm{km}}{\mathrm{h}}=50\,\frac{\mathrm{m}}{\mathrm{s}}$ $x_2=-50\,\mathrm{m}\qquad\qquad v_2=0\,\frac{\mathrm{km}}{\mathrm{h}}=0\,\frac{\mathrm{m}}{\mathrm{s}}$

lo que nos da la aceleración

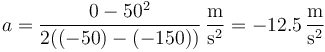
$a=\frac{0-50^2}{2((-50)-(-150))}\,\frac{\mathrm{m}}{\mathrm{s}^2}=-12.5\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Vemos que en este caso la aceleración es muy inferior.

Frenado de un fórmula 1

De Laplace

Contenido

1 Enunciado

2 Aceleración en el SI

3 “Fuerzas G”

4 Velocidad como función de la posición

5 Caso de parada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES