Movimiento sinusoidal cuadrático

De Laplace

1 Enunciado

Una partícula oscila según la ley

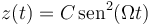
$z(t) = C\,\mathrm{sen}^2(\Omega t)$

Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

2 Solución

Para ver que se trata de un movimiento armónico podemos analizar la propia solución o comprobar si verifica la ecuación del oscilador armónico.

Hay que destacar que el hecho de que se trate de una función oscilante o periódica no equivale a que sea un movimiento armónico. Por ejemplo, si el exponente fuera un cubo en vez de un cuadrado, no se trataría de un m.a.s. Para que sea armónico debe verificarse la ecuación de movimiento

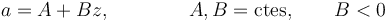
$a=A+B z,\qquad\qquad A,B=\mathrm{ctes}, \qquad B< 0$

o

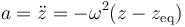
$a = \ddot{z}=-\omega^2(z-z_\mathrm{eq})$

Derivamos entonces nuestra función, para ver si se cumple una ecuación de este tipo. Primero hallamos la velocidad

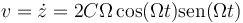
$v = \dot{z} = 2C\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)$

y derivando de nuevo la aceleración

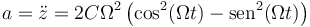
$a = \ddot{z} = 2C\Omega^2\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right)$

Aplicando la relación

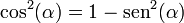
$\cos^2(\alpha) = 1 - \mathrm{sen}^2(\alpha)\,$

nos queda

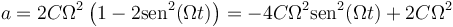
$a = 2C\Omega^2\left(1-2\mathrm{sen}^2(\Omega t)\right) = -4C\Omega^2\mathrm{sen}^2(\Omega t)+2C\Omega^2$

En el primer sumando reconocemos a la propia elongación

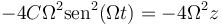
$-4C\Omega^2\mathrm{sen}^2(\Omega t)=-4\Omega^2z\,$

con lo cual la aceleración es de la forma

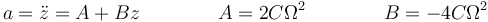
$a=\ddot{z}=A+Bz \qquad\qquad A = 2C\Omega^2\qquad\qquad B = -4C\Omega^2$

que es la ecuación general del oscilador armónico. Podemos afinar más el cálculo y hallar la posición de equilibrio, la frecuencia, amplitud y resto de parámetros.

Interesa extraer el factor $- 4Ω 2$ y escribir la aceleración como

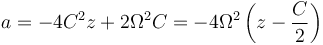
$a = -4C^2 z+ 2\Omega^2C = -4\Omega^2\left(z-\frac{C}{2}\right)$

Esta también es la ecuación de un oscilador armónico, si hacemos

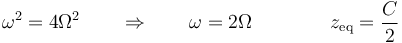
$\omega^2 = 4\Omega^2 \qquad\Rightarrow\qquad \omega = 2\Omega\qquad\qquad z_\mathrm{eq} = \frac{C}{2}$

La amplitud de las oscilaciones es la mitad de la distancia entre el valor máximo y el mínimo de la posición, que corresponden respectivamente a que el seno valga +1 (o -1) y a que valga 0.

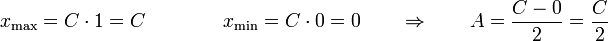
$x_\mathrm{max}=C\cdot 1 = C\qquad\qquad x_\mathrm{min} = C\cdot 0 = 0\qquad\Rightarrow\qquad A = \frac{C-0}{2}=\frac{C}{2}$

Por tanto tenemos un oscilador armónico tal que

Su punto de equilibrio se encuentra en

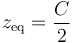
$z_\mathrm{eq} = \frac{C}{2}$

Su frecuencia angular de oscilación es igual a

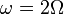
$\omega = 2\Omega\,$

Su frecuencia natural vale

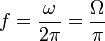
$f = \frac{\omega}{2\pi}=\frac{\Omega}{\pi}$

Su periodo de oscilación es

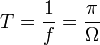
$T = \frac{1}{f}=\frac{\pi}{\Omega}$

Su amplitud vale

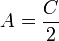
$A = \frac{C}{2}$

Podemos ver claramente estos resultados sin más que representar la función. Si el seno

lo elevamos al cuadrado queda

Al elevar el seno al cuadrado resulta una función siempre positiva, que por tanto oscila alrededor de un valor que será también positivo. Asimismo, la amplitud se reduce a la mitad mientras que la frecuencia resultante se duplica.

A este resultado se puede llegar también simplemente observando que

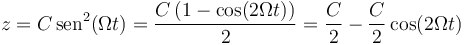
$z = C\,\mathrm{sen}^2(\Omega t) = \frac{C\left(1-\cos(2\Omega t)\right)}{2} = \frac{C}{2}-\frac{C}{2}\cos(2\Omega t)$

que es claramente una oscilación armónica de frecuencia $2Ω$ con amplitud $C / 2$ alrededor de $z eq = C / 2$ .

Por comparación, podemos ver que el cubo del seno no es una oscilación armónica

Movimiento sinusoidal cuadrático

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES