Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Problemas de boletín

1.1 Posición dependiente del tiempo

Una partícula se mueve de manera que su posición como función del tiempo está representada en la gráfica de la figura

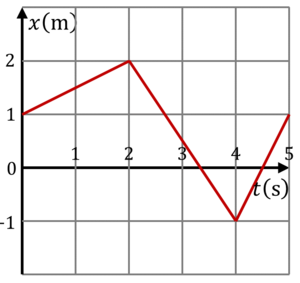
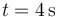  1. ¿Cuánto vale su desplazamiento entre t=0 \,\mathrm{s} y t=4 \,\mathrm{s} ?
  2. ¿Cuánto vale la distancia total recorrida en el mismo intervalo?
  3. ¿Cuánto vale el desplazamiento y la distancia total recorrida en el intervalo (0 s,5 s)?
  4. ¿Cuánto vale la velocidad media en los intervalos (0 s,5 s), (0 s,4 s) y (2 s,5 s)?
  5. ¿Cómo es la gráfica de la velocidad instantánea como función del tiempo?

1.2 Rapidez de impacto

Una partícula está sometida exclusivamente a la acción de la gravedad. Si se lanza con velocidad + v0 en dirección vertical hacia arriba desde un punto de altura h. ¿Cuál es su velocidad cuando llega al suelo? Si en vez de lanzarse hacia arriba se lanza hacia abajo, con velocidad − v0, ¿llegará con una rapidez mayor?

1.3 Persecución policial

Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?

Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?

1.4 Análisis numérico de movimiento

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6
x (m) −1.728 −0.440 0.560 1.296 1.792 2.072 2.160


t (s) 0.7 0.8 0.9 1.0 1.1 1.2 1.3
x (m) 2.080 1.856 1.512 1.072 0.560 0.000 −0.584


t (s) 1.4 1.5 1.6 1.7 1.8 1.9 2.0
x (m) −1.168 −1.728 −2.240 −2.680 −3.024 −3.248 −3.328

Para este movimiento, halle:

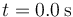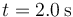  1. El desplazamiento entre t = 0.0\,\mathrm{s} y t=2.0\,\mathrm{s}, así como el valor aproximado de la distancia recorrida en dicho intervalo.
  2. La velocidad media y la rapidez media en el intervalo anterior.
  3. La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
  4. El valor aproximado de la velocidad en t= 1.2\,\mathrm{s}.
  5. El valor aproximado de la aceleración en t= 1.2\,\mathrm{s}.
  6. Sabiendo que este movimiento sigue una ley de la forma
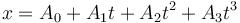
x = A_0 + A_1 t + A_2 t^2 + A_3 t^3\,
Calcule
  1. Los valores de las constantes Ak.
  2. El valor exacto de la distancia recorrida y la rapidez media.
  3. El valor exacto de la velocidad y de la aceleración en t = 1.2\,\mathrm{s}.

1.5 Calculo de magnitudes a partir de v(t)

Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI

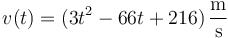
v(t) = (3t^2-66t+216)\,\frac{\mathrm{m}}{\mathrm{s}}

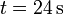entre t=0\,\mathrm{s} y t=24\,\mathrm{s}. La posición inicial es x(0) = 0\,\mathrm{m}. Halle:

  1. La posición de la partícula en cada instante del intervalo indicado.
  2. La velocidad media de la partícula en este intervalo.
  3. Los valores máximo y mínimo de x.
  4. La distancia recorrida en ese intervalo y la rapidez media.
  5. Los valores máximo y mínimo de la velocidad y la rapidez.
  6. La aceleración en todo instante.

1.6 Ejemplos de velocidad en función de la posición

1) La velocidad de una partícula sigue la ley

v = \sqrt{Ax}

siendo x la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2) Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

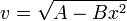
v = \sqrt{A- B x^2}

con A y B constantes positivas.

  1. ¿En que se medirá B en el SI?
  2. ¿Cómo depende de la posición la aceleración de la partícula?

1.7 Velocidad decreciente con la posición

Mediante una serie de sensores se mide la velocidad de un vehículo en puntos equiespaciados, obteniéndose la tabla

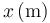
x\,(\mathrm{m}) 0.0 100.0 200.0 300.0 400.0 500.0
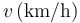
v\,(\mathrm{km}/\mathrm{h}) 108 90 72 54 36 18
  1. ¿Qué ley sencilla cumple la velocidad como función de la posición?
  2. Determine la aceleración como función de x. ¿Se trata de un movimiento uniformemente acelerado?
  3. Halle el valor de la aceleración en cada uno de los puntos de medida.
  4. Calcule el tiempo empleado en recorrer los 500 m. Si continúa con este movimiento, ¿cuánto tardará en recorrer 600 m?

1.8 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

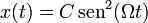
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

1.9 Frenado de un fórmula 1

Cuando el Ferrari de Sebastian Vettel se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 288 km/h. Cuando entra en la chicane va a 72 km/h.

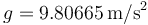  1. Suponiendo que la aceleración es constante, determine su valor. Exprese el resultado en el SI y como un múltiplo de g (siendo g=9.80665\,\mathrm{m}/\mathrm{s}^2).
  2. Determine la velocidad como función de la posición y represéntela gráficamente.
  3. Si el McLaren de Fernando Alonso va a 180 km/h a 150m de la chicane y se detiene a 50m de ésta, ¿es su aceleración mayor o menor que la de Vettel, en valor absoluto?

1.10 Estudio de un movimiento armónico simple

Un oscilador armónico con posición de equilibrio x = 0 se mueve de tal forma que en 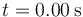t=0.00\,\mathrm{s} la partícula se halla en 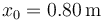x_0=0.80\,\mathrm{m}, moviéndose con velocidad 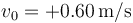v_0=+0.60\,\mathrm{m}/\mathrm{s} y aceleración 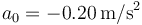a_0=-0.20\,\mathrm{m}/\mathrm{s}^2. Halle la frecuencia ω y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración.

1.11 Piedra y pájaro que se mueven verticalmente

Desde un punto a una altura 1.4 m respecto al suelo, un niño lanza verticalmente una piedra contra un pájaro que está 1.6 m más arriba. La velocidad inicial de la piedra es de 7.0 m/s. Tal como lanza la piedra, el pájaro sale volando hacia arriba con velocidad constante v1.

Despreciando el rozamiento del aire sobre la piedra y tomando g = 9.8 m/s²:

  1. Calcule el máximo valor de v1 con que asciende el pájaro, si la piedra es capaz de alcanzarle.
  2. Suponiendo que ha volado con esta velocidad máxima, calcule la velocidad instantánea de la piedra y del pájaro en el momento del impacto, así como la velocidad media de cada uno desde el lanzamiento hasta ese momento.
  3. Si en lugar de darle la piedra falla por poco y continúa su vuelo, ¿hasta que altura respecto al suelo llega? ¿Qué velocidad tiene cuando impacta de nuevo con el suelo?

1.12 Calculo gráfico de velocidad media

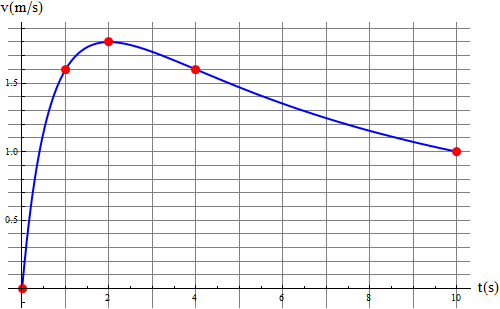
La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

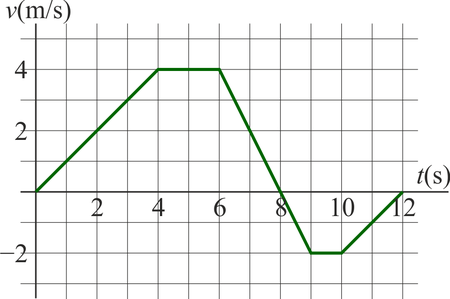
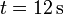  1. ¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?
  2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?
  3. De los cuatro instantes siguientes, ¿en cual la aceleración tiene el mayor valor absoluto? (a) 0.0 s; (b) 5.0 s; (c) 8.0 s; (d) 9.5 s.

2 Problemas adicionales

2.1 Movimiento con datos numéricos

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.00 0.25 0.50 0.75 1.00 1.25 1.50
x (m) 0.000 6.125 9.750 11.250 11.000 9.375 6.750


t (s) 1.75 2.00 2.25 2.50 2.75 3.00
x (m) 3.500 0.000 -3.375 -6.250 -8.250 -9.000

Para este movimiento, halle:

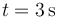  1. El desplazamiento entre t = 0\,\mathrm{s} y t=3\,\mathrm{s}, así como el valor aproximado de la distancia recorrida en dicho intervalo.
  2. La velocidad media y la rapidez media en el intervalo anterior.
  3. El valor aproximado de la velocidad en t= 2\,\mathrm{s}.
  4. El valor aproximado de la aceleración en t= 2\,\mathrm{s}.
  5. Sabiendo que este movimiento sigue una ley de la forma
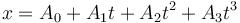
x = A_0 + A_1 t + A_2 t^2 + A_3 t^3\,
Calcule
  1. Los valores de las constantes Ak.
  2. El valor exacto de la distancia recorrida y la rapidez media.
  3. El valor exacto de la velocidad y de la aceleración en t = 2\,\mathrm{s}.

2.2 Aproximación numérica de la velocidad y la aceleración

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
x (m) 0.00 -0.04 -0.06 -0.06 -0.04 0.00 0.06 0.14 0.24 0.36 0.50
  1. ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre t=0\,\mathrm{s} y t=1\,\mathrm{s}.
  2. Calcule aproximadamente la aceleración en el mismo intervalo.

2.3 Integración aproximada de la velocidad

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

Archivo:graf-vt.png

La partícula parte de x = 0.

  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=10\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad, en el SI, es
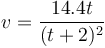
v = \frac{14.4t}{(t+2)^2}
¿Cuál es el error relativo cometido en el apartado anterior?
  1. Con ayuda de la cuadrícula halle el valor aproximado de la aceleración en 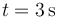t = 3\,\mathrm{s}. Calcule el valor exacto y el error cometido con la aproximación.

2.4 Ejemplo de integración numérica

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

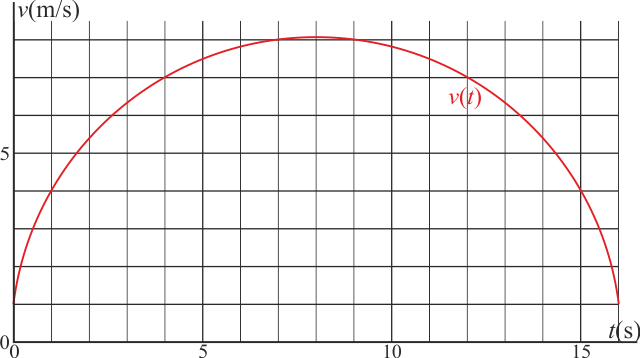
Archivo:velocidad-circulo.png

La partícula parte de s = 0.

  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=16\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es
v = \sqrt{1+16t-t^2}
¿Cuál es el error relativo cometido en el apartado anterior?

3 Preguntas de test

3.1 Identificación de movimiento

Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

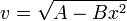
v = \sqrt{A- B x^2}

con A y B constantes positivas. La aceleración de una partícula que obedece esta ecuación es…

  • A proporcional a la posición x.
  • B nula.
  • C constante no nula.
  • D una combinación complicada de raíces cuadradas y polinomios.

3.2 Movimiento definido a trozos

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

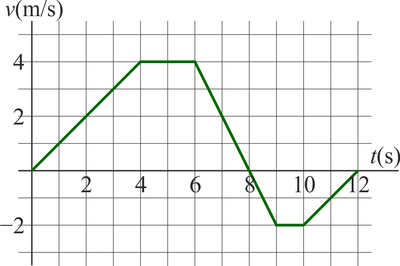
¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?

  • A 0.00 m/s
  • B 2.08 m/s
  • C 1.00 m/s
  • D 1.25 m/s

¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

  • A 15.0 m.
  • B 0.0 m
  • C 25.0 m.
  • D 12.0 m

De los cuatro instantes siguientes, ¿en cual la aceleración tiene el mayor valor absoluto?

  • A 0.0 s
  • B 5.0 s
  • C 8.0 s
  • D 9.5 s

3.3 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

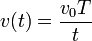
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre 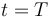t=T\, y t=3T\,?

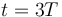  • A 0.667v0
  • B 0.500v0
  • C 0.549v0
  • D No hay información suficiente para determinarla.

3.4 Propiedades de un m.a.s.

Una partícula describe un movimiento armónico simple de frecuencia angular ω, pudiéndose mover a lo largo de una recta horizontal. En t = 0 pasa por la posición de equilibrio con una velocidad + v0.

¿Cuánto vale la velocidad media entre t = 0 y t = T / 4, con T el periodo de oscilación?

  • A 2v0 / π
  • B Es nula.
  • C v0 / 4
  • D v0 / 2

¿Cuánto vale la aceleración en t = T / 4?

  • A + 4v0 / T
  • B Es nula.
  • C − 4v0 / T
  • D − v0ω

3.5 Movimiento con dependencia exponencial

En un movimiento rectilíneo en el que la velocidad depende de la posición como

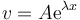
v = A\mathrm{e}^{\lambda x}\,

¿cuánto vale la aceleración?

  • A a = 0
  • B a = Aλeλx
  • C a = A2λe2λx
  • C a = A2e2λx / 2

3.6 Gráfica de una aceleración

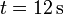La gráfica de la figura representa la aceleración de un movimiento rectilíneo entre t = 0\,\mathrm{s} y t=12\,\mathrm{s}. La partícula parte del reposo en x = 0.

Archivo:aceleracion-recta.png

¿Cuánto vale la rapidez en 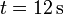t=12\,\mathrm{s}?

  • A 36 m/s.
  • B Es nula.
  • C 18 m/s.
  • D 72 m/s.

¿Cuánto vale la rapidez en t=6\,\mathrm{s}?

  • A 36 m/s.
  • B Es nula.
  • C 18 m/s.
  • D 72 m/s.

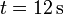¿Cuál es el desplazamiento neto entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?

  • A 72 m.
  • B 144 m.
  • C 0 m.
  • D -432 m.

3.7 Estudio de un m.a.s.

Una partícula describe un movimiento armónico simple alrededor de x = 0 tal que comienza en la posición de equilibrio con velocidad +0.40 m/s alcanzando el máximo alejamiento en t=2\,\mathrm{s}

¿Cuánto vale la amplitud del movimiento?

  • A 0.31 m
  • B No hay información suficiente para hallarla
  • C 0.80 m
  • D 0.51 m

¿Cuánto vale la aceleración cuando pasa por 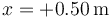x=+0.50\,\mathrm{m}?

  • A +0.20m/s²
  • B -0.31m/s²
  • C Es nula.
  • D −0.20m/s²

¿Cuánto tiempo tarda en pasa por primera vez por 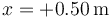x=+0.50\,\mathrm{m}?

  • A 1.25 s
  • B 1.76 s
  • C 0.80 s
  • D Nunca llega a esa posición.

3.8 Velocidad cuadrática con la posición

Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto v = − kx2. Su posición inicial es x(t = 0) = x0

¿Cuáles son las unidades de k en el SI?

  • A 1/(m·s)
  • B m³/s
  • C m/s
  • D m/s²

¿Cuánto vale la aceleración de la partícula cuando se halla en un punto x?

  • A 0
  • B 2k2x3
  • C No hay información suficiente para calcularla.
  • D − 2kx

¿Cuánto vale la posición como función del tiempo?

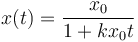
  • A x(t)=\displaystyle \frac{x_0}{1+kx_0t}
  • B x(t) = x0 − kx2t
  • C No hay información suficiente para calcularla.
  • D x(t) = x0e − kt

3.9 Fasor de un movimiento armónico

Una partícula describe un movimiento armónico simple con frecuencia angular 2 rad/s, siendo el fasor de la elongación 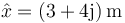\hat{x}=(3+4\mathrm{j})\,\mathrm{m}. ¿Cuánto vale su velocidad inicial?

  • A No hay información suficiente para determinarla.
  • B 2 m/s
  • C −8 m/s
  • D −2 m/s

3.10 Caso de movimiento armónico simple

Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI,

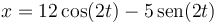
x = 12\cos(2t)-5\,\mathrm{sen}(2t)

¿Cuanto vale la amplitud de las oscilaciones?

  • A 13 m.
  • B 12 m.
  • C 5 m.
  • D 7 m.

¿Cuánto vale la velocidad inicial?

  • A −24 m/s.
  • B −2.5 m/s.
  • C −5 m/s.
  • D −10 m/s.

3.11 Movimiento conocida la velocidad

Una partícula describe un movimiento rectilíneo cuya velocidad, como función del tiempo entre t=0\,\mathrm{s} y t=10\,\mathrm{s} es la de la figura

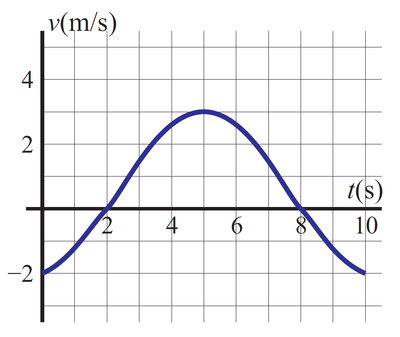
¿Cuánto vale, aproximadamente, el desplazamiento neto en el intervalo [0 s,10 s]?

  • A 30 m.
  • B 9 m.
  • C 5 m
  • D 13 m.

¿En qué intervalos, en s, la partícula está frenando?

  • A en 5<t<10.
  • B en 0<t<2 y 5<t<8
  • C en 2<t<5 y 8<t<10
  • D en 0<t<2 y 8<t<10

3.12 Velocidad a partir de fasor

El fasor de la posición de una partícula que describe un movimiento armónico simple de frecuencia angular 2 rad/s es 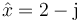\hat{x}=2-\mathrm{j}. ¿Cuánto vale su velocidad como función del tiempo?

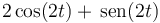
  • A 2\cos(2t)+\,\mathrm{sen}(2t)
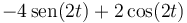
  • B -4\,\mathrm{sen}(2t)+2\cos(2t)
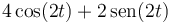
  • C 4\cos(2t)+2\,\mathrm{sen}(2t)
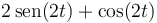
  • D 2\,\mathrm{sen}(2t)+\mathrm{cos}(2t)

3.13 Caso de m.a.s

Una partícula describe el movimiento armónico simple de ecuación, en el SI

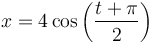
x=4\cos\left(\frac{t+\pi}{2}\right)

¿Cuánto vale su velocidad media entre t = 0 y t = 2π?

  • A 4/π m/s
  • B 2/π m/s
  • C −4/π m/s
  • D 0 m/s

¿Cuál es el fasor de la posición en este movimiento?

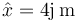
  • A \hat{x} = 4\mathrm{j}\,\mathrm{m}
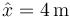
  • B \hat{x} = 4\,\mathrm{m}
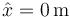
  • C \hat{x} = 0\,\mathrm{m}
  • D \hat{x} = -4\mathrm{j}\,\mathrm{m}

3.14 Viaje en dos fases

El crucero espacial Axiom realiza un viaje de 30 días. Para comodidad de sus pasajeros, parte del reposo y acelera durante 15 días con una aceleración constante g. A partir de ese punto comienza a frenar con la misma aceleración en valor absoluto, hasta detenerse de nuevo. ¿Cuál de las siguientes gráficas representa la posición de la nave con el tiempo?

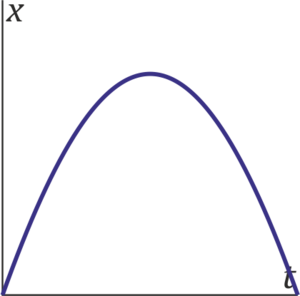
A B
C D

3.15 Aceleración definida a trozos

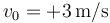Una partícula se mueve sobre una recta partiendo desde x_0=-5\,\mathrm{m} con velocidad v_0=+3\,\mathrm{m}/\mathrm{s}. En su movimiento, experimenta la aceleración

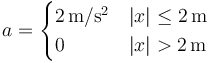
a=\begin{cases}2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}

¿Qué velocidad tiene cuando llega al punto x=+7\,\mathrm{m}?

  • A +3.0 m/s
  • B Nunca llega a ese punto.
  • C +5.0 m/s
  • D +6.1 m/s

¿Cuál es la velocidad media en todo el trayecto?

  • A 5 m/s
  • B 8 m/s
  • C 3 m/s
  • D 4 m/s

3.16 Cálculo de fasor

Un oscilador armónico tiene frecuencia ω, siendo el fasor de su posición 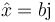\hat{x}=b\mathrm{j}. ¿Cuánto vale el fasor de la velocidad?

  • A \hat{v}=-\omega b
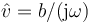
  • B \hat{v}=b/(\mathrm{j}\omega)
  • C \hat{v}=(\mathrm{d}b/\mathrm{d}t)\mathrm{j}
  • D \hat{v}=b/\omega

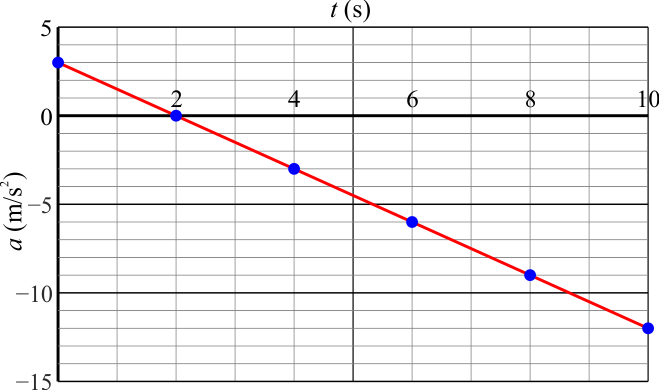
3.17 Partícula con aceleración variable

Una partícula de masa 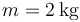m=2\,\mathrm{kg} describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en t=0\,\mathrm{s} del reposo en x = 0.

Archivo:aceleracion-lineal-t.png

¿Qué trabajo se realiza sobre ella entre t=0\,\mathrm{s} y t=10\,\mathrm{s}?

  • A 0J.
  • B 2025J
  • C No hay información suficiente para saberlo
  • D −2025J

¿Cuál es su velocidad media entre t=0\,\mathrm{s} y t=10\,\mathrm{s}?

  • A −3.75 m/s
  • B −10 m/s
  • C −22.5 m/s
  • D −60 m/s

¿En qué instante(s) del intervalo 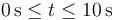0\,\mathrm{s}\leq t \leq 10\,\mathrm{s} es nula la potencia desarrollada sobre la partícula?

  • A Solo en t=2\,\mathrm{s}.
  • B Solo en t=0\,\mathrm{s} y en t=2\,\mathrm{s}.
  • C Solo en t=0\,\mathrm{s}.
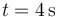
  • D En t=0\,\mathrm{s}, en t=2\,\mathrm{s} y t=4\,\mathrm{s}

¿Cuál es la distancia total recorrida t=0\,\mathrm{s} y t=10\,\mathrm{s}?

  • A −600 m
  • B −100 m
  • C 100 m
  • D 116 m

3.18 Velocidad variable

Una partícula describe un movimiento rectilíneo en el que parte del reposo con velocidad inicial v0 y su aceleración varía con el tiempo como

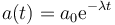
a(t)=a_0\mathrm{e}^{-\lambda t}\,

con a0 y λ constantes positivas.

¿Cómo cambia la velocidad de esta partícula con el tiempo?

  • A aumenta indefinidamente hasta infinito.
  • B disminuye indefinidamente hasta -\infty.
  • C aumenta continuamente, tendiendo a un valor constante.
  • D disminuye gradualmente hasta cero.

3.19 Velocidad media

En un movimiento rectilíneo, la velocidad de una partícula como función del tiempo sigue la gráfica de la figura. ¿Cuánto vale la velocidad media en este intervalo de tiempo?

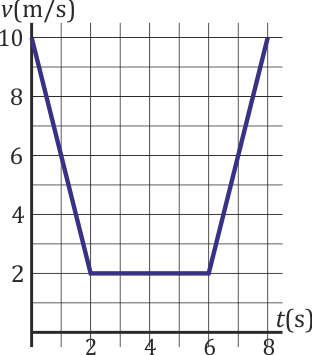
Archivo:v-quebrada.png
  • A 6 m/s
  • B 5 m/s
  • C 4 m/s
  • D 10 m/s

3.20 Caso de m.a.s.

En un movimiento armónico simple de frecuencia 3 rad/s la amplitud compleja o fasor de la velocidad es 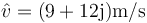\hat{v}=(9+12\mathrm{j})\mathrm{m}/\mathrm{s}.

¿Cuanto vale la velocidad inicial de la partícula?

  • A 3 m/s
  • B 9 m/s
  • C 4 m/s
  • D 36 m/s

Para este movimiento, ¿cuánto vale la amplitud de las oscilaciones?

  • A 5 m
  • B 15 m
  • C 3 m
  • D 4 m

3.21 Velocidad media

Una partícula se mueve a lo largo del eje OX con la velocidad instantánea v(t) = Bt2 Si V es la velocidad instantánea en t = T, y vm es la velocidad media entre t = 0 y t = T se cumple

  • A vm = V / 2.
  • B vm = V / 3.
  • C vm = V.
  • D vm = 2V / 3.

3.22 Velocidad inversamente proporcional a la posición

En un movimiento rectilíneo, la velocidad de una partícula sigue la ley como función de la posición v = K / x. Inicialmente se encuentra en x0. ¿Qué ley sigue la posición como función del tiempo?

  • A x(t) = (K / x0)t + x0
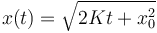
  • B x(t)=\sqrt{2Kt+x_0^2}
  • C x(t) = x0
  • D x(t) = x0 − (K / x0)t
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_movimiento_rectil%C3%ADneo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:56, 18 ago 2018. - Esta página ha sido visitada 46.605 veces. - Aviso legal - Acerca de Laplace