Preguntas de test de cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Identificación de movimiento
2 Movimiento definido a trozos
- 2.1 Pregunta 1
- 2.2 Pregunta 2
- 2.3 Pregunta 3
3 Cálculo de velocidad media
4 Propiedades de un m.a.s.
- 4.1 Pregunta 1
- 4.2 Pregunta 2
5 Movimiento con dependencia exponencial
6 Gráfica de una aceleración
- 6.1 Pregunta 1
- 6.2 Pregunta 2
- 6.3 Pregunta 3
7 Estudio de un m.a.s.
- 7.1 Pregunta 1
- 7.2 Pregunta 2
- 7.3 Pregunta 3
8 Velocidad cuadrática con la posición
- 8.1 Pregunta 1
- 8.2 Pregunta 2
- 8.3 Pregunta 3
9 Fasor de un movimiento armónico
10 Caso de movimiento armónico simple
- 10.1 Pregunta 1
- 10.2 Pregunta 2
11 Movimiento conocida la velocidad
- 11.1 Pregunta 1
- 11.2 Pregunta 2
12 Velocidad a partir de fasor
13 Caso de m.a.s.
- 13.1 Pregunta 1
- 13.2 Pregunta 2
14 Viaje en dos fases
15 Aceleración definida a trozos
- 15.1 Pregunta 1
- 15.2 Pregunta 2
16 Cálculo de fasor
17 Partícula con aceleración variable
- 17.1 Pregunta 1
- 17.2 Pregunta 2
- 17.3 Pregunta 3
- 17.4 Pregunta 4
18 Velocidad variable
19 Velocidad media
20 Caso de m.a.s.
- 20.1 Pregunta 1
- 20.2 Pregunta 2
21 Velocidad media
22 Velocidad inversamente proporcional a la posición

1 Identificación de movimiento

Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

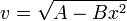
$v = \sqrt{A- B x^2}$

con $A$ y $B$ constantes positivas. La aceleración de una partícula que obedece esta ecuación es…

A proporcional a la posición x.
B nula.
C constante no nula.
D una combinación complicada de raíces cuadradas y polinomios.

Solución

La respuesta correcta es la A.

La aceleración en este movimiento vale

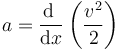
$a=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{v^2}{2}\right)$

siendo

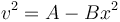
$v^2 = A - Bx^2\,$

nos queda

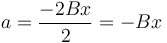
$a = \frac{-2Bx}{2}=-Bx$

Vemos que la aceleración es proporcional a la posición. Es más, se trata de un oscilador armónico.

2 Movimiento definido a trozos

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

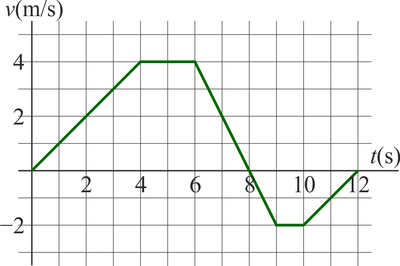
2.1 Pregunta 1

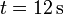¿Cuánto vale aproximadamente la velocidad media entre $t=0\,\mathrm{s}$ y $t=12\,\mathrm{s}$ ?

A 0.00 m/s
B 2.08 m/s
C 1.00 m/s
D 1.25 m/s

Solución

La respuesta correcta es la D.

La velocidad media la calculamos como la distancia recorrida dividida por el tiempo empleado en recorrerla

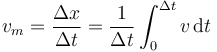
$v_m=\frac{\Delta x}{\Delta t}=\frac{1}{\Delta t}\int_0^{\Delta t}v\,\mathrm{d}t$

El desplazamiento es la integral de la velocidad instantánea,

lo que da en este caso

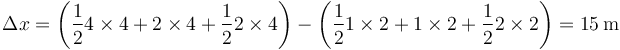
$\Delta x = \left(\frac{1}{2}4\times 4 +2\times 4+\frac{1}{2}2\times 4\right)-\left(\frac{1}{2}1\times 2+1\times 2+\frac{1}{2}2\times 2\right)=15\,\mathrm{m}$

y queda la velocidad media

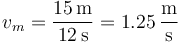
$v_m=\frac{15\,\mathrm{m}}{12\,\mathrm{s}}=1.25\,\frac{\mathrm{m}}{\mathrm{s}}$

2.2 Pregunta 2

¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

A 15.0 m.
B 0.0 m
C 25.0 m.
D 12.0 m

Solución

La respuesta correcta es la C.

La distancia recorrida es la integral de la rapidez o celeridad

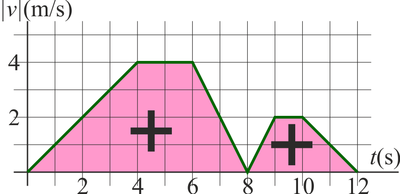
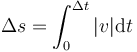
$\Delta s=\int_0^{\Delta t}|v|\mathrm{d}t$

que en este caso da

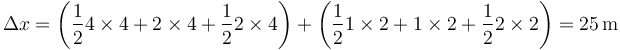
$\Delta x = \left(\frac{1}{2}4\times 4 +2\times 4+\frac{1}{2}2\times 4\right)+\left(\frac{1}{2}1\times 2+1\times 2+\frac{1}{2}2\times 2\right)=25\,\mathrm{m}$

2.3 Pregunta 3

De los cuatro instantes siguientes, ¿en cual la aceleración tiene el mayor valor absoluto?

A 0.0 s
B 5.0 s
C 8.0 s
D 9.5 s

Solución

La respuesta correcta es la C.

La máxima velocidad se alcanza cuando sea mayor la pendiente de la gráfica $x (t)$ , lo cual ocurre en 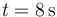$t=8\,\mathrm{s}$ .

3 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

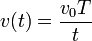
$v(t) = \frac{v_0T}{t}$

¿Cuánto vale la velocidad media entre $t = T$ y $t = 3 T$ ?

A $0.667 v 0$
B $0.500 v 0$
C $0.549 v 0$
D No hay información suficiente para determinarla.

Solución

La respuesta correcta es la C.

La velocidad media en un intervalo es igual al cociente entre el desplazamiento realizado en un intervalo y la duración de este intervalo

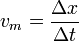
$v_m = \frac{\Delta x}{\Delta t}$

La duración del intervalo es la diferencia entre el instante inicial final y el inicial

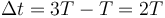
$\Delta t = 3T-T = 2T\,$

mientras que el desplazamiento es la suma de los desplazamientos infinitesimales, y por tanto igual a la integral de la velocidad instantánea

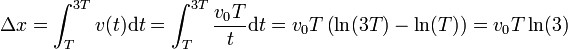
$\Delta x = \int_T^{3T} v(t)\mathrm{d}t = \int_T^{3T}\frac{v_0T}{t}\mathrm{d}t = v_0T\left(\ln(3T)-\ln(T)\right)=v_0T\ln(3)$

La velocidad media vale entonces

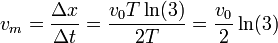
$v_m = \frac{\Delta x}{\Delta t} = \frac{v_0T\ln(3)}{2T}=\frac{v_0}{2}\ln(3)$

cuyo valor numérico es

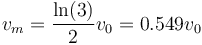
$v_m = \frac{\ln(3)}{2}v_0 = 0.549v_0$

4 Propiedades de un m.a.s.

Una partícula describe un movimiento armónico simple de frecuencia angular $ω$ , pudiéndose mover a lo largo de una recta horizontal. En $t = 0$ pasa por la posición de equilibrio con una velocidad $+ v 0$ .

4.1 Pregunta 1

¿Cuánto vale la velocidad media entre $t = 0$ y $t = T / 4$ , con $T$ el periodo de oscilación?

A $2 v 0 / π$
B Es nula.
C $v 0 / 4$
D $v 0 / 2$

Solución

La respuesta correcta es la A.

La velocidad media de una partícula en un movimiento rectilíneo se calcula como el cociente entre el desplazamiento neto y la duración del intervalo en que se realiza

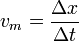
$v_m = \frac{\Delta x}{\Delta t}$

En este caso, el intervalo se nos da como dato: es la cuarta parte del periodo

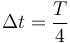
$\Delta t = \frac{T}{4}$

En un movimiento armónico simple, una partícula que parte del punto de equilibrio en $t = 0$ alcanza la máxima elongación en $T / 4$ ; en $T / 2$ vuelve a pasar por el origen en $3 T / 4$ alcanza la distancia máxima por el lado opuesto y en $T$ regresa al origen, completando el ciclo.

Por tanto el desplazamiento entre $t = 0$ y $t = T / 4$ es igual a la elongación máxima, es decir a la amplitud.

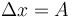
$\Delta x = A\,$

y la velocidad media será igual a

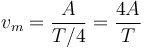
$v_m = \frac{A}{T/4} = \frac{4A}{T}$

Queda calcular la amplitud a partir de los datos del enunciado.

Tenemos que la ecuación general de un movimiento armónico simple es

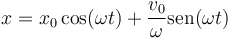
$x = x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

En esta ocasión la posición inicial es nula y el movimiento se reduce a un seno, como en la gráfica anterior

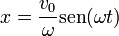
$x = \frac{v_0}{\omega}\mathrm{sen}(\omega t)$

La máxima elongación se da cuando el seno vale 1, por lo que la amplitud vale

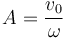
$A = \frac{v_0}{\omega}$

y queda la velocidad media

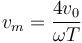
$v_m = \frac{4v_0}{\omega T}$

pero

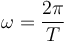
$\omega = \frac{2\pi}{T}$

lo que nos da finalmente

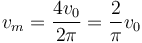
$v_m = \frac{4v_0}{2\pi} = \frac{2}{\pi}v_0$

4.2 Pregunta 2

¿Cuánto vale la aceleración en $t = T / 4$ ?

A $+ 4 v 0 / T$
B Es nula.
C $- 4 v 0 / T$
D $- v 0 ω$

Solución

La respuesta correcta es la D.

La aceleración en un movimiento armónico simple tiene la expresión

a = - ω 2 x

con $x$ la posición medida respecto a la de equilibrio. En $t = T / 4$ la elongación es la máxima y

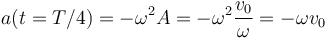
$a(t=T/4) = -\omega^2 A = -\omega^2 \frac{v_0}{\omega} = -\omega v_0$

5 Movimiento con dependencia exponencial

En un movimiento rectilíneo en el que la velocidad depende de la posición como

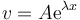
$v = A\mathrm{e}^{\lambda x}\,$

¿cuánto vale la aceleración?

A $a = 0$
B $a = A λe λ x$
C $a = A 2 λe 2λ x$
C $a = A 2 e 2λ x / 2$

Solución

La respuesta correcta es la C.

Hallamos la aceleración calculando la derivada de la velocidad respecto al tiempo, lo cual se consigue aplicando la regla de la cadena

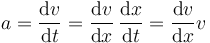
$a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}x}v$

lo que da

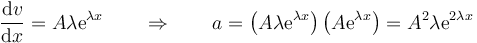
$\frac{\mathrm{d}v}{\mathrm{d}x}=A\lambda\mathrm{e}^{\lambda x}\qquad\Rightarrow\qquad a = \left(A\lambda\mathrm{e}^{\lambda x}\right)\left(A\mathrm{e}^{\lambda x}\right)=A^2\lambda\mathrm{e}^{2\lambda x}$

Alternativamente, podemos calcularlo directamente a partir de

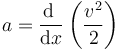
$a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{v^2}{2}\right)$

queda

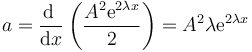
$a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{A^2\mathrm{e}^{2\lambda x}}{2}\right) = A^2\lambda\mathrm{e}^{2\lambda x}$

6 Gráfica de una aceleración

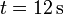La gráfica de la figura representa la aceleración de un movimiento rectilíneo entre $t = 0\,\mathrm{s}$ y $t=12\,\mathrm{s}$ . La partícula parte del reposo en $x = 0$ .

6.1 Pregunta 1

¿Cuánto vale la rapidez en 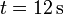$t=12\,\mathrm{s}$ ?

A 36 m/s.
B Es nula.
C 18 m/s.
D 72 m/s.

Solución

La respuesta correcta es la B.

La ecuación de esta aceleración es, en el SI,

$a(t) = 6-t\,$

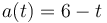
que integrada nos da la velocidad instantánea

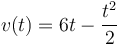
$v(t) = 6t - \frac{t^2}{2}\,$

En t = 12s esta velocidad vale

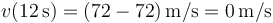
$v(12\,\mathrm{s}) =(72-72)\,\mathrm{m}/\mathrm{s}=0\,\mathrm{m}/\mathrm{s}$

con lo que la rapidez en ese instante es también nula. Gráficamente esto quiere decir que en la gráfica de la aceleración, el área sobre el eje equivale al área bajo él.

6.2 Pregunta 2

¿Cuánto vale la rapidez en $t=6\,\mathrm{s}$ ?

A 36 m/s.
B Es nula.
C 18 m/s.
D 72 m/s.

Solución

La respuesta correcta es la C.

Para este instante, en cambio

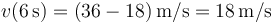
$v(6\,\mathrm{s}) = (36-18)\,\mathrm{m}/\mathrm{s}=18\,\mathrm{m}/\mathrm{s}$

que también es el valor de la rapidez en ese instante.

6.3 Pregunta 3

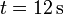¿Cuál es el desplazamiento neto entre $t=0\,\mathrm{s}$ y $t=12\,\mathrm{s}$ ?

A 72 m.
B 144 m.
C 0 m.
D -432 m.

Solución

La respuesta correcta es la B.

Para hallar el desplzamiento debemos integrar la velocidad, con el resultado

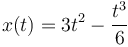
$x(t) = 3t^2 -\frac{t^3}{6}$

que en t=12s vale

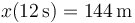
$x(12\,\mathrm{s}) = 144\,\mathrm{m}$

Puesto que la posición inicial es x=0, el desplazamiento en este intervalo es

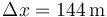
$\Delta x = 144\,\mathrm{m}$

7 Estudio de un m.a.s.

Una partícula describe un movimiento armónico simple alrededor de $x = 0$ tal que comienza en la posición de equilibrio con velocidad +0.40 m/s alcanzando el máximo alejamiento en $t=2\,\mathrm{s}$

7.1 Pregunta 1

¿Cuánto vale la amplitud del movimiento?

A 0.31 m
B No hay información suficiente para hallarla
C 0.80 m
D 0.51 m

Solución

La respuesta correcta es la D.

Si la partícula parte de la posición de equilibrio con una cierta velocidad, la ecuación horaria es, como en una pregunta anterior

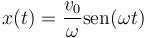
$x(t)=\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

siendo la amplitud del movimiento

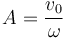
$A = \frac{v_0}{\omega}$

La frecuencia angular la obtenemos del periodo

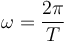
$\omega = \frac{2\pi}{T}$

donde el dato que nos dan es el tiempo que tarda en alcanzar el máximo. Esto ocurre en T/4, por lo que

$T = 4\times(2\mathrm{s})=8\,\mathrm{s}\qquad\qquad\omega = \frac{\pi}{4}\mathrm{s}^{-1}=0.785\,\mathrm{s}^{-1}$

y queda la amplitud

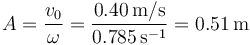
$A=\frac{v_0}{\omega}=\frac{0.40\,\mathrm{m}/\mathrm{s}}{0.785\,\mathrm{s}^{-1}}=0.51\,\mathrm{m}$

7.2 Pregunta 2

¿Cuánto vale la aceleración cuando pasa por 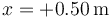$x=+0.50\,\mathrm{m}$ ?

A +0.20m/s²
B -0.31m/s²
C Es nula.
D −0.20m/s²

Solución

La respuesta correcta es la B.

La aceleración en un oscilador armónico es proporcional a la posición

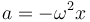
$a = -\omega^2 x\,$

lo que en este caso vale

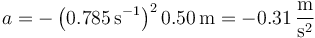
$a = -\left(0.785\,\mathrm{s}^{-1}\right)^2 0.50\,\mathrm{m}=-0.31\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Es fácil ver que esta es la respuesta correcta, ya que por la ecuación del oscilador armónico, la aceleración en un punto de coordenada positiva debe ser negativa, y esta es la única solución de ese tipo.

7.3 Pregunta 3

¿Cuánto tiempo tarda en pasar por primera vez por 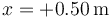$x=+0.50\,\mathrm{m}$ ?

A 1.25 s
B 1.76 s
C 0.80 s
D Nunca llega a esa posición.

Solución

La respuesta correcta es la B.

Volvemos a la ecuación del movimiento armónico simple para este caso

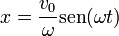
$x = \frac{v_0}{\omega}\mathrm{sen}(\omega t)$

y despejamos el tiempo que tarda en llegar a una posición dada

$t = \frac{1}{\omega}\mathrm{arcsen}\left(\frac{\omega x}{v_0}\right)$

siendo su valor numérico

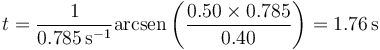
$t = \frac{1}{0.785\,\mathrm{s}^{-1}}\mathrm{arcsen}\left(\frac{0.50\times 0.785}{0.40}\right) = 1.76\,\mathrm{s}$

8 Velocidad cuadrática con la posición

Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto $v = - k x 2$ . Su posición inicial es $x (t = 0) = x 0$

8.1 Pregunta 1

¿Cuáles son las unidades de $k$ en el SI

A 1/(m·s)
B m³/s
C m/s
D m/s²

Solución

La respuesta correcta es la A.

Por homogeneidad dimensional

$1\,\frac{\mathrm{m}}{\mathrm{s}}=[k]\left(1\,\mathrm{m}\right)^2 \qquad\Rightarrow\qquad [k]=\frac{1}{\mathrm{m}\cdot\mathrm{s}}$

8.2 Pregunta 2

¿Cuánto vale la aceleración de la partícula cuando se halla en un punto $x$ ?

A 0
B $2 k 2 x 3$
C No hay información suficiente para calcularla.
D $- 2 k x$

Solución

La respuesta correcta es la B.

Derivamos respecto al tiempo la velocidad, mediante la regla de la cadena

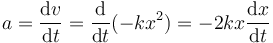
$a=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d} }{\mathrm{d}t}(-kx^2)=-2kx\frac{\mathrm{d}x}{\mathrm{d}t}$

pero la derivada de la posición respecto al tiempo es la propia velocidad

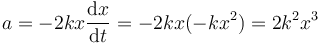
$a=-2kx\frac{\mathrm{d}x}{\mathrm{d}t}=-2kx(-kx^2) = 2k^2 x^3$

8.3 Pregunta 3

¿Cuánto vale la posición como función del tiempo?

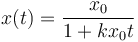
A $x(t)=\displaystyle \frac{x_0}{1+kx_0t}$
B $x (t) = x 0 - k x 2 t$
C No hay información suficiente para calcularla.
D $x (t) = x 0 e - k t$

Solución

La respuesta correcta es la A.

La velocidad es el cociente entre un desplazamiento diferencial y el intervalo que tarda en recorrerse

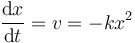
$\frac{\mathrm{d}x}{\mathrm{d}t}=v=-kx^2$

Esto quiere decir que el tiempo necesario para recorrer dx es, despejando,

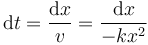
$\mathrm{d}t = \frac{\mathrm{d}x}{v}=\frac{\mathrm{d}x}{-kx^2}$

Sumando (es decir, integrando) todos los diferenciales obtenemos el tiempo necesario para llegar a una cierta posición

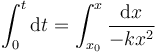
$\int_0^t \mathrm{d}t=\int_{x_0}^x \frac{\mathrm{d}x}{-kx^2}$

lo que da

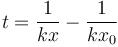
$t = \frac{1}{kx}-\frac{1}{kx_0}$

Despejamos de aquí x y da

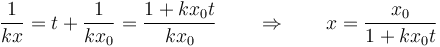
$\frac{1}{kx}=t+\frac{1}{kx_0}=\frac{1+kx_0 t}{kx_0}\qquad\Rightarrow\qquad x = \frac{x_0}{1+kx_0 t}$

Un método alternativo es operar a la inversa. Puesto que nos dan 4 posibles soluciones se trata de ver cuál cumple

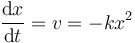
$\frac{\mathrm{d}x}{\mathrm{d}t}=v=-kx^2$

Derivamos la opción A

$v=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{x_0}{1+kx_0 t}\right)=-\frac{kx_0^2}{(1+kx_0t)^2}$

pero lo que está en el segundo miembro es igual a

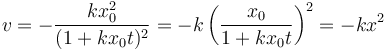
$v=-\frac{kx_0^2}{(1+kx_0t)^2}=-k\left(\frac{x_0}{1+kx_0 t}\right)^2 = -kx^2$

Si actuamos del mismo modo con las opciones B y D no llegamos a soluciones que verifiquen la ecuación dada.

9 Fasor de un movimiento armónico

Una partícula describe un movimiento armónico simple con frecuencia angular 2 rad/s, siendo el fasor de la elongación 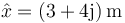$\hat{x}=(3+4\mathrm{j})\,\mathrm{m}$ $. ¿Cuánto vale su velocidad inicial?

A No hay información suficiente para determinarla.
B 2 m/s
C −8 m/s
D −2 m/s

Solución

La respuesta correcta es la C.

El fasor de un movimiento armónico simple es el número complejo

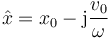
$\hat{x}=x_0-\mathrm{j}\frac{v_0}{\omega}$

con $x 0$ y $v 0$ la posición y velocidad inicial.

En este caso

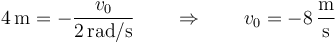
$4\,\mathrm{m}=-\frac{v_0}{2\,\mathrm{rad}/\mathrm{s}}\qquad\Rightarrow\qquad v_0=-8\,\frac{\mathrm{m}}{\mathrm{s}}$

10 Caso de movimiento armónico simple

Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI,

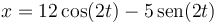
$x = 12\cos(2t)-5\,\mathrm{sen}(2t)$

10.1 Pregunta 1

¿Cuanto vale la amplitud de las oscilaciones?

A 13 m.
B 12 m.
C 5 m.
D 7 m.

Solución

La respuesta correcta es la A.

La solución general del m.a.s. puede escribirse en las formas

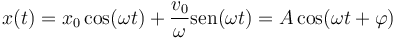
$x(t)=x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}(\omega t)=A\cos(\omega t +\varphi)$

La relación entre ambas se obtiene desarollando el coseno de una suma e identificando coeficientes

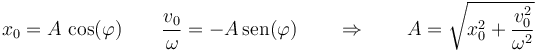
$x_0=A\,\cos(\varphi)\qquad \frac{v_0}{\omega}=-A\,\mathrm{sen}(\varphi)\qquad\Rightarrow\qquad A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$

En nuestro caso

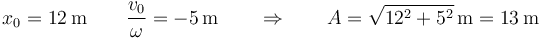
$x_0=12\,\mathrm{m}\qquad \frac{v_0}{\omega}=-5\,\mathrm{m}\qquad\Rightarrow\qquad A=\sqrt{12^2+5^2}\,\mathrm{m}=13\,\mathrm{m}$

10.2 Pregunta 2

¿Cuánto vale la velocidad inicial?

A −24 m/s.
B −2.5 m/s.
C −5 m/s.
D −10 m/s.

Solución

La respuesta correcta es la D.

Por las relaciones anteriores

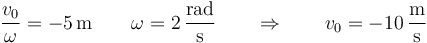
$\frac{v_0}{\omega}=-5\,\mathrm{m}\qquad \omega = 2\,\frac{\mathrm{rad}}{\mathrm{s}}\qquad\Rightarrow\qquad v_0=-10\,\frac{\mathrm{m}}{\mathrm{s}}$

11 Movimiento conocida la velocidad

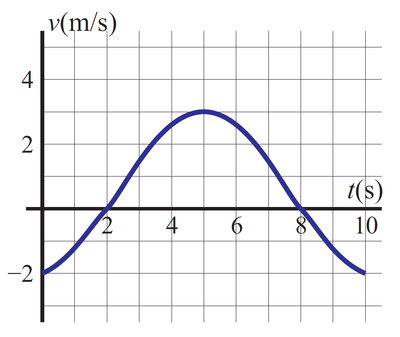
Una partícula describe un movimiento rectilíneo cuya velocidad, como función del tiempo entre $t=0\,\mathrm{s}$ y $t=10\,\mathrm{s}$ es la de la figura

11.1 Pregunta 1

¿Cuánto vale, aproximadamente, el desplazamiento neto en el intervalo [0 s,10 s]?

A 30 m.
B 9 m.
C 5 m
D 13 m.

Solución

La respuesta correcta es la C.

Para hallar la integral aproximamos la función por rectas, por lo que debemos sumar áreas de triángulos y queda

$\Delta x\sim -\frac{1}{2}2\times 2+\frac{1}{2}6\times 3 -\frac{1}{2}2\times 2=-2+9-2 =5\,\mathrm{m}$

11.2 Pregunta 2

¿En qué intervalos, en s, la partícula está frenando?

A en 5<t<10.
B en 0<t<2 y 5<t<8
C en 2<t<5 y 8<t<10
D en 0<t<2 y 8<t<10

Solución

La respuesta correcta es la B.

Está frenando siempre que la rapidez (valor absoluto de la velocidad) esté disminuyendo. Gráficamente son los tramos en que la función se acerca al eje (y acelera cuando se aleja de él).

Esto ocurre en 0s < t < 2s (donde la rapidez pasa de 2m/s a 0m/s) y en 5s < t < 8s (donde pasa de 3m/s a 0).

12 Velocidad a partir de fasor

El fasor de la posición de una partícula que describe un movimiento armónico simple de frecuencia angular 2 rad/s es 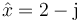$\hat{x}=2-\mathrm{j}$ . ¿Cuánto vale su velocidad como función del tiempo?

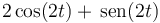
A $2\cos(2t)+\,\mathrm{sen}(2t)$
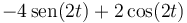
B $-4\,\mathrm{sen}(2t)+2\cos(2t)$
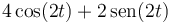
C $4\cos(2t)+2\,\mathrm{sen}(2t)$
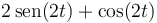
D $2\,\mathrm{sen}(2t)+\mathrm{cos}(2t)$

Solución

La respuesta correcta es la B.

El fasor de la posición es de la forma

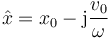
$\hat{x}=x_0-\mathrm{j}\frac{v_0}{\omega}$

y conduce a la posición como función del tiempo

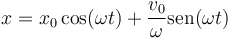
$x=x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

en este caso, en el SI,

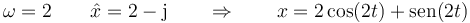
$\omega = 2\qquad \hat{x}=2-\mathrm{j}\qquad\Rightarrow\qquad x=2\cos(2t)+\mathrm{sen}(2t)$

Para hallar la velocidad, derivamos respecto al tiempo

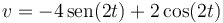
$v=-4\,\mathrm{sen}(2t)+2\cos(2t)$

Alternativamente, podemos evitar el derivar si primero calculamos el fasor de la velocidad

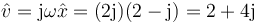
$\hat{v}=\mathrm{j}\omega\hat{x}=(2\mathrm{j})(2-\mathrm{j})=2+4\mathrm{j}$

y ahora aplicamos la fórmula de Euler

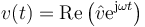
$v(t)=\mathrm{Re}\left(\hat{v}\mathrm{e}^{\mathrm{j}\omega t}\right)$

lo que da

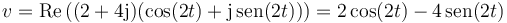
$v =\mathrm{Re}\left((2+4\mathrm{j})(\cos(2t)+\mathrm{j}\,\mathrm{sen}(2t))\right)=2\cos(2t)-4\,\mathrm{sen}(2t)$

13 Caso de m.a.s.

Una partícula describe el movimiento armónico simple de ecuación, en el SI

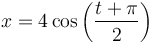
$x=4\cos\left(\frac{t+\pi}{2}\right)$

13.1 Pregunta 1

¿Cuánto vale su velocidad media entre $t = 0$ y $t = 2π$ ?

A 4/π m/s
B 2/π m/s
C −4/π m/s
D 0 m/s

Solución

La respuesta correcta es la D.

El desplazamiento que realiza la partícula es

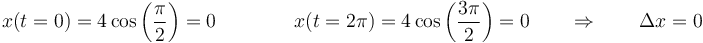
$x(t=0) = 4\cos\left(\frac{\pi}{2}\right)=0\qquad\qquad x(t=2\pi)=4\cos\left(\frac{3\pi}{2}\right)=0\qquad\Rightarrow\qquad \Delta x=0$

y por tanto la velocidad media es nula

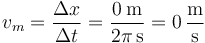
$v_m=\frac{\Delta x}{\Delta t}=\frac{0\,\mathrm{m}}{2\pi\,\mathrm{s}}=0\,\frac{\mathrm{m}}{\mathrm{s}}$

13.2 Pregunta 2

¿Cuál es el fasor de la posición en este movimiento?

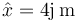
A $\hat{x} = 4\mathrm{j}\,\mathrm{m}$
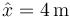
B $\hat{x} = 4\,\mathrm{m}$
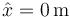
C $\hat{x} = 0\,\mathrm{m}$
D $\hat{x} = -4\mathrm{j}\,\mathrm{m}$

Solución

La respuesta correcta es la A.

Si aplicamos la fórmula de Euler queda

$x= 4\,\mathrm{Re}\left(\mathrm{e}^{\mathrm{j}(t+\pi)/2}\right)=\mathrm{Re}\left(4\mathrm{e}^{\mathrm{j}\pi/2}\mathrm{e}^{\mathrm{j}t/2}\right)$

que nos dice que el fasor de la elongación es

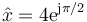
$\hat{x}=4\mathrm{e}^{\mathrm{j}\pi/2}$

pero por la misma fórmula de Euler

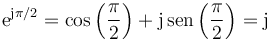
$\mathrm{e}^{\mathrm{j}\pi/2}=\cos\left(\frac{\pi}{2}\right)+\mathrm{j}\,\mathrm{sen}\left(\frac{\pi}{2}\right)=\mathrm{j}$

con lo que nos queda el fasor

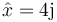
$\hat{x}=4\mathrm{j}$

14 Viaje en dos fases

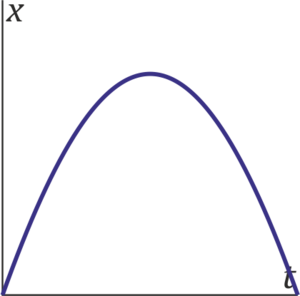
El crucero espacial Axiom realiza un viaje de 30 días. Para comodidad de sus pasajeros, parte del reposo y acelera durante 15 días con una aceleración constante $g$ . A partir de ese punto comienza a frenar con la misma aceleración en valor absoluto, hasta detenerse de nuevo. ¿Cuál de las siguientes gráficas representa la posición de la nave con el tiempo?

A	B


C	D

Solución

La respuesta correcta es la B.

La velocidad, que es la integral de la aceleración, es una función continua, y lo mismo ocurre con la posición, integral de la velocidad (la nave no se teletransporta). Por tanto la opción C no es correcta (salto en la posición) ni la D tampoco (salto en la velocidad, pendiente de la curva).

La opción A es siempre cóncava hacia abajo, lo cual quiere decir que su aceleración es siempre negativa, lo cual va en contra de lo que dice el enunciado. Aparte, la pendiente inicial y la final no son nulas, lo que contradice el que parte del reposo y termina parándose de nuevo.

Por tanto la correcta es la B, que tiene una primera mitad cóncava hacia arriba (aceleración positiva) y una segunda cóncava hacia abajo (aceleración negativa).

15 Aceleración definida a trozos

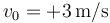Una partícula se mueve sobre una recta partiendo desde $x_0=-5\,\mathrm{m}$ con velocidad $v_0=+3\,\mathrm{m}/\mathrm{s}$ . En su movimiento, experimenta la aceleración

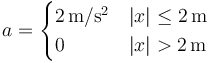
$a=\begin{cases}2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}$

15.1 Pregunta 1

¿Qué velocidad tiene cuando llega al punto $x=+7\,\mathrm{m}$ ?

A +3.0 m/s
B Nunca llega a ese punto.
C +5.0 m/s
D +6.1 m/s

Solución

La respuesta correcta es la C.

Esta pregunta (y la siguiente) se puede resolver empleando la ecuación del movimiento uniforme y del movimiento uniformemente acelerado, pero también empleando otras que evitan el cálculo en función del tiempo.

La aceleración en un movimiento uniformemente acelerado cumple

$a = \frac{v_2^2-v_1^2}{2(x_2-x_1)}$

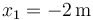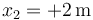La zona donde hay aceleración va de $x_1 = -2\,\mathrm{m}$ a $x_2 = +2\,\mathrm{m}$ , siendo la velocidad de entrada +3m/s y la aceleración +2m/s². Esto nos da, en el SI

$2 = \frac{v_2^2-3^2}{2\cdot 4}\qquad\Rightarrow\qquad v_2^2 = 25\qquad\Rightarrow\qquad v_2 = 5$

15.2 Pregunta 2

¿Cuál es la velocidad media en todo el trayecto?

A 5 m/s
B 8 m/s
C 3 m/s
D 4 m/s

Solución

La respuesta correcta es la D.

El movimiento se compone de tres tramos, siendo el desplazamiento total

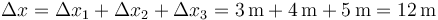
$\Delta x = \Delta x_1 + \Delta x_2 + \Delta x_3 = 3\,\mathrm{m}+4\,\mathrm{m}+5\,\mathrm{m}=12\,\mathrm{m}$

El primer tramo mide 3m y se recorre a una velocidad constante de 3m/s, por lo que

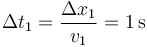
$\Delta t_1 = \frac{\Delta x_1}{v_1}=1\,\mathrm{s}$

El primer tramo mide 5m y se recorre a una velocidad constante de 5m/s, por lo que

$\Delta t_3 = \frac{\Delta x_3}{v_3}=1\,\mathrm{s}$

El segundo tramo se recorre con un movimiento uniformemente acelerado. Para este movimiento la velocidad media es

$v_{m2}=\frac{v_1+v_2}{2}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

y por tanto, el tiempo que se tarda en recorrer esta zona es

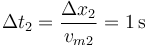
$\Delta t_2 = \frac{\Delta x_2}{v_{m2}}= 1\,\mathrm{s}$

Por tanto, el intervalo total dura

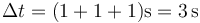
$\Delta t = (1+1+1)\mathrm{s}=3\,\mathrm{s}$

lo que nos da la velocidad media

$v_m = \frac{\Delta x}{\Delta t}=\frac{12\,\mathrm{m}}{3\,\mathrm{s}}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

16 Cálculo de fasor

Un oscilador armónico tiene frecuencia $ω$ , siendo el fasor de su posición 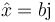$\hat{x}=b\mathrm{j}$ . ¿Cuánto vale el fasor de la velocidad?

A $\hat{v}=-\omega b$
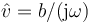
B $\hat{v}=b/(\mathrm{j}\omega)$
C $\hat{v}=(\mathrm{d}b/\mathrm{d}t)\mathrm{j}$
D $\hat{v}=b/\omega$

Solución

La respuesta correcta es la A.

El fasor de la velocidad cumple

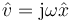
$\hat{v}=\mathrm{j}\omega\hat{x}$

17 Partícula con aceleración variable

Una partícula de masa 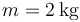$m=2\,\mathrm{kg}$ describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en $t=0\,\mathrm{s}$ del reposo en $x = 0$ .

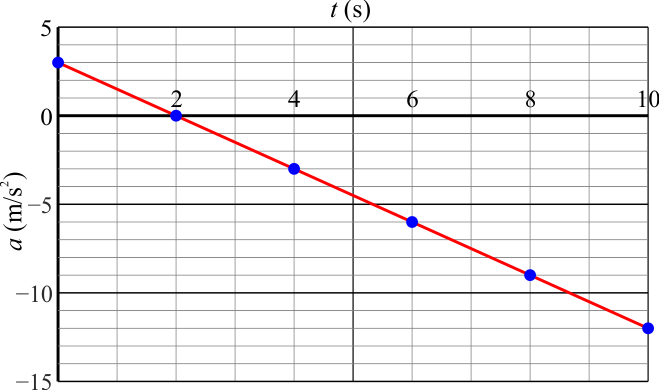
17.1 Pregunta 1

¿Cuánto vale la rapidez de la partícula en $t = 10\,\mathrm{s}$ ?

A 45 m/s
B -45 m/s
C No hay información suficiente para saberlo
D 51 m/s

Solución

La respuesta correcta es la A.

La aceleración representada en esta gráfica es lineal en thinsp

$a=A + B t\,$

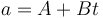
con las condiciones de que en t = 2 s se anula y en t = 0 s vale 3 m/s². Por tanto los coeficientes valen, en el SI,

$A=3\qquad\qquad B=-\frac{3}{2}$

siendo la aceleración

$a = 3-\frac{3}{2}t$

Integrando una vez hallamos la velocidad, sabiendo que la velocidad inicial es nula.

$v = \int_0^t a\,\mathrm{d}t=3t-\frac{3}{4}t^2$

En t = 10 s, esta velocidad vale

$v = 30-\frac{300}{4}=-45$

Puesto que la rapidez es el valor absoluto de la velocidad

$|v| = +45\,\frac{\mathrm{m}}{\mathrm{s}}$

17.2 Pregunta 2

¿Cuál es su velocidad media entre $t=0\,\mathrm{s}$ y $t=10\,\mathrm{s}$ ?

A −3.75 m/s
B −10 m/s
C −22.5 m/s
D −60 m/s

Solución

La respuesta correcta es la B.

Una vez que tenemos la velocidad hallamos la posición, sabiendo que parte de x = 0.

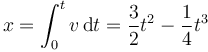
$x = \int_0^t v\,\mathrm{d}t=\frac{3}{2}t^2-\frac{1}{4}t^3$

La posición en t = 10 s es

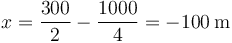
$x=\frac{300}{2}-\frac{1000}{4}=-100\,\mathrm{m}$

por lo que la velocidad media en este intervalo de tiempo es

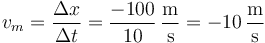
$v_m=\frac{\Delta x}{\Delta t}=\frac{-100}{10}\,\frac{\mathrm{m}}{\mathrm{s}}=-10\,\frac{\mathrm{m}}{\mathrm{s}}$

17.3 Pregunta 3

¿En qué instante(s) del intervalo 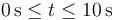$0\,\mathrm{s}\leq t \leq 10\,\mathrm{s}$ es nula la potencia desarrollada sobre la partícula?

A Solo en $t=2\,\mathrm{s}$ .
B Solo en $t=0\,\mathrm{s}$ y en $t=2\,\mathrm{s}$ .
C Solo en $t=0\,\mathrm{s}$ .
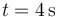
D En $t=0\,\mathrm{s}$ , en $t=2\,\mathrm{s}$ y $t=4\,\mathrm{s}$

Solución

La respuesta correcta es la D.

La potencia desarrollada sobre una partícula es igual al producto escalar de la fuerza por la velocidad. En un movimiento rectilíneo

$P=Fv =mav\,$

Por tanto se anula cuando se anule la aceleración o la velocidad.

La aceleración se anula, como muestra la gráfica, en t = 2 s.

La velocidad se anula en

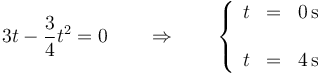
$3t-\frac{3}{4}t^2=0\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}t & = & 0\,\mathrm{s} \\ && \\ t & = & 4\,\mathrm{s}\end{array}\right.$

Por tanto la potencia se anula en t = 0 s, t = 2 s y t = 4 s.

17.4 Pregunta 4

¿Cuál es la distancia total recorrida $t=0\,\mathrm{s}$ y $t=10\,\mathrm{s}$ ?

A −600 m
B −100 m
C 100 m
D 116 m

Solución

La respuesta correcta es la D.

La distancia recorrida no coincide con el desplazamiento porque la velocidad cambia de signo.

El cambio de signo se produce cuando la velocidad se anula que, como se ve en la pregunta anterior, ocurre en t = 4 s.

El desplazamiento entre t = 0 s y t = 4 s es

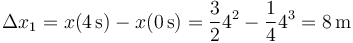
$\Delta x_1 = x(4\,\mathrm{s})-x(0\,\mathrm{s})=\frac{3}{2}4^2-\frac{1}{4}4^3 = 8\,\mathrm{m}$

y entre t = 4 s y t = 10 s

$\Delta x_2 = x(10\,\mathrm{s})-x(4\,\mathrm{s})=-100-8 = -108\,\mathrm{m}$

Por tanto la distancia total recorrida vale

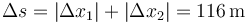
$\Delta s = |\Delta x_1|+|\Delta x_2| = 116\,\mathrm{m}$

18 Velocidad variable

Una partícula describe un movimiento rectilíneo en el que parte del reposo con velocidad inicial $v 0$ y su aceleración varía con el tiempo como

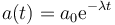
$a(t)=a_0\mathrm{e}^{-\lambda t}\,$

con $a 0$ y $λ$ constantes positivas.

¿Cómo cambia la velocidad de esta partícula con el tiempo?

A aumenta indefinidamente hasta infinito.
B disminuye indefinidamente hasta $-\infty$ .
C aumenta continuamente, tendiendo a un valor constante.
D disminuye gradualmente hasta cero.

Solución

La respuesta correcta es la C.

La aceleración, derivada de la velocidad, es siempre positiva. Por tanto la velocidad es una función creciente.

Por otro lado, al ser la aceleración una función que decae exponencialmente, su integral es finita, por lo que la velocidad no crece sin límite, sino que tiende a un valor constante

$v(t) = v_0+\int_0^t a_0\mathrm{e}^{-\lambda t}\mathrm{d}t=v_0+\frac{a_0}{\lambda}\left(1-\mathrm{e}^{-\lambda t}\right)\to v_0+\frac{a_0}{\lambda}$

19 Velocidad media

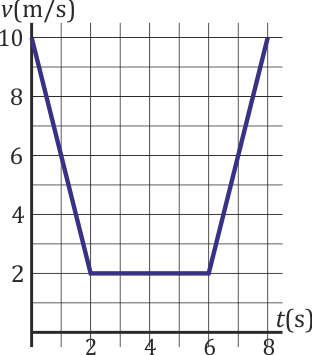
En un movimiento rectilíneo, la velocidad de una partícula como función del tiempo sigue la gráfica de la figura. ¿Cuánto vale la velocidad media en este intervalo de tiempo?

A 6 m/s
B 5 m/s
C 4 m/s
D 10 m/s

Solución

La respuesta correcta es la C.

Hallamos el desplazamiento como el área bajo la curva, que es la suma de tres trapecios (o de un rectángulo y dos triángulos)

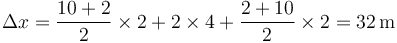
$\Delta x = \frac{10+2}{2}\times 2+2\times 4+\frac{2+10}{2}\times 2 = 32\,\mathrm{m}$

y queda la velocidad media

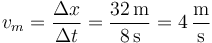
$v_m = \frac{\Delta x}{\Delta t}=\frac{32\,\mathrm{m}}{8\,\mathrm{s}}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

20 Caso de m.a.s.

En un movimiento armónico simple de frecuencia 3 rad/s la amplitud compleja o fasor de la velocidad es 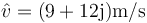$\hat{v}=(9+12\mathrm{j})\mathrm{m}/\mathrm{s}$ .

20.1 Pregunta 1

¿Cuanto vale la velocidad inicial de la partícula?

A 3 m/s
B 9 m/s
C 4 m/s
D 36 m/s

Solución

La respuesta correcta es la B.

El fasor de la elongación es el número complejo

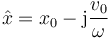
$\hat{x}=x_0-\mathrm{j}\frac{v_0}{\omega}$

y por tanto el de la velocidad

$\hat{v}=\mathrm{j}\omega\hat{x}=v_0+\mathrm{j}\omega x_0$

Igualando esta expresión a la del enunciado queda

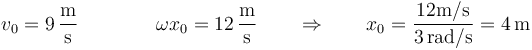
$v_0=9\,\frac{\mathrm{m}}{\mathrm{s}} \qquad\qquad \omega x_0=12\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\Rightarrow\qquad x_0=\frac{12\mathrm{m}/\mathrm{s}}{3\,\mathrm{rad}/\mathrm{s}}=4\,\mathrm{m}$

por lo que la velocidad inicial es 9m/s.

20.2 Pregunta 2

Para este movimiento, ¿cuánto vale la amplitud de las oscilaciones?

A 5 m
B 15 m
C 3 m
D 4 m

Solución

La respuesta correcta es la A.

La amplitud de las oscilaciones en un m.a.s. se puede calcular a partir de las condiciones iniciales como

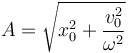
$A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$

que sustituyendo los valores de la pregunta anterior da

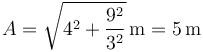
$A=\sqrt{4^2+\frac{9^2}{3^2}}\,\mathrm{m}=5\,\mathrm{m}$

21 Velocidad media

Una partícula se mueve a lo largo del eje OX con la velocidad instantánea $v (t) = B t 2$ Si $V$ es la velocidad instantánea en $t = T$ , y $v m$ es la velocidad media entre $t = 0$ y $t = T$ se cumple

A $v m = V / 2$ .
B $v m = V / 3$ .
C $v m = V$ .
D $v m = 2 V / 3$ .

Solución

La respuesta correcta es la B.

22 Velocidad inversamente proporcional a la posición

En un movimiento rectilíneo, la velocidad de una partícula sigue la ley como función de la posición $v = K / x$ . Inicialmente se encuentra en $x 0$ . ¿Qué ley sigue la posición como función del tiempo?

A $x (t) = (K / x 0) t + x 0$
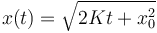
B $x(t)=\sqrt{2Kt+x_0^2}$
C $x (t) = x 0$
D $x (t) = x 0 - (K / x 0) t$

Solución

La respuesta correcta es la B.

Preguntas de test de cinemática del movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Identificación de movimiento

2 Movimiento definido a trozos

2.1 Pregunta 1

2.2 Pregunta 2

2.3 Pregunta 3

3 Cálculo de velocidad media

4 Propiedades de un m.a.s.

4.1 Pregunta 1

4.2 Pregunta 2

5 Movimiento con dependencia exponencial

6 Gráfica de una aceleración

6.1 Pregunta 1

6.2 Pregunta 2

6.3 Pregunta 3

7 Estudio de un m.a.s.

7.1 Pregunta 1

7.2 Pregunta 2

7.3 Pregunta 3

8 Velocidad cuadrática con la posición

8.1 Pregunta 1

8.2 Pregunta 2

8.3 Pregunta 3

9 Fasor de un movimiento armónico

10 Caso de movimiento armónico simple

10.1 Pregunta 1

10.2 Pregunta 2

11 Movimiento conocida la velocidad

11.1 Pregunta 1

11.2 Pregunta 2

12 Velocidad a partir de fasor

13 Caso de m.a.s.

13.1 Pregunta 1

13.2 Pregunta 2

14 Viaje en dos fases

15 Aceleración definida a trozos

15.1 Pregunta 1

15.2 Pregunta 2

16 Cálculo de fasor

17 Partícula con aceleración variable

17.1 Pregunta 1

17.2 Pregunta 2

17.3 Pregunta 3

17.4 Pregunta 4

18 Velocidad variable

19 Velocidad media

20 Caso de m.a.s.

20.1 Pregunta 1

20.2 Pregunta 2

21 Velocidad media

22 Velocidad inversamente proporcional a la posición

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES