Problemas de corriente eléctrica (GIE)
De Laplace
1 Problemas de boletín
1.1 Velocidad de arrastre en un hilo de plata
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
1.2 Cable bimetálico
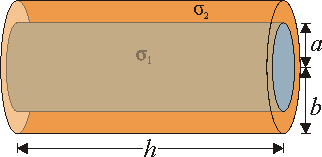
Entre los distintos tipos de cable empleados en la industria, se encuentra el de acero revestido de cobre. Está formado por un núcleo de acero de radio a (suponga 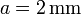 ), rodeado por una capa de cobre, de radio exterior b (sea
), rodeado por una capa de cobre, de radio exterior b (sea 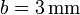 ).
).
- Calcule la resistencia de un cable de esta clase de longitud
 .
.
- Determine la intensidad de corriente que circula por cada metal cuando se aplica una diferencia de potencial
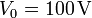 al cable anterior.
al cable anterior.
Datos: 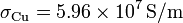 ,
, 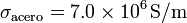
1.3 Paso de un pulso de corriente
Por un hilo rectilíneo de gran longitud y resistencia eléctrica R1 circula una corriente variable en el tiempo, tal que su valor es
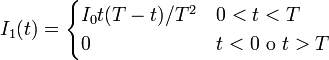
- Halle la carga que pasa por un punto del hilo entre
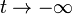 y
y 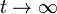 .
.
- Calcule la energía disipada en el cable en el mismo tiempo.
1.4 Asociación de dos bombillas en serie
Se colocan en serie dos bombillas de potencias nominales 10 W y 6 W y se conectan a la red. Si la potencia radiada es proporcional a la potencia consumida, ¿cuál de las dos bombillas darán más luz? ¿En qué proporción?
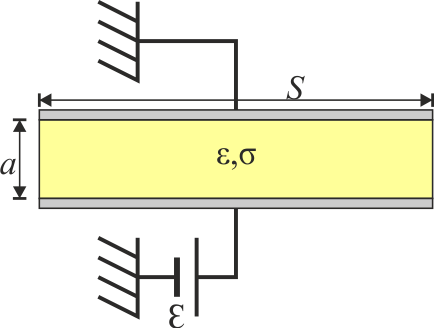
1.5 Condensador con pérdidas
En un modelo de condensador real (“con pérdidas”) se tienen dos placas paralelas perfectamente conductoras de sección S, separadas una distancia a entre las cuales hay un dieléctrico de permitividad  y con una pequeña conductividad σ. Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m
y con una pequeña conductividad σ. Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m 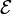 .
.
- Calcule el campo eléctrico y la densidad de corriente entre las placas.
- Halle la energía almacenada en el sistema y la potencia consumida en el dispositivo.
- Diseñe el circuito equivalente a este dispositivo.
- Si la fuente que alimenta a este elemento es una fuente real con f.e.m.
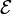 y resistencia interna r, ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
y resistencia interna r, ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
- Si la d.d.p. que se aplica entre las placas no es continua, sino que varía como V(t), ¿qué corriente llega por el cable al dispositivo?
- ¿Qué ocurre si se desconecta la fuente?
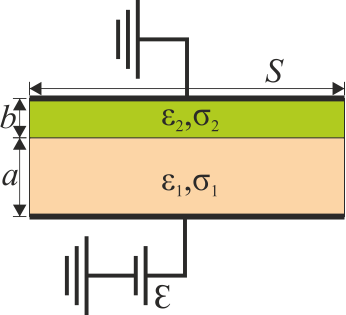
1.6 Condensador con dos capas no ideales
Entre dos placas perfectamente conductoras de sección S separadas una distancia a + b se encuentran dos capas de dieléctricos no ideales de espesores a y b respectivamente. Los dieléctricos tienen permitividades 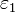 y
y 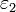 y conductividades σ1 y σ2, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m.
y conductividades σ1 y σ2, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m. 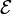 .
.
- Diseñe el circuito equivalente a este sistema.
- Calcule la corriente que atraviesa el dispositivo.
- Halle la carga en cada una de las placas y en la interfaz central entre los dos dieléctricos.
- Calcule la potencia disipada y la energía almacenada en el sistema.
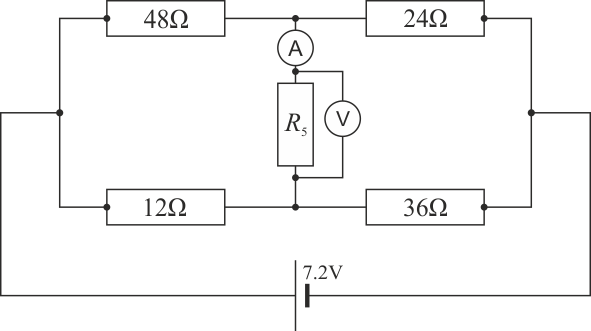
1.7 Sistema de 5 resistencias
Se tiene el sistema de 5 resistencias de la figura. Entre los extremos de la asociación se aplica una diferencia de potencial de 7.2 V.
Determine las lecturas del amperímetro y voltímetro de la rama central en los casos:
-
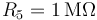
-
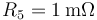
-
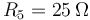
- El valor de R5 que haga máxima la potencia disipada en ella por efecto Joule.
1.8 Esfera que se conecta a una fuente de tensión
Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga 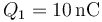 . Alrededor de la esfera no hay más conductores ni cargas.
. Alrededor de la esfera no hay más conductores ni cargas.
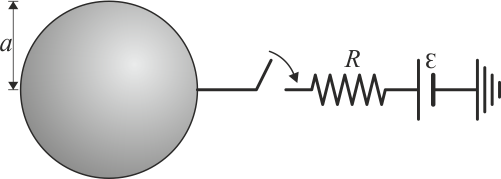
- Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
- Suponga que ahora se conecta a la esfera una fuente de tensión de 0.3 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
- Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
- ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
- Determine la ecuación diferencial que gobierna el potencial V(t) de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de V(t) frente al tiempo.
Dato: 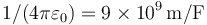
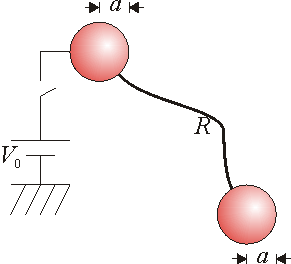
1.9 Dos esferas conectadas por una resistencia
Dos esferas metálicas, perfectamente conductoras, de radio a, se encuentran muy alejadas la una de la otra (de forma que no se influyen entre sí). Las dos esferas se encuentran conectadas mediante un cable de resistencia R. Una de las esferas se encuentra conectada a un generador de tensión V_0, a través de un interruptor que inicialmente se encuentra abierto. Ambas esferas están inicialmente descargadas.
- Suponga que el interruptor se cierra durante un periodo de tiempo muy corto (el imprescindible para que se cargue la esfera conectada a él) y se vuelve a abrir. Justo tras este intervalo ¿cómo es la distribución de cargas y potenciales en las esferas? ¿Cuánto vale la energía electrostática almacenada en el sistema?
- Si se deja transcurrir un periodo de tiempo largo, ¿cómo queda la distribución de cargas y potenciales? ¿Cuál es la energía electrostática almacenada en el sistema en el estado final?
- Determine la evolución en el tiempo de las cargas y potenciales en cada esfera, así como la corriente que circula por el cable.
- Halle la energía disipada en el cable durante el periodo transitorio y verifique que se satisface el balance energético.
- Suponga ahora que, en el proceso anterior, el generador no se desconecta, sino que se deja permanentemente conectado a la primera esfera. En ese caso, ¿cómo varía la carga en cada esfera? ¿Y la corriente por el cable? ¿Y la energía disipada y la energía almacenada?
2 Problemas adicionales
2.1 Resistividad dependiente de la posición
Tras una rotura de un cable de cobre (de resistividad r1) de sección S y gran longitud, se procede a unir los dos pedazos mediante una soldadura. Como consecuencia de la presencia de óxido la resistividad del cable aumenta hasta un valor r2 en una región alrededor del punto de contacto, pudiéndose describir matemáticamente según la ley
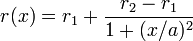
Calcule el aumento de la resistencia total del cable. Aplíquese al caso  ,
, 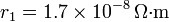 ,
, 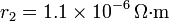 ,
, 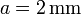 .
.
2.2 Conexiones de dos bombillas
Se desea encender dos bombillas de resistencia R0, para lo cual se dispone de una batería de f.e.m. 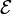 y resistencia interna r.
y resistencia interna r.
- En un primer montaje se disponen las dos bombillas en serie.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen (que dará una medida de la luz que desprenden).
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- A continuación se prueba a montarlas en paralelo.
- Calcule la intensidad de corriente que circula por cada una.
- Halle la potencia que consumen.
- Calcule la potencia desarrollada por el generador y el consumo de energía en el propio generador.
- ¿En cuál de los dos montajes el conjunto de las dos bombillas dará más luz?
- Supongamos que tenemos una batería de 10 V y 1 Ω de resistencia interna y dos bombillas en cuya etiqueta pone “10V 25W”, ¿cómo deberemos montarlas para que den el máximo de luz? ¿Cuánta potencia consumirán en ese caso?
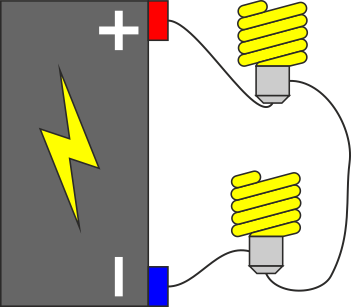

2.3 Conexiones de cuatro bombillas
Se dispone de cuatro bombillas, A, B, C, D. El etiquetado de estas bombillas indica que, para un voltaje de 120V, sus potencias nominales son respectivamente 30W, 60W, 120W y 40W. Se montas la cuatro bombillas en el siguiente esquema y se aplica entre los extremos una diferencia de potencial de 120V.
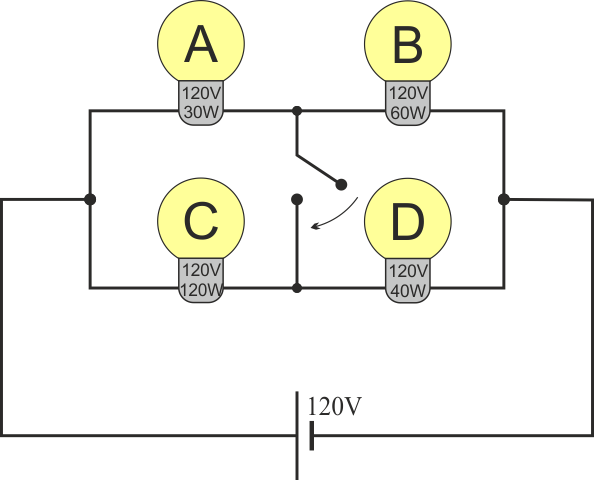
- Calcule el consumo de cada bombilla (en vatios) para este montaje, así como el consumo total del montaje. ¿Cuál es la que da más luz? ¿Y la que menos?
- Suponga que se cierra el interruptor central. Una vez cerrado, ¿cuál es el nuevo consumo total y el individual? ¿Cuál es ahora la bombilla más brillante y la menos brillante?
3 Preguntas de test
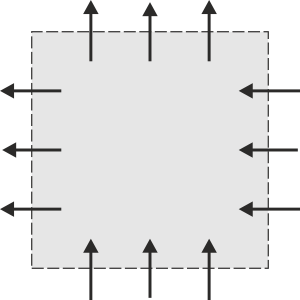
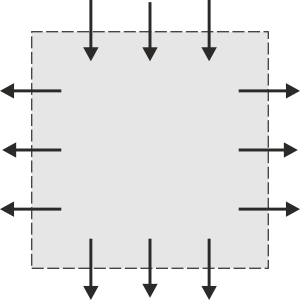
3.1 Flujo a través de una superficie cerrada
Indique en cuál de los cuatro casos siguientes, la superficie S delimitada por la línea discontinua encierra una carga que está aumentando. Las flechas representan el sentido de la densidad de corriente.
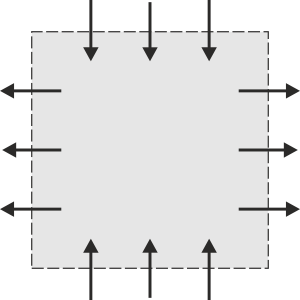
| 
|
| A | B |
|---|---|

| 
|
| C | D |
3.2 Conexión de dos hilos
Se tienen dos hilos de 1 mm de diámetro y 1 m de longitud, uno de ellos de cobre (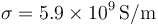 ) y el otro de aluminio (
) y el otro de aluminio (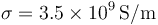 )
)
Si los dos hilos se conectan en paralelo y se aplica una diferencia de potencial a la asociación, ¿cuál de las siguientes afirmaciones es cierta?
- A La densidad de corriente es mayor en el cobre.
- B La densidad de corriente es mayor en el aluminio.
- C El campo eléctrico es mayor en el cobre.
- D La intensidad de corriente es la misma en los dos materiales.
Si los dos hilos se conectan en serie y se aplica una diferencia de potencial a la asociación, ¿cuál de las siguientes afirmaciones es cierta?
- A La densidad de corriente es mayor en el aluminio.
- B El campo eléctrico es mayor en el cobre.
- C La densidad de corriente es mayor en el cobre.
- D La intensidad de corriente es la misma en los dos materiales.
3.3 Sistema de tres resistencias
Dado el sistema de tres resistencias de la figura,
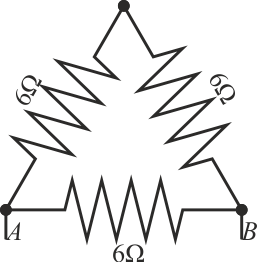
¿cuánto vale la resistencia equivalente entre A y B?
- A 9 Ω.
- B 18 Ω.
- C 2 Ω.
- D 4 Ω.
3.4 Circuito con tres resistencias
Se tiene el circuito de la figura.
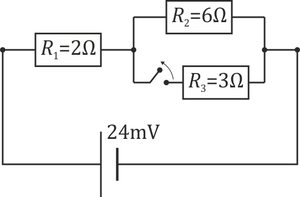
En un momento dado, se abre el interruptor. Después de ese momento, ¿qué podemos decir de las corrientes que circulan por las resistencias 1 y 2?
- A Las dos disminuyen.
- B La que pasa por la 1 se queda igual y la de la 2 aumenta.
- C La que pasa por la 1 disminuye y la de la 2 aumenta.
- D Las dos aumentan.
3.5 Fuente real conectada a dos resistencias
Una fuente de tensión con una f.e.m. de 9.0 V y 1 Ω de resistencia interna se conecta a una asociación en paralelo de dos resistencias de 3 Ω y 6 Ω.
¿Cuánto vale la d.d.p. entre los polos de la fuente de tensión?
- A 8.1 V
- B 6.0 V
- C No hay información suficiente para saberlo.
- D 9.0 V
¿Cuánta potencia se disipa en la asociación en paralelo?
- A 7.3 W
- B 9 W
- C 81 W
- D 18 W
3.6 Tres resistencias
Se tiene la asociación de tres resistencias mostrada en la figura
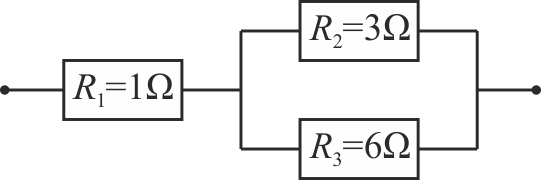
Si por la resistencia R1 circula una corriente 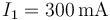 , ¿cuánto valen las corrientes por las otras dos?
, ¿cuánto valen las corrientes por las otras dos?
- A No hay información suficiente para determinarlas.
- B
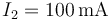 ,
, 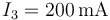
- C
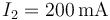 ,
, 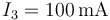
- D
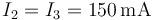
Si la diferencia de potencial entre los extremos de R1 es de 30 V, ¿cuánto valen las diferencias de potencial entre los extremos de las otras dos resistencias?
- A
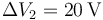 ,
, 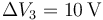
- B
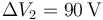 ,
, 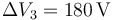
- C No hay información suficiente para determinarlas.
- D
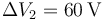 ,
, 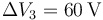
- A
3.7 Fusible
Un fusible es un fino hilo de plomo (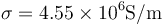 ) de 1 cm de largo y 0.2 mm de diámetro. Si el hilo se funde cuando la potencia disipada en él es de 25 mW, ¿Cuál es, aproximadamente, la máxima corriente que puede circular por este hilo?
) de 1 cm de largo y 0.2 mm de diámetro. Si el hilo se funde cuando la potencia disipada en él es de 25 mW, ¿Cuál es, aproximadamente, la máxima corriente que puede circular por este hilo?
- A 2.25 A
- B 0.6 A
- C 5.1 A
- D 62 mA
3.8 Fuente real conectada a R y C
Se construye un circuito formado por una fuente de tensión real de f.e.m. 9.0 V y resistencia interna 1.5 Ω conectada a la asociación en paralelo de una resistencia de 3.0 Ω y un condensador ideal de 100 nF
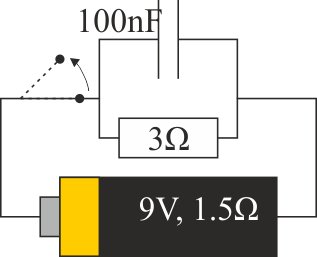
¿Qué potencia se disipa en la resistencia externa?
- A 243.0 W
- B 12.0 W
- C 18.0 W
- D 27.0 W
¿Cuánta energía hay almacenada en el condensador?
- A Ninguna, ya que está cortocircuitado.
- B 8.10 μJ.
- C 1.80 μJ.
- D 3.60 μJ.
Si en este circuito se abre bruscamente un interruptor, desconectando la fuente, ¿qué ocurre?
- A Fluye una corriente por el condensador, hasta que éste se descarga.
- B Deja inmediatamente de circular corriente por el circuito.
- C Fluye una corriente por la resistencia externa, hasta que se descarga el condensador.
- D Continúa fluyendo una corriente por el interior de la fuente.
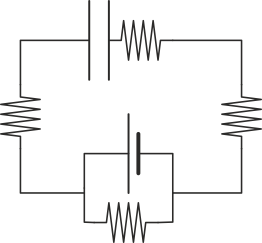
3.9 Circuito real
Un circuito real está formado por una pila, que se conecta por sendos cables a las placas de un condensador real, en cuyo interior hay un dieléctrico con permitividad y conductividad no nulas.
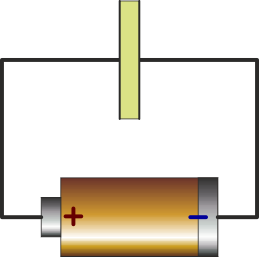
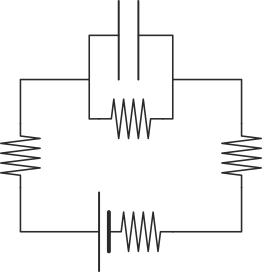
¿Cómo es el circuito equivalente de este sistema?

| 
|
| A | B |
|---|---|
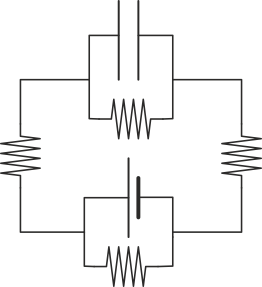
| 
|
| C | D |
3.10 Dos esferas alejadas
Se tienen un sistema de dos esferas conductoras (“1” y “2”) muy alejadas entre sí, de radios 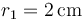 , y
, y 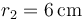 , respectivamente, que pueden unirse por un hilo conductor de 100 Ω. No hay más cargas ni conductores en el sistema. Inicialmente la esfera 1 almacena una carga de 20 nC y la esfera 2 una carga de 40 nC.
, respectivamente, que pueden unirse por un hilo conductor de 100 Ω. No hay más cargas ni conductores en el sistema. Inicialmente la esfera 1 almacena una carga de 20 nC y la esfera 2 una carga de 40 nC.
Una vez que se conectan por el hilo…
- A no fluye corriente alguna por el hilo.
- B no hay información suficiente para saber hacia dónde va la corriente.
- C fluye una intensidad de corriente que va de la esfera 1 a la 2.
- D fluye una intensidad de corriente que va de la esfera 2 a la 1.
Entre el estado inicial y el estado de equilibrio final, ¿cuánta energía se ha disipado en el hilo conductor?
- A 7.5 μJ
- B 210 μJ
- C 15 μJ
- D 202.5 μJ
3.11 Circuito con condensador y resistencias
Dado el circuito de la figura,
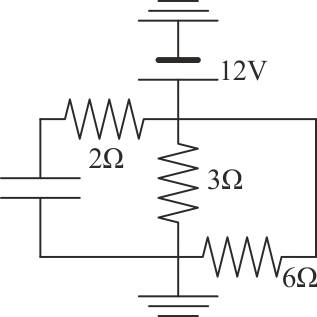
¿cuánto vale la corriente eléctrica que sale del generador?
- A 12 A
- B 4 A
- C 6 A
- D 1.09 A
¿Cuánto vale la diferencia de potencial entre las placas del condensador?
- A 0 V
- B 12 V
- C 4 V
- D No hay información suficiente para determinarla.
3.12 Dos hilos en paralelo
Un cable por el que circula una cierta corriente I0 se separa en dos hilos en paralelo del mismo material y la misma longitud, siendo el “1” de 3 mm de diámetro y el “2” de 1 mm de diámetro. ¿Cómo se reparte la corriente entre los dos hilos?
- A El 1 el 90% y el 2 el 10%.
- B El 1 el 25% y el 2 el 75%.
- C El 1 el 75% y el 2 el 25%.
- D El 1 el 50% y el 2 el 50%





