Dos esferas conectadas por una resistencia

De Laplace

Contenido

1 Enunciado

1 Enunciado

Dos esferas metálicas, perfectamente conductoras, de radio a, se encuentran muy alejadas la una de la otra (de forma que no se influyen entre sí). Las dos esferas se encuentran conectadas mediante un cable de resistencia R. Una de las esferas se encuentra conectada a un generador de tensión V_0, a través de un interruptor que inicialmente se encuentra abierto. Ambas esferas están inicialmente descargadas.

Suponga que el interruptor se cierra durante un periodo de tiempo muy corto (el imprescindible para que se cargue la esfera conectada a él) y se vuelve a abrir. Justo tras este intervalo ¿cómo es la distribución de cargas y potenciales en las esferas? ¿Cuánto vale la energía electrostática almacenada en el sistema?
Si se deja transcurrir un periodo de tiempo largo, ¿cómo queda la distribución de cargas y potenciales? ¿Cuál es la energía electrostática almacenada en el sistema en el estado final?
Determine la evolución en el tiempo de las cargas y potenciales en cada esfera, así como la corriente que circula por el cable.
Halle la energía disipada en el cable durante el periodo transitorio y verifique que se satisface el balance energético.
Suponga ahora que, en el proceso anterior, el generador no se desconecta, sino que se deja permanentemente conectado a la primera esfera. En ese caso, ¿cómo varía la carga en cada esfera? ¿Y la corriente por el cable? ¿Y la energía disipada y la energía almacenada?

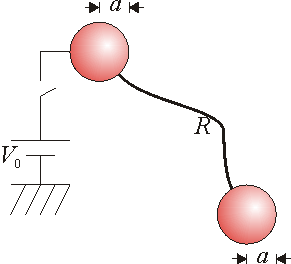
1.1 Estado inmediatamente posterior a la conexión

Cuando se cierra el interruptor, la esfera conectada a él, que llamaremos “1”, se coloca inmediatamente a tensión $V 0$ (estamos suponiendo que la conexión a la fuente se hace a través de un hilo ideal).

$V_{10} = V_0\qquad (t=0^+)$

Puesto que la segunda esfera se encuentra muy alejada, no produce influencia sobre la primera y la carga $Q 1$ puede hallarse como en el problema de una sola esfera.

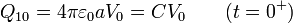
$Q_{10} = 4\pi\varepsilon_0 a V_0=CV_0\qquad (t=0^+)$

donde, por abreviar, llamamos C a la capacidad de una sola esfera 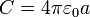$C=4\pi\varepsilon_0a$ .

La otra esfera (que llamaremos “2”), en cambio, no se ve afectada en el instante inicial. Como el cable que la conecta a la primera no es ideal, las crgas necesitan un cierto tiempo para viajar por él y acumularse en la esfera 2. Por ello

$Q_{20} = 0\qquad (t=0^+)$

y su tensión, al no verse afectada por la primera esfera, será también nula

$V_{20} = \frac{Q_{20}}{C} = 0\qquad (t=0^+)$

El que no haya carga en el instante inicial no quiere decir que la carga no comienza a acumularse desde el principio. Una vez que se establece la diferencia de potencial comienza a circular por el cable una corriente, que vale inicialmente

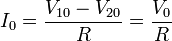
$I_{0}=\frac{V_{10}-V_{20}}{R}=\frac{V_0}{R}$

La energía almacenada en este instante inicial será

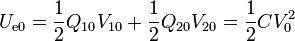
$U_{\mathrm{e}0}=\frac{1}{2}Q_{10}V_{10}+\frac{1}{2}Q_{20}V_{20}=\frac{1}{2}CV_0^2$

Si, tras este proceso de carga inicial se abre el interruptor muy rápidamente, el estado inicial no cambia, pero desde este momento la tensión de la esfera 1 deja de estar fijada. Tampoco su carga permanecerá constante, pues parte de ella se irá a la esfera 2.

1.2 Estado estacionario final

La presencia de una diferencia de potencial entre las esferas provoca la aparición de una corriente eléctrica por el cable. Esta corriente retira carga de la primera esfera y la almacena en la segunda.

El proceso se detiene cuando ambas esferas se encuentren al mismo potencial

$V_{1\infty}=V_{2\infty}\qquad(t\to\infty)$

La carga de cada esfera puede ser la misma o ser diferente. Lo único que sabemos es que la carga total del sistema no ha cambiado desde la apertura del interruptor, ya que no ha podido llegar ninguna desde fuera ni desparecer la que había. Por tanto

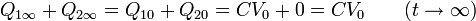
$Q_{1\infty}+Q_{2\infty}=Q_{10}+Q_{20}=CV_0+0=CV_0\qquad (t\to\infty)$

Ahora bien, puesto que las capacidades de las dos esferas son iguales, esta ecuación conduce a

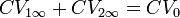
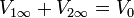
$CV_{1\infty}+CV_{2\infty}=CV_0\,$ $V_{1\infty}+V_{2\infty}=V_0\,$

que, junto con la igualdad de los potenciales nos da

$V_{1\infty}=V_{2\infty}=\frac{V_0}{2}$

y, para las cargas

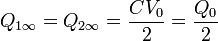
$Q_{1\infty}=Q_{2\infty}=\frac{CV_0}{2}=\frac{Q_0}{2}$

Luego efectivamente la carga se reparte mitad y mitad entre ambas esferas, pero esto es consecuencia de que ambas tienen la misma capacidad, por ser del mismo tamaño. Si fueran de distinto radio, la carga se distribuiría de forma diferente entre ellas.

Una vez alcanzado el equilibrio electrostático ya no hay corriente circulando por el cable

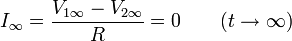
$I_{\infty}=\frac{V_{1\infty}-V_{2\infty}}{R}=0\qquad(t\to\infty)$

En cuanto a la energía final, es la mitad de la inicial

$U_{\mathrm{e}\infty}=\frac{1}{2}Q_{1\infty}V_{1\infty}+\frac{1}{2}Q_{2\infty}V_{2\infty} = \frac{1}{2}\left(\frac{CV_0}{2}\right)\left(\frac{V_0}{2}\right)+ \frac{1}{2}\left(\frac{CV_0}{2}\right)\left(\frac{V_0}{2}\right) = \frac{CV_0^2}{4}=\frac{U_{\mathrm{e}0}}{2}$

La diferencia en las energías se ha disipado, como veremos, por efecto Joule.

1.3 Evolución temporal

Entre el estado inicial y el final se produce en estado transitorio, en el que la esfera 1 se va descargando gradualmente, mientras que la 2 se va cargando.Se trata de ver cómo se produce esta evolución temporal.

En un instante $t$ los potencial de ambas esferas será $V 1 (t)$ y $V 2 (t)$ : Sus cargas en ese instante valdrán

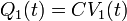
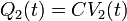
$Q_1(t)=CV_1(t)\,$ $Q_2(t)=CV_2(t)\,$

cumpliéndose en todo momento que

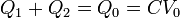
$Q_1 + Q_2 = Q_0 = CV_0\,$

La corriente que fluye de una esfera a la otra es

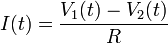
$I(t) = \frac{V_1(t)-V_2(t)}{R}$

y esta corriente coincidirá con la que sale de la esfera 1 (y entra en la 2)

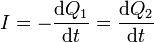
$I = -\frac{\mathrm{d}Q_1}{\mathrm{d}t}=\frac{\mathrm{d}Q_2}{\mathrm{d}t}$

Poniendo estas relaciones en función de los potenciales obtenemos, de la conservación de la carga total

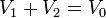
$V_1 + V_2 = V_0\,$

con lo que la corriente valdrá

$I = \frac{2V_1-V_0}{R}$

y la ley de conservación de la carga para la esfera 1

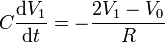
$C\frac{\mathrm{d}V_1}{\mathrm{d}t}=-\frac{2V_1-V_0}{R}$

o, escribiendo esto en forma de ecuación diferencial

$\frac{\mathrm{d}V_1}{\mathrm{d}t}+\frac{2}{RC}V_1=\frac{V_0}{RC}$

Esta es una ecuación de coeficientes constantes no homogénea. Su solución será la suma de una solución particular más una de la homogénea.

La solución particular ya la conocemos: es el estado final

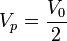
$V_p = \frac{V_0}{2}$

La solución de la homogénea cumple

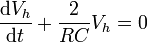
$\frac{\mathrm{d}V_h}{\mathrm{d}t}+\frac{2}{RC}V_h=0$ $\Rightarrow$ $V_h = A\mathrm{e}^{-t/\tau}\qquad \tau=\frac{RC}{2}$

y la solución de la ecuación completa será

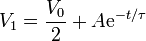
$V_1 = \frac{V_0}{2}+A\mathrm{e}^{-t/\tau}$

La constante $A$ la obtenemos de la condición inicial

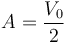
$V_0 = V_1(0) = \frac{V_0}{2}+A$ $\Rightarrow$ $A = \frac{V_0}{2}$

Por tanto las tensiones de las dos esferas varían como

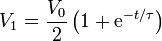
$V_1 = \frac{V_0}{2}\left(1+\mathrm{e}^{-t/\tau}\right)$ $V_2 = \frac{V_0}{2}\left(1-\mathrm{e}^{-t/\tau}\right)$

las cargas variarán de la misma forma

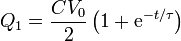
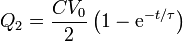
$Q_1 = \frac{CV_0}{2}\left(1+\mathrm{e}^{-t/\tau}\right)$ $Q_2 = \frac{CV_0}{2}\left(1-\mathrm{e}^{-t/\tau}\right)$

mientras que la corriente decae exponencialmente

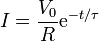
$I = \frac{V_0}{R}\mathrm{e}^{-t/\tau}$

1.4 Balance energético

Según hemos visto la energía inicial es

$U_{\mathrm{e}0}=\frac{CV_0^2}{2}$

y la final

$U_{\mathrm{e}\infty}=\frac{CV_0^2}{4}$

La pérdida de energía en el transitorio es

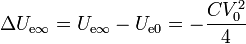
$\Delta U_{\mathrm{e}\infty}=U_{\mathrm{e}\infty}-U_{\mathrm{e}0}=-\frac{CV_0^2}{4}$

Veamos que esta energía se ha disipado por efecto Joule.

La potencia instantánea que se disipa en el cable es

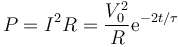
$P = I^2 R = \frac{V_0^2}{R} \mathrm{e}^{-2t/\tau}$

y la energía total disipada

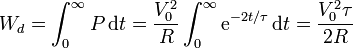
$W_d = \int_0^\infty P\,\mathrm{d}t = \frac{V_0^2}{R}\int_0^\infty \mathrm{e}^{-2t/\tau}\,\mathrm{d}t = \frac{V_0^2\tau}{2R}$

Sustituyendo el valor del tiempo de relajación

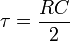
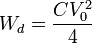
$\tau = \frac{RC}{2}$ $\Rightarrow$ $W_d = \frac{CV_0^2}{4}$

y, por tanto, se verifica el balance energético

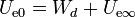
$U_{\mathrm{e}0} = W_d +U_{\mathrm{e}\infty}\,$

1.5 Caso de voltaje fijado

Si el interruptor no se vuelve a abrir sino que permanece cerrado en todo momento, pasamos de tener un proceso a carga (total) constante a uno de voltaje constante, pues la fuente fija en todo momento la tensión de la esfera 1. Ahora no se conservará la carga del sistema, pues la fuente puede aportar o retirar carga según las circunstancias.

1.5.1 Estado tras la conexión

El estado tras la conexión es el mismo que en el primer apartado, pues el proceso de carga inicial de la esfera 1 lo que hace es justamente poner su tensión a $V 0$ . Por tanto,

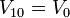
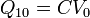
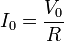
$V_{10}=V_0\,$ $Q_{10}=CV_0\,$ $Q_{20}=0\,$ $V_{20}=0\,$ $I_{0}=\frac{V_0}{R}$ $U_\mathrm{e0}=\frac{CV_0^2}{2}$

1.5.2 Estado final

La corriente que se genera por la diferencia de potencial retira carga de la esfera 1 y la lleva a la 2, pero, a diferencia del caso anterior, ahora la fuente repone la carga retirada, de forma que la tensión de la esfera 1 no cambia.

Por ello, cuando se alcanza el estado estacionario final, la tensión de ambas esferas es la misma e igual a $V 0$ , que es el valor constante para la esfera 1.

$V_{1\infty}=V_{2\infty}=V_0\qquad(t\to\infty)$

Las cargas finales serán ahora

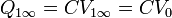
$Q_{1\infty}=CV_{1\infty}=CV_0\,$ $Q_{2\infty}=CV_{2\infty}=CV_0\qquad(t\to\infty)$

La corriente final será nula

$I_\infty = \frac{V_{1\infty}-V_{2\infty}}{R}=0$

y la energía final será ahora mayor que la inicial

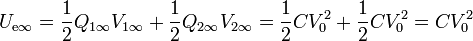
$U_{\mathrm{e}\infty}=\frac{1}{2}Q_{1\infty}V_{1\infty}+\frac{1}{2}Q_{2\infty}V_{2\infty}= \frac{1}{2}CV_0^2+\frac{1}{2}CV_0^2=CV_0^2$

1.5.3 Evolución

La variación temporal la obtenemos de que la corriente en cada instante vale

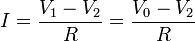
$I=\frac{V_1-V_2}{R}=\frac{V_0-V_2}{R}$

y esta corriente equivale a la carga que se almacena en la esfera 2 (pero no a la que sale de la esfera 1, pues en esta esfera hay un aporte de carga por el cable de la fuente).

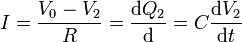
$I = \frac{V_0-V_2}{R} = \frac{\mathrm{d}Q_2}{\mathrm{d}}=C\frac{\mathrm{d}V_2}{\mathrm{d}t}$

o, en forma de ecuación diferencial

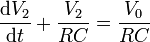
$\frac{\mathrm{d}V_2}{\mathrm{d}t}+\frac{V_2}{RC}=\frac{V_0}{RC}$

siendo la solución

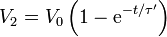
$V_2 = V_0\left(1-\mathrm{e}^{-t/\tau'}\right)$ $\tau'=RC\,$

Obsérvese que el nuevo tiempo de relajación es el doble que el anterior.

La carga de la segunda esfera aumenta proporcionalmente al potencial

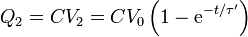
$Q_2=CV_2 = CV_0\left(1-\mathrm{e}^{-t/\tau'}\right)$

mientras que la corriente decae exponencialmente

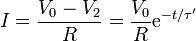
$I=\frac{V_0-V_2}{R} = \frac{V_0}{R}\mathrm{e}^{-t/\tau'}$

1.5.4 Balance energético

Según hemos dicho, en este proceso se produce un incremento en la energía almacenada

$\Delta U_{\mathrm{e}}=U_{\mathrm{e}\infty}-U_{\mathrm{e}0} = CV_0^2-\frac{1}{2}CV_0^2 = \frac{1}{2}CV_0^2$

pero la energía disipada por efecto Joule es naturalmente positiva

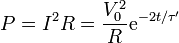
$P = I^2R = \frac{V_0^2}{R}\mathrm{e}^{-2t/\tau'}$ $W_d = \int_0^\infty P\,\mathrm{d}t = \frac{V_0^2\tau'}{2R} = \frac{CV_0^2}{2}$

Aunque ambas cantidades coinciden en su valor, juntas no explican el balance energético ya que la energía dispada está asociada a una disminución de la energía almacenada, no a un aumento de ella.

Para cuadrar las cuentas debemos incluir el trabajo realizado por el generador. Éste, al situar una cierta cantidad de carga a una tensión $V 0$ realiza un trabajo igual a la carga por el potencia

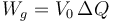
$W_g = V_0\,\Delta Q$

El incremento de carga es la diferencia entre la carga total del sistema en su estado final y la carga total inicial, ya que toda la carga tanto la de la esfera 1 como la de la 2 procede en última instancia de la fuente y aunque el potencial al que sitúa la carga en la esfera 2 no sea siempre $V 0$ , es a este valor al que la “sube” la fuente (aunque luego el potencial de esa carga caiga alo largo del cable).

Por tanto

$W_g = V_0(Q_{1\infty}+Q_{2\infty}-Q_{10}-Q_{20}) = V_0(CV_0+CV_0-CV_0-0) = CV_0^2$

y ahora sí cuadra el balance ya que

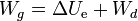
$W_g = \Delta U_\mathrm{e}+W_d\,$

esto es, durante el transitorio el generador aporta una cierta cantidad de energía, la mitad de la cual se disipa en forma de calor por efecto Joule y la otra mitad se queda almacenada.

Dos esferas conectadas por una resistencia

De Laplace

Contenido

1 Enunciado

1.1 Estado inmediatamente posterior a la conexión

1.2 Estado estacionario final

1.3 Evolución temporal

1.4 Balance energético

1.5 Caso de voltaje fijado

1.5.1 Estado tras la conexión

1.5.2 Estado final

1.5.3 Evolución

1.5.4 Balance energético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES