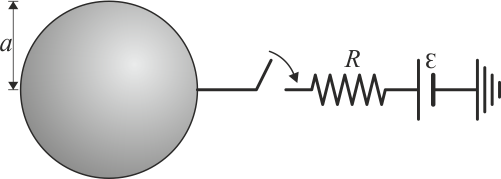
Esfera que se conecta a una fuente de tensión

De Laplace

Contenido

1 Enunciado
2 Estado inicial de la esfera
3 Corriente eléctrica
4 Estado final
5 Balance energético
6 Evolución del voltaje

1 Enunciado

Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga 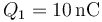$Q_1=10\,\mathrm{nC}$ . Alrededor de la esfera no hay más conductores ni cargas.

Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
Suponga que ahora se conecta a la esfera una fuente de tensión de 0.3 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
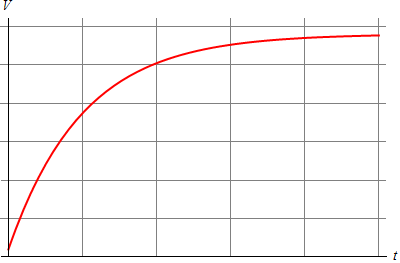
Determine la ecuación diferencial que gobierna el potencial $V (t)$ de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de $V (t)$ frente al tiempo.

Dato: 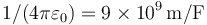$1/(4\pi\varepsilon_0) = 9\times 10^9\,\mathrm{m}/\mathrm{F}$

2 Estado inicial de la esfera

Cuando tenemos una esfera conductora de radio $a$ que almacena una carga $Q$ , el potencial de su superficie (y del interior también) es

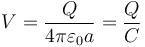
$V = \frac{Q}{4\pi\varepsilon_0a}=\frac{Q}{C}$

así que en este caso el potencial inicial de la esfera vale

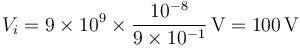
$V_i = 9\times 10^9\times\frac{10^{-8}}{9\times 10^{-1}}\,\mathrm{V}=100\,\mathrm{V}$

y la energía almacenada en el sistema es

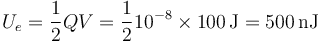
$U_e = \frac{1}{2}QV = \frac{1}{2}10^{-8}\times 100\,\mathrm{J}=500\,\mathrm{nJ}$

3 Corriente eléctrica

Una vez que se conecta la fuente, aparece una d.d.p. entre los extremos de la resistencia. Por un lado tenemos la esfera a 100 V y por otro la fuente a 300 V. La intensidad de corriente que circula por la resistencia en ese instante inicial es

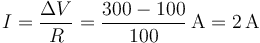
$I = \frac{\Delta V}{R}=\frac{300-100}{100}\,\mathrm{A}=2\,\mathrm{A}$

Nótese que es $I = Δ V / R$ , no $I = V / R$ .

Esta corriente va de mayor a menor voltaje, por tanto va hacia la esfera, y la carga de esta irá aumentando.

4 Estado final

El valor de la corriente calculado en el apartado anterior solo se aplica en el instante inicial. A medida que la esfera se va cargando se reduce la diferencia de potencial y la corriente va disminuyendo, hasta anularse. En ese momento se alcanza el nuevo equilibrio electrostático, en el que el voltaje es el mismo que el de la fuente, 0.3 kV. la carga en este estado final será, despejando en la fórmula del primer apartado,

$Q_f = CV_f=(4\pi\varepsilon_0 a)V_f = \frac{0.9\times 300}{9\times 10^9}\,\mathrm{C}=30\,\mathrm{nC}$

Lógicamente, si el voltaje se multiplica por 3, la carga almacenada también lo hace.

La nueva energía almacenada, será 3×3 = 9 veces mayor que antes

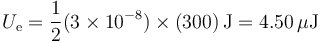
$U_\mathrm{e}=\frac{1}{2}(3\times 10^{-8})\times(300)\,\mathrm{J}=4.50\,\mu\mathrm{J}$

5 Balance energético

La fuente de tensión realiza un trabajo igual a la cantidad de carga que pasa por ella, multiplicada por la diferencia de potencial a la que la “sube”, que es de 0 V (tierra) a 0.3 kV. Por tanto su trabajo es

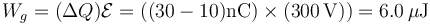
$W_g = (\Delta Q)\mathcal{E}=((30-10)\mathrm{nC})\times (300\,\mathrm{V}))= 6.0\,\mu\mathrm{J}$

Este trabajo realizado por el generador, parte se emplea en variar la energía almacenada y parte se escapa en forma de calor. La variación en la energía almacenada es

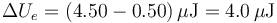
$\Delta U_e = (4.50-0.50)\,\mu\mathrm{J}= 4.0\,\mu\mathrm{J}$

así que la energía disipada vale

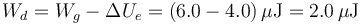
$W_d = W_g -\Delta U_e = (6.0-4.0)\,\mu\mathrm{J}=2.0\,\mu\mathrm{J}$

6 Evolución del voltaje

Obtenemos la ecuación a partir de la ley de conservación de la carga. Toda la corriente que llega a la esfera se emplea en aumentar su carga, ya que ésta no puede escapar por ningún sitio. Por tanto

$I(t) = \frac{\mathrm{d}Q}{\mathrm{d}t}$

La corriente que llega la obtenemos de la ley de Ohm

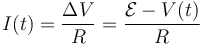
$I(t) = \frac{\Delta V}{R}=\frac{\mathcal{E}-V(t)}{R}$

y la carga almacenada en cada instante es proporcional al voltaje que tenga en ese momento

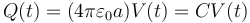
$Q(t) = (4\pi\varepsilon_0a)V(t) = C V(t)$

así que nos queda la ecuación diferencial

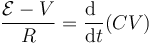
$\frac{\mathcal{E}-V}{R}=\frac{\mathrm{d}\ }{\mathrm{d}t}(CV)$

o, reordenando términos

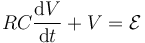
$RC\frac{\mathrm{d}V}{\mathrm{d}t}+ V = \mathcal{E}$

Esta es una ecuación diferencial de coeficientes constantes, cuya solución parte del estado inicial y tiende a un estado final asintóticamente, acercándose a él de forma exponencial. El tiempo típico para que se pueda decir que ha alcanzado el estado final es RC.

Esfera que se conecta a una fuente de tensión

De Laplace

Contenido

1 Enunciado

2 Estado inicial de la esfera

3 Corriente eléctrica

4 Estado final

5 Balance energético

6 Evolución del voltaje

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES