Condensador con dos capas no ideales

De Laplace

Contenido

1 Enunciado
2 Circuito equivalente
3 Corriente eléctrica
4 Cargas
5 Potencia y energía

1 Enunciado

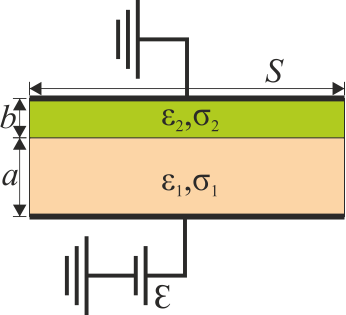
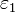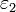Entre dos placas perfectamente conductoras de sección $S$ separadas una distancia $a + b$ se encuentran dos capas de dieléctricos no ideales de espesores $a$ y $b$ respectivamente. Los dieléctricos tienen permitividades $\varepsilon_1$ y $\varepsilon_2$ y conductividades $σ 1$ y $σ 2$ , respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m. 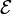$\mathcal{E}$ .

Diseñe el circuito equivalente a este sistema.
Calcule la corriente que atraviesa el dispositivo.
Halle la carga en cada una de las placas y en la interfaz central entre los dos dieléctricos.
Calcule la potencia disipada y la energía almacenada en el sistema.

2 Circuito equivalente

Al analizar el caso de un condensador real se llega a que equivale a la asociación en paralelo de un condensador ideal (sin resistencia) y de un resistor ideal (sin capacidad).

En este sistema de dos capas, la interfaz entre los dieléctricos es una equipotencial, ya que perpendicular al campo eléctrico, que va de una placa a la otra. Esto quiere decir que podemos separar el dispositivo como una asociación de dos condensadores reales.

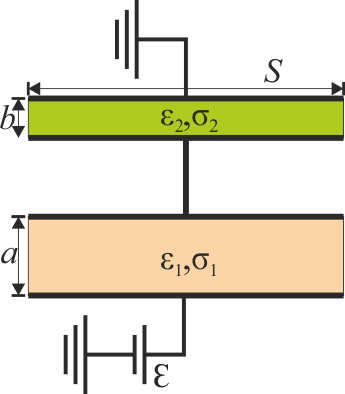
El circuito equivalente está formado entonces por la asociación en serie de dos asociaciones en paralelo, siendo las capacidades y resistencias respectivas

$C_1 = \frac{\varepsilon_1 S}{a}\qquad\qquad C_2 = \frac{\varepsilon_2 S}{b}\qquad\qquad R_1 = \frac{a}{\sigma_1 S}\qquad\qquad R_2 = \frac{b}{\sigma_2 S}$

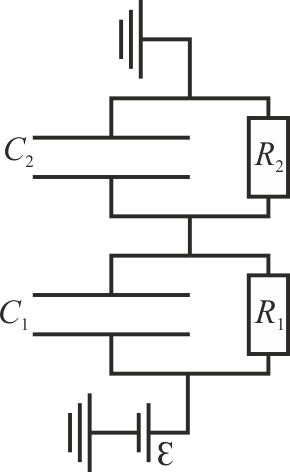
3 Corriente eléctrica

En corriente continua, no hay corriente por los condensadores, cuya carga permanece constante, por lo que la única corriente va por las resistencias. A su vez, la corriente que pasa por la primera resistencia debe pasar también por la segunda

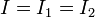
$I = I_1 = I_2\,$

y la diferencia de potencial total es la suma de la que cae en cada resistencia

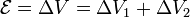
$\mathcal{E}=\Delta V = \Delta V_1 + \Delta V_2$

Por tanto, desde el punto de vista de la corriente, los condensadores no cuentan por ser ésta continua y el sistema equivale a dos resistencias en serie. La corriente que atraviesa ambas es

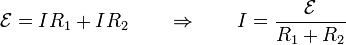
$\mathcal{E}= IR_1+IR_2 \qquad\Rightarrow\qquad I = \frac{\mathcal{E}}{R_1+R_2}$

siendo la diferencia de potencial en cada una

$\Delta V_1 = \frac{\mathcal{E}R_1}{R_1+R_2}\qquad\qquad \Delta V_2 = \frac{\mathcal{E}R_2}{R_1+R_2}$

En función de los datos del problema

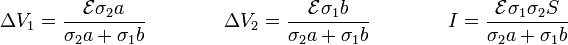
$\Delta V_1 = \frac{\mathcal{E}\sigma_2a}{\sigma_2 a+ \sigma_1 b}\qquad\qquad \Delta V_2 = \frac{\mathcal{E}\sigma_1b}{\sigma_2 a+ \sigma_1 b}\qquad\qquad I = \frac{\mathcal{E}\sigma_1\sigma_2S}{\sigma_2 a+ \sigma_1 b}$

En términos del dispositivo real de dos capas, lo que ocurre es que la corriente que parte de la placa positiva continúan sin detenerse hasta la placa negativa (y más allá, por el cable), por lo que necesariamente la intensidad de corriente que atraviesa el primer material es igual a la que atraviesa el segundo.

4 Cargas

Aunque haya corriente circulando por el sistema, los condensadores permanecen cargados, pues hay una diferencia de potencial entre sus placas. Desde el punto de vista de las cargas, el dispositivo no es equivalente a dos condensadores en serie, ya que la diferencia de potencial que debemos aplicar es la calculada en el apartado anterior. La carga en cada condensador será

$Q_1 = C_1\,\Delta V_1 = \frac{\mathcal{E}R_1C_1}{R_1+R_2}\qquad\qquad Q_2 = C_2\,\Delta V_2 = \frac{\mathcal{E}R_2C_2}{R_1+R_2}$

La carga en la placa inferior (conectada al polo positivo de la fuente, es igual a la carga del primer condensador

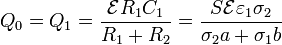
$Q_0 = Q_1 = \frac{\mathcal{E}R_1C_1}{R_1+R_2}= \frac{S\mathcal{E}\varepsilon_1\sigma_2}{\sigma_2a+\sigma_1b}$

La carga en la placa superior es la carga negativa del segundo condensador

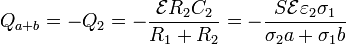
$Q_{a+b}=-Q_2 = -\frac{\mathcal{E}R_2C_2}{R_1+R_2}=-\frac{S\mathcal{E}\varepsilon_2\sigma_1}{\sigma_2a+\sigma_1b}$

En general estas dos cargas no son iguales y opuestas. ¿Quiere esto decir que tenemos un condensador en el que no se cumple la neutralidad del conjunto? No, ya que además existe una carga en la interfaz entre los dos dieléctricos, situada en $z = a$ . La carga neta en esta interfaz es la suma de la negativa del condensador 1 y la positiva del 2

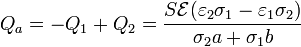
$Q_a = -Q_1+Q_2=\frac{S\mathcal{E}(\varepsilon_2\sigma_1-\varepsilon_1\sigma_2)}{\sigma_2a+\sigma_1b}$

¿De donde sale esta carga y dónde está almacenada? Se encuentra acumulada en la superficie de separación de los dos medios. Se acumuló en este punto durante el periodo transitorio inicial. Imaginemos que $σ 1 > σ 2$ , en ese caso, al conectarse la fuente, aparece una corriente más intensa en el material 1 que en el 2 En la interfaz, la carga procedente de la placa positiva por el medio 1 no es desalojada al mismo ritmo por el medio 2, con lo que se produce una acumulación de carga, que permanece en el estado estacionario.

Solo en el caso en que se cumpla

$R_1C_1 = R_2 C_2\qquad\mbox{o, equivalentemente}\qquad\frac{\varepsilon_1}{\sigma_1}=\frac{\varepsilon_2}{\sigma_2}\qquad\Rightarrow\qquad Q_a = 0$

5 Potencia y energía

Por el hecho de estar circulando una corriente por los materiales, se está disipando una energía en ellos

$P = I_1^2 R_1 +I_2^2 R_2 = I^2(R_1+R_2)=\frac{\mathcal{E}^2}{R_1+R_2}$

mientras permanece almacenada una cierta cantidad de energía

$U_\mathrm{e}=\frac{1}{2}C_1(\Delta V_1)^2+\frac{1}{2}C_2(\Delta V_2)^2=\frac{\mathcal{E}^2(C_1R_1^2+C_2R_2^2)}{2(R_1+R_2)^2}$

Condensador con dos capas no ideales

De Laplace

Contenido

1 Enunciado

2 Circuito equivalente

3 Corriente eléctrica

4 Cargas

5 Potencia y energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES