Resistividad dependiente de la posición

De Laplace

1 Enunciado

Tras una rotura de un cable de cobre (de resistividad

r 1

) de sección

S

y gran longitud, se procede a unir los dos pedazos mediante una soldadura. Como consecuencia de la presencia de óxido la resistividad del cable aumenta hasta un valor

r 2

en una región alrededor del punto de contacto, pudiéndose describir matemáticamente según la ley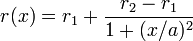 $r(x) = r_1 + \frac{r_2-r_1}{1+(x/a)^2}$

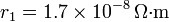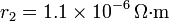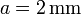Calcule el aumento de la resistencia total del cable. Aplíquese al caso $S=1\,\mathrm{mm}^2$ , $r_1= 1.7\times 10^{-8}\,\Omega{\cdot}\mathrm{m}$ , $r_2=1.1\times 10^{-6}\,\Omega{\cdot}\mathrm{m}$ , $a=2\,\mathrm{mm}$ .

2 Solución

La resistencia de un conductor filiforme tiene la expresión

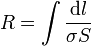
$R = \int \frac{\mathrm{d}l}{\sigma S}$

donde $d l$ es el diferencial de longitud a lo largo del cable, $σ$ su conductividad y $S$ la sección transversal. Estas dos cantidades pueden depender de la posición. Esta fórmula se puede leer como que la resistencia es la asociación en serie de infinitas resistencias diferenciales

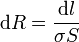
$\mathrm{d}R= \frac{\mathrm{d}l}{\sigma S}$

En este caso el diferencial de longitud es $d x$ y la sección es uniforme a lo largo del hilo. No así la conductividad.

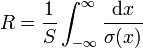
$R = \frac{1}{S}\int_{-\infty}^\infty \frac{\mathrm{d}x}{\sigma(x)}$

Si usamos la resistividad en vez de la conductividad la resistencia queda

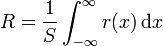
$R = \frac{1}{S}\int_{-\infty}^\infty r(x)\,\mathrm{d}x$

Esta integral da un resultado infinito (lo que es lógico, si consideramos un cable de longitud infinita), pero en realidad no se está preguntando por la resistencia total, sino por el incremento en la resistencia, esto es la diferencia con el valor que tendría si no hubiera soldadura:

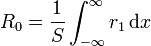
$R_0 = \frac{1}{S}\int_{-\infty}^\infty r_1\,\mathrm{d}x$

así que la cantidad buscada es

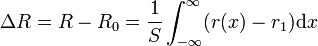
$\Delta R = R- R_0 = \frac{1}{S}\int_{-\infty}^\infty (r(x)-r_1)\mathrm{d}x$

Sustituyendo $r (x)$ e integrando esta cantidad obtenemos

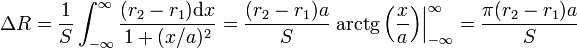
$\Delta R = \frac{1}{S}\int_{-\infty}^\infty \frac{(r_2-r_1) \mathrm{d}x}{1+(x/a)^2} = \frac{(r_2-r_1)a}{S}\left.\mathrm{arctg}\left(\frac{x}{a}\right)\right|_{-\infty}^\infty = \frac{\pi(r_2-r_1)a}{S}$

En el caso particular del enunciado, este aumento vale

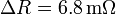
$\Delta R = 6.8\,\mathrm{m}\Omega$

lo que equivale a que el cable se comporta como si su longitud hubiera aumentado en 40 cm.

Resistividad dependiente de la posición

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES