Preguntas de test de corriente eléctrica (GIE)
De Laplace
1 Flujo a través de una superficie cerrada
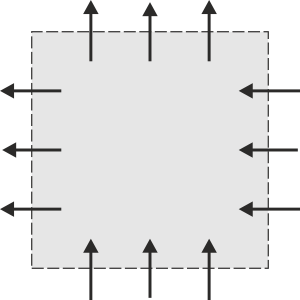
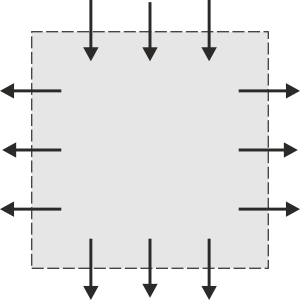
Indique en cuál de los cuatro casos siguientes, la superficie S delimitada por la línea discontinua encierra una carga que está aumentando. Las flechas representan el sentido de la densidad de corriente.
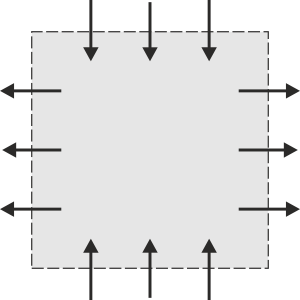
| 
|
| A | B |
|---|---|

| 
|
| C | D |
1.1 Solución
La respuesta correcta es la C.
La ley de conservación de la carga establece que
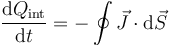
es decir, lo que aumenta la carga contenida en un volumen es igual a lo que fluye hacia el interior por la frontera de éste.
Examinando las cuatro figuras, vemos que en la figura C hay mayoría de líneas de corriente hacia el interior (3 caras a 1), cosa que no ocurre en el resto. Por tanto, es en ese caso en el que está aumentando la carga.
2 Conexión de dos hilos
Se tienen dos hilos de 1 mm de diámetro y 1 m de longitud, uno de ellos de cobre (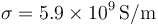 ) y el otro de aluminio (
) y el otro de aluminio (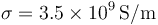 )
)
2.1 Pregunta 1
Si los dos hilos se conectan en paralelo y se aplica una diferencia de potencial a la asociación, ¿cuál de las siguientes afirmaciones es cierta?
- A La densidad de corriente es mayor en el cobre.
- B La densidad de corriente es mayor en el aluminio.
- C El campo eléctrico es mayor en el cobre.
- D La intensidad de corriente es la misma en los dos materiales.
2.1.1 Solución
La respuesta correcta es la A.
Si están en paralelo, la diferencia de potencial entre los extremos es la misma para ambos
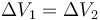
y si tienen la misma longitud también lo será el campo eléctrico (que es aproximadamente uniforme)
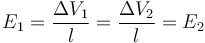
La densidad de corriente, en cambio es diferente

siendo la proporción entre ellas
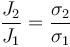
Por tanto la densidad de corriente es mayor donde la conductividad sea mayor, esto es, en el cobre.
2.2 Pregunta 2
Si los dos hilos se conectan en serie y se aplica una diferencia de potencial a la asociación, ¿cuál de las siguientes afirmaciones es cierta?
- A La densidad de corriente es mayor en el aluminio.
- B El campo eléctrico es mayor en el cobre.
- C La densidad de corriente es mayor en el cobre.
- D La intensidad de corriente es la misma en los dos materiales.
2.2.1 Solución
La respuesta correcta es la D.
Si están en serie, la cosa cambia. Ahora, lo que es igual en los dos cables es la intensidad de corriente que circula por ellos
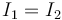
Con esto ya tenemos que la afirmación D es la correcta.
Para ver que el resto son falsas tenemos que, al ser de la misma sección, también coincide la densidad de corriente
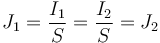
lo cual anula las respuestas A y C.
El campo eléctrico el que difiere entre los dos materiales

siendo su proporción
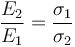
Esto implica que cuanto mayor es la conductividad menor es el campo. Por tanto en el cobre el campo es más débil, no más intenso.
3 Sistema de tres resistencias
Dado el sistema de tres resistencias de la figura,
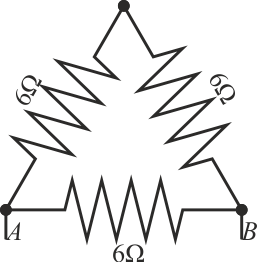
¿cuánto vale la resistencia equivalente entre A y B?
- A 9 Ω.
- B 18 Ω.
- C 2 Ω.
- D 4 Ω.
3.1 Solución
La respuesta correcta es la D.
Tenemos una asociación en paralelo de la resistencia de abajo con la asociación en serie de las dos de arriba.
La resistencia de la asociación en serie vale
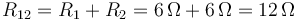
y para la asociación en paralelo se cumple
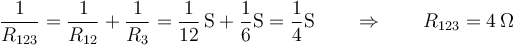
4 Circuito con tres resistencias
Se tiene el circuito de la figura.
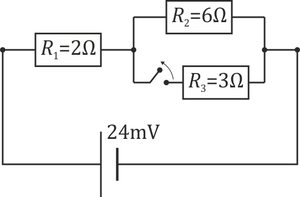
En un momento dado, se abre el interruptor. Después de ese momento, ¿qué podemos decir de las corrientes que circulan por las resistencias 1 y 2?
- A Las dos disminuyen.
- B La que pasa por la 1 se queda igual y la de la 2 aumenta.
- C La que pasa por la 1 disminuye y la de la 2 aumenta.
- D Las dos aumentan.
4.1 Solución
La respuesta correcta es la C.
Antes de abrir el interruptor, la resistencia equivalente al conjunto es
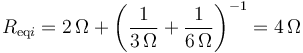
por lo que la corriente que circula por la resistencia 1 era
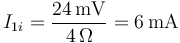
Esta corriente se repartía entre las dos ramas, en forma inversamente proporcional a la resistencia de cada una

Cuando se abre el interruptor deja de pasar corriente por R3, por lo que la nueva resistencia equivalente es
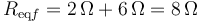
siendo la nueva corriente por la resistencia 1
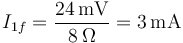
Vemos que ha disminuido como consecuencia de que ha aumentado la resistencia del circuito.
Esta misma corriente pasa por la resistencia 2, ya que ahora no se bifurca.
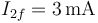
Por tanto, la corriente que va por la resistencia 1 disminuye y por la 2 aumenta.
5 Fuente real conectada a dos resistencias
Una fuente de tensión con una f.e.m. de 9.0 V y 1 Ω de resistencia interna se conecta a una asociación en paralelo de dos resistencias de 3 Ω y 6 Ω.
5.1 Pregunta 1
¿Cuánto vale la d.d.p. entre los polos de la fuente de tensión?
- A 8.1 V
- B 6.0 V
- C No hay información suficiente para saberlo.
- D 9.0 V
5.1.1 Solución
La respuesta correcta es la B.
La d.d.p. entre los polos de la fuente es igual a
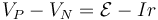
por lo que debemos calcular la corriente que circula por el circuito. Esta d.d.p. cumple también la ley de Ohm
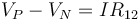
siendo R12 la resistencia correspondiente a la asociación en paralelo
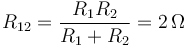
Igualando las dos d.d.p. y despejando
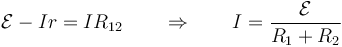
lo que nos da la corriente
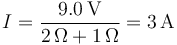
y por tanto la d.d.p. entre los bornes de la fuente vale
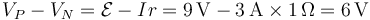
5.2 Pregunta 2
¿Cuánta potencia se disipa en la asociación en paralelo?
- A 7.3 W
- B 9 W
- C 81 W
- D 18 W
5.2.1 Solución
La respuesta correcta es la D.
La potencia disipada en la resistencia, de acuerdo con la ley de Joule, vale
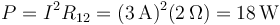
6 Tres resistencias
Se tiene la asociación de tres resistencias mostrada en la figura
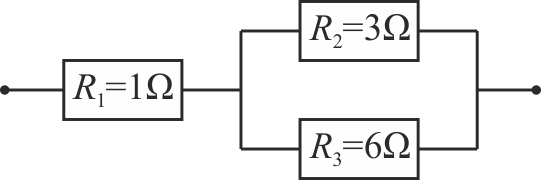
6.1 Pregunta 1
Si por la resistencia R1 circula una corriente 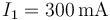 , ¿cuánto valen las corrientes por las otras dos?
, ¿cuánto valen las corrientes por las otras dos?
- A No hay información suficiente para determinarlas.
- B
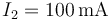 ,
, 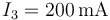
- C
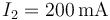 ,
, 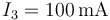
- D
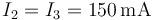
6.1.1 Solución
La respuesta correcta es la C.
La corriente que llega a la asociación en paralelo se separa en dos
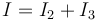
Por estar en paralelo la d.d.p. es la misma en las dos resistencias
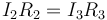
esto nos da un sistema de dos ecuaciones con dos incógnitas, con solución

que para este caso da

En general, en una asociación en paralelo, tenemos que la mayor parte de la corriente se va por el camino de menor resistencia, que en este caso es suficiente para determinar la respuesta correcta.
6.2 Pregunta 2
Si la diferencia de potencial entre los extremos de R1 es de 30 V, ¿cuánto valen las diferencias de potencial entre los extremos de las otras dos resistencias?
- A
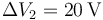 ,
, 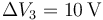
- B
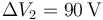 ,
, 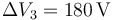
- C No hay información suficiente para determinarlas.
- D
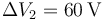 ,
, 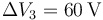
- A
6.2.1 Solución
La respuesta correcta es la D.
Si están en paralelo, la diferencia de potencial es la misma en las dos resistencias, por lo que la respuesta correcta es la D, o en todo caso la C, si la información no fuera suficiente.
Veamos que sí se puede determinar la d.d.p. Al conocer su valor para la primera resistencia, podemos calcular la corriente que circula por ella
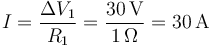
y ahora, como en la pregunta anterior, podemos hallar la corriente por cada una de las resistencias en paralelo

siendo la d.d.p. en cada una
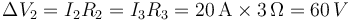
7 Fusible
Un fusible es un fino hilo de plomo (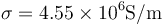 ) de 1 cm de largo y 0.2 mm de diámetro. Si el hilo se funde cuando la potencia disipada en él es de 25 mW, ¿Cuál es, aproximadamente, la máxima corriente que puede circular por este hilo?
) de 1 cm de largo y 0.2 mm de diámetro. Si el hilo se funde cuando la potencia disipada en él es de 25 mW, ¿Cuál es, aproximadamente, la máxima corriente que puede circular por este hilo?
- A 2.25 A
- B 0.6 A
- C 5.1 A
- D 62 mA
7.1 Solución
La respuesta correcta es la B.
La potencia disipada en la espira la da la ley de Joule
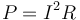
de donde la corriente máxima es igual a
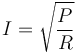
Aquí la resistencia es la de un hilo
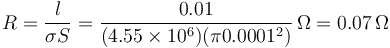
Por tanto
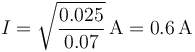
8 Fuente real conectada a R y C
Se construye un circuito formado por una fuente de tensión real de f.e.m. 9.0 V y resistencia interna 1.5 Ω conectada a la asociación en paralelo de una resistencia de 3.0 Ω y un condensador ideal de 100 nF
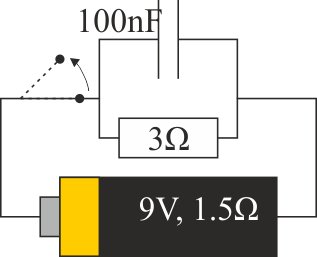
8.1 Pregunta 1
¿Qué potencia se disipa en la resistencia externa?
- A 243.0 W
- B 12.0 W
- C 18.0 W
- D 27.0 W
8.1.1 Solución
La respuesta correcta es la B.
En corriente continua, por el condensador no circula corriente, por lo que para calcular la corriente que recorre el circuito basta considerar la resistencia interna y la externa
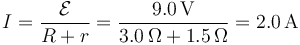
Por tanto la potencia disipada en la resistencia es
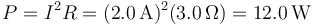
8.2 Pregunta 2
¿Cuánta energía hay almacenada en el condensador?
- A Ninguna, ya que está cortocircuitado.
- B 8.10 μJ.
- C 1.80 μJ.
- D 3.60 μJ.
8.2.1 Solución
La respuesta correcta es la C.
La energía almacenada en el condensador es
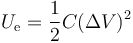
siendo la d.d.p. la misma que en la resistencia externa
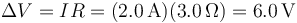
lo que da la energía
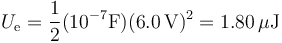
8.3 Pregunta 3
Si en este circuito se abre bruscamente un interruptor, desconectando la fuente, ¿qué ocurre?
- A Fluye una corriente por el condensador, hasta que éste se descarga.
- B Deja inmediatamente de circular corriente por el circuito.
- C Fluye una corriente por la resistencia externa, hasta que se descarga el condensador.
- D Continúa fluyendo una corriente por el interior de la fuente.
8.3.1 Solución
La respuesta correcta es la C.
Cuando se desconecta el circuito el generador deja de aportar corriente, pero inicialmente sigue existiendo una d.d.p. entre las placas del condensador (que está cargado) y por tanto una corriente por la resistencia externa.
la potencia disipada por esta corriente procede de la energía almacenada en el condensador, por lo que cuando este se descarga por completo deja de almacenar energía, ya no hay diferencia de potencial y desaparece la corriente por la resistencia.
9 Circuito real
Un circuito real está formado por una pila, que se conecta por sendos cables a las placas de un condensador real, en cuyo interior hay un dieléctrico con permitividad y conductividad no nulas.
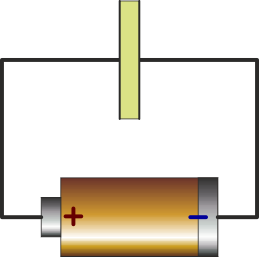
¿Cómo es el circuito equivalente de este sistema?

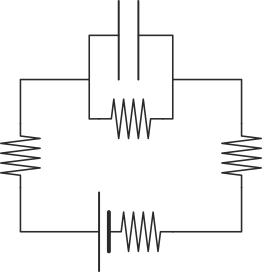
| 
|
| A | B |
|---|---|
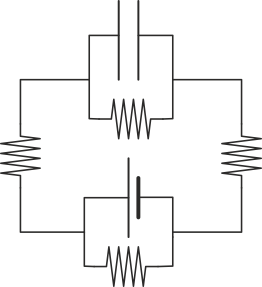
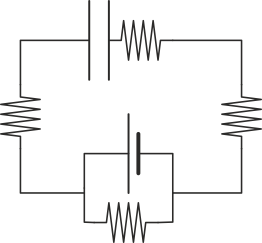
| 
|
| C | D |
9.1 Solución
La respuesta correcta es la B.
10 Dos esferas alejadas
Se tienen un sistema de dos esferas conductoras (“1” y “2”) muy alejadas entre sí, de radios 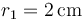 , y
, y 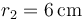 , respectivamente, que pueden unirse por un hilo conductor de 100 Ω. No hay más cargas ni conductores en el sistema. Inicialmente la esfera 1 almacena una carga de 20 nC y la esfera 2 una carga de 40 nC.
, respectivamente, que pueden unirse por un hilo conductor de 100 Ω. No hay más cargas ni conductores en el sistema. Inicialmente la esfera 1 almacena una carga de 20 nC y la esfera 2 una carga de 40 nC.
10.1 Pregunta 1
Una vez que se conectan por el hilo…
- A no fluye corriente alguna por el hilo.
- B no hay información suficiente para saber hacia dónde va la corriente.
- C fluye una intensidad de corriente que va de la esfera 1 a la 2.
- D fluye una intensidad de corriente que va de la esfera 2 a la 1.
10.1.1 Solución
La respuesta correcta es la C.
La corriente eléctrica fluye de mayor a menor potencial. Por tanto, se trata de hallar el potencial al que se encuentra cada esfera y ver cuál es mayor.
Al estar las dos esferas alejadas, podemos considerar que cada una no influye en la otra. En ese caso, el potencial al que se encuentra cada una es el mismo que para una esfera aislada:
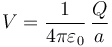
Para la primera esfera
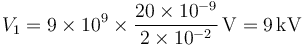
y para la segunda
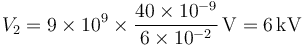
Vemos que, aunque tiene menos carga, el potencial de la primera esfera es más alto (por ser mucho más pequeña), por tanto, la corriente fluye de la esfera 1 a la 2, hasta que se igualen los potenciales.
10.2 Pregunta 2
Entre el estado inicial y el estado de equilibrio final, ¿cuánta energía se ha disipado en el hilo conductor?
- A 7.5 μJ
- B 210 μJ
- C 15 μJ
- D 202.5 μJ
10.2.1 Solución
La respuesta correcta es la A.
La energía total disipada en la resistencia es igual a la diferencia entre la que había almacenada al principio y la que queda almacenada al final.
La energía inicial almacenada en el sistema es
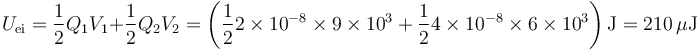
Para hallar la energia final necesitamos saber cómo quedan distribuidas las cargas y potenciales en ese estado.
Tenemos que la carga total se conserva en todo instante, por lo que
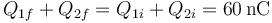
El estado de equilibrio se alcanza cuando se igualan los potenciales, lo que implica que
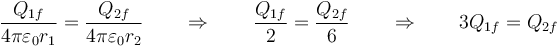
Ya tenemos un sistema de dos ecuaciones con dos incógnitas, con solución

y el potencial final de ambas esferas es
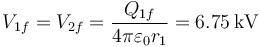
Por tanto, la energía almacenada en el estado final es
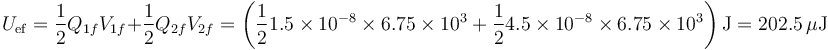
Por tanto, la energía disipada en la resistencia es
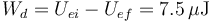
Nótese que el valor de la resistencia del cable es irrelevante.
De hecho, estas dos preguntas podrían haberse resuelto con los conocimientos del tema de electrostática en el vacío (salvo en el concepto de energía disipada en una resistencia).
11 Circuito con condensador y resistencias
Dado el circuito de la figura,
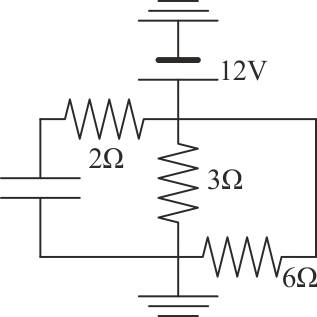
11.1 Pregunta 1
¿cuánto vale la corriente eléctrica que sale del generador?
- A 12 A
- B 4 A
- C 6 A
- D 1.09 A
11.1.1 Solución
La respuesta correcta es la C.
11.2 Pregunta 2
¿Cuánto vale la diferencia de potencial entre las placas del condensador?
- A 0 V
- B 12 V
- C 4 V
- D No hay información suficiente para determinarla.
11.2.1 Solución
La respuesta correcta es la B.
12 Dos hilos en paralelo
Un cable por el que circula una cierta corriente I0 se separa en dos hilos en paralelo del mismo material y la misma longitud, siendo el “1” de 3 mm de diámetro y el “2” de 1 mm de diámetro. ¿Cómo se reparte la corriente entre los dos hilos?
- A El 1 el 90% y el 2 el 10%.
- B El 1 el 25% y el 2 el 75%.
- C El 1 el 75% y el 2 el 25%.
- D El 1 el 50% y el 2 el 50%
12.1 Solución
La respuesta correcta es la A.





