Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del movimiento rectilíneo (GIE)

De Laplace

Revisión a fecha de 09:16 8 oct 2012; Antonio (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Aproximación numérica de la velocidad y la aceleración

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
x (m) 0.00 -0.04 -0.06 -0.06 -0.04 0.00 0.06 0.14 0.24 0.36 0.50
  1. ¿En qué momento es máxima la velocidad? ¿En qué momento es nula? Calcule aproximadamente la velocidad en el intervalo entre t=0\,\mathrm{s} y t=1\,\mathrm{s}.
  2. Calcule aproximadamente la aceleración en el mismo intervalo.

2 Persecución policial

Las especificaciones del Seat Exeo establecen que va de 0 a 100 km/h en 9.2 s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegaría al otro lado?

Un Seat León amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Seat Exeo, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estába parado lo alcanza? ¿Qué velocidad tiene el coche patrulla cuando alcanza al infractor?

3 Ejemplo de movimiento rectilíneo no uniforme

Una partícula se mueve a lo largo de una recta de forma que su posición sigue la ley, en el SI

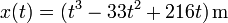
x(t) = (t^3-33t^2+216t)\,\mathrm{m}

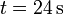entre t=0\,\mathrm{s} y t=24\,\mathrm{s}.

  1. Calcule la velocidad y la aceleración de este movimiento.
  2. ¿Cuál es la máxima distancia de la posición inicial a la que llega a encontrarse la partícula? ¿Cuánto vale el desplazamiento neto a lo largo del intervalo? ¿Y la distancia total recorrida?
  3. ¿Cuánto valen la máxima y la mínima rapidez de este movimiento?

4 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

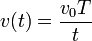
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre t = T y t = 3T?

5 Ejemplos de velocidad en función de la posición

1) La velocidad de una partícula sigue la ley

v = \sqrt{Ax}

siendo x la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2) Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

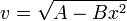
v = \sqrt{A- B x^2}

con A y B constantes positivas.

  1. ¿En que se medirá B en el SI?
  2. ¿Cómo depende de la posición la aceleración de la partícula?

6 Aceleración en un tramo rectilíneo

La longitud de la recta principal del circuito de Monza mide 1.3 km. Un Ferrari entra en la recta a 260 km/h y acelera durante 0.8 km hasta alcanzar 340 km/h. Mantiene esta velocidad hasta estar a 150 m de la primera chicane, a partir de ahí frena y llega la chicane a 80 km/h. Un Red Bull entra en la misma recta a 280 km/h, acelera hasta 320 km/h durante 0.5 km y frena al llegar a 120 m de la chicane, en la que entra a 90 km/h.

Suponiendo que las aceleraciones son constantes en cada uno de los tramos

  1. Determine las aceleraciones de los dos vehículos en cada uno de los tramos. Exprese los resultados como múltiplos de g.
  2. Calcule la velocidad media de cada uno. ¿Cuál tarda menos en recorrer la recta?
  3. Represente las gráficas de velocidad frente a la posición y frente al tiempo.

7 Ejemplo de integración numérica

Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica

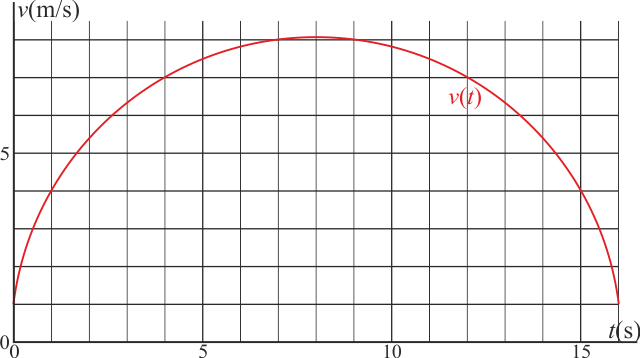
Archivo:velocidad-circulo.png

La partícula parte de s = 0.

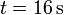  1. Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en t=16\,\mathrm{s}.
  2. Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es
v = \sqrt{1+16t-t^2}
¿Cuál es el error relativo cometido en el apartado anterior?

8 Calculo gráfico de velocidad media

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

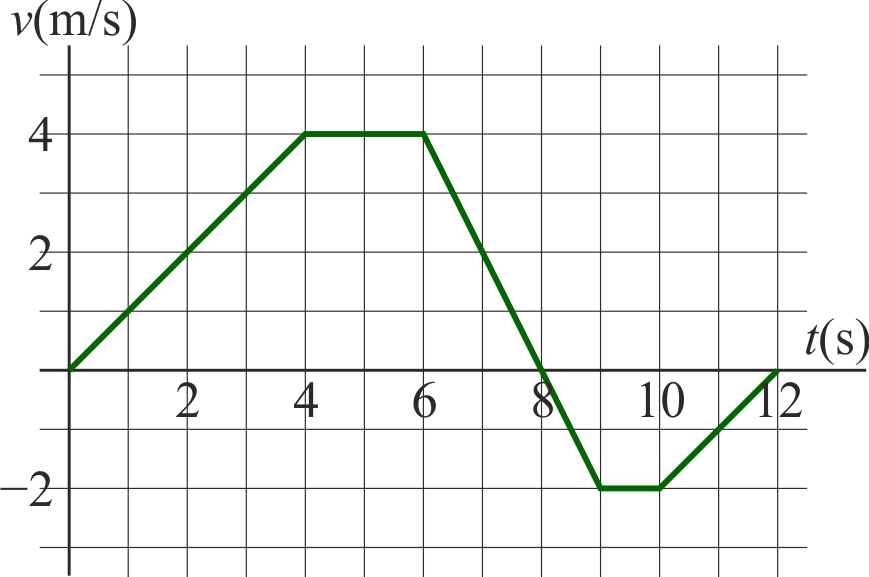
Archivo:velocidad-quebrada.png
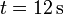  1. ¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?
  2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

9 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

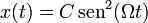
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

10 Movimiento con aceleración tangencial constante

Una partícula se mueve a lo largo de una circunferencia de radio R en el plano OXY con centro el origen, de forma que su aceleración tangencial es constante. ¿Cómo varía con el tiempo la aceleración normal de este movimiento?

11 Cálculo de aceleración en una curva

Un coche entra en una curva de 90° y 100 m de radio a 80 km/h. Disminuye su rapidez uniformemente hasta salir de la curva a 50 km/h.

  1. Determine su rapidez cuando ha recorrido 1/3 de la curva, la mitad y 2/3 de ella.
  2. Halle su aceleración tangencial y su aceleración normal en los mismos puntos.
  3. Exprese el vector aceleración en estos puntos en los ejes indicados en la figura
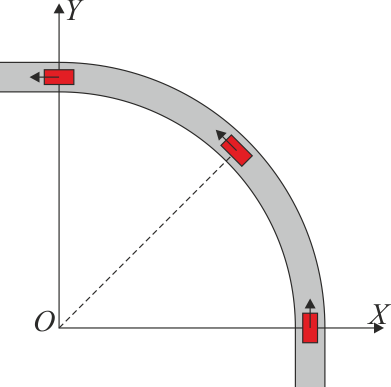
Archivo:aceleracion-coche-curva.png

12 Cálculos a partir de magnitudes cinemáticas instantáneas

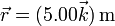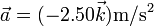En un instante dado, una partícula ocupa la posición \vec{r}=(5.00\vec{k})\,\mathrm{m}, tiene una velocidad \vec{v}=(4.00\vec{\jmath}+3.00\vec{k})\mathrm{m}/\mathrm{s} y una aceleración \vec{a}=(-2.50\vec{k})\mathrm{m}/\mathrm{s}^2.

  1. ¿Cuánto valen en dicho instante su aceleración tangencial y su aceleración normal, medidas en m/s²?
  2. ¿Cuánto vale el radio de curvatura en dicho instante?
  3. ¿Cuál es su posición en m y su velocidad en m/s un tiempo 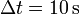\Delta t = 10\,\mathrm{s} más tarde?

13 Anilla ensartada en dos varillas

Una pequeña anilla P se encuentra ensartada en la intersección de dos barras giratorias. Los extremos fijos de las barras distan una cantidad L y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:

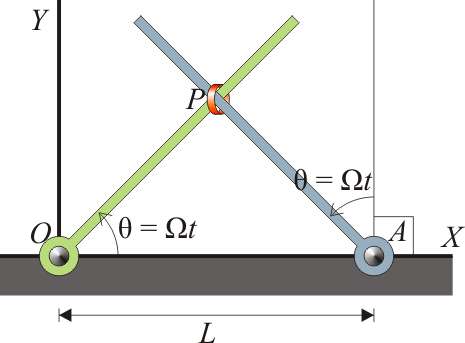
Archivo:anilla-dos-varillas.png
  1. ¿Cuáles son las ecuaciones horarias de P?
  2. ¿Qué clase de trayectoria describe?
  3. ¿Qué tipo de movimiento realiza?

14 Movimiento en un tiro parabólico

Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

\vec{a}(t)=-g\vec{k}

una posición inicial nula (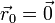\vec{r}_0=\vec{0}) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.

  1. Determine el vector de posición, la velocidad y la aceleración en cada instante.
  2. Halle el punto donde la partícula impacta con el suelo. ¿Cuál es el alcance máximo para una rapidez inicial dada?
  3. Calcule la celeridad y el vector tangente en el instante inicial y en el instante en que se encuentra a mayor altura.
  4. Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los dos instantes anteriores.
  5. Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
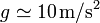  6. Suponga que se quiere alcanzar un blanco situado a 60 m con un mortero que comunica una rapidez inicial de 25 m/s. ¿Con qué ángulo debe dispararse si en medio se encuentra un eucalipto de 15 m de altura? (supóngase g\simeq 10\,\mathrm{m}/\mathrm{s}^2)

15 Caída de un proyectil lanzado horizontalmente

Una partícula se lanza horizontalmente con una rapidez de 8.0 m/s desde una torre de 20.0 m de altura, estando sometida exclusivamente a la aceleración de la gravedad.

  1. ¿Cuánto tarda aproximadamente en impactar con el suelo y a qué distancia de la torre lo hace?
  2. ¿Con qué rapidez impacta con el suelo?

16 Estudio de un movimiento tridimensional

Una partícula se mueve según las ecuaciones horarias

\vec{r}(t)=A\cos^2(\omega t)\vec{\imath}+2A\,\mathrm{sen}^2(\omega t)\vec{\jmath}+2A\cos^2(\omega t)\vec{k}
  1. ¿Qué trayectoria sigue la partícula?
  2. Determine la ley horaria s(t). Suponga que s(0) = 0.
  3. ¿Qué tipo de movimiento describe la partícula?

17 Evolvente de una circunferencia

La evolvente de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio A que se va desenrollando a ritmo constante, de forma que el punto C donde el hilo deja de hacer contacto con el carrete forma un ángulo θ = ωt con el eje OX. Una partícula material se encuentra en el punto P situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.

  1. Determine el vector de posición de la partícula.
  2. Calcule la velocidad y la aceleración de la partícula.
  3. Determine la distancia recorrida por la partícula como función del tiempo, s = s(t).
  4. Halle los vectores tangente y normal a la trayectoria.
  5. Halle el radio de curvatura y el centro de curvatura.

18 Ejemplo de movimiento expresado en polares

Una partícula describe una curva cuya ecuación en coordenadas polares es

\rho = A\cos(\Omega t)\qquad\qquad \varphi = \Omega t
  1. Calcule la velocidad y la aceleración en cada instante.
  2. Halle las componentes intrínsecas de la aceleración para todo t.
  3. Calcule el radio y el centro de curvatura en todo momento.
  4. ¿De qué tipo de movimiento se trata?

19 Caso de movimiento circular

Una partícula describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple

\omega = k\varphi\,

con k una constante y \varphi el ángulo que el vector de posición instantánea forma con el eje OX.

  1. Determine la aceleración angular de la partícula como función del ángulo \varphi.
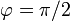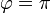  2. Halle las componentes intrínsecas de la aceleración lineal en \varphi = \pi/2 y \varphi = \pi.
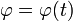  3. Determine la ley horaria \varphi = \varphi(t).

20 Movimiento oscilatorio circular

Una partícula se mueve sobre la circunferencia, expresada en polares y en el SI, 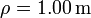\rho = 1.00\,\mathrm{m}, siguiendo la ley horaria

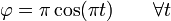
\varphi = \pi \cos(\pi t)\qquad \forall t

con \varphi el ángulo que el vector de posición forma con el eje OX positivo.

  1. Determine la aceleración angular en t = (1 / 3)s
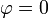
  2. Halle la velocidad lineal cuando pasa por \varphi=0
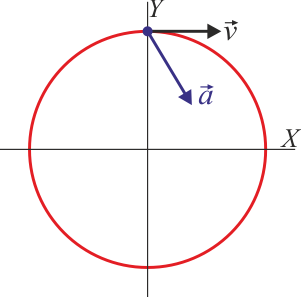
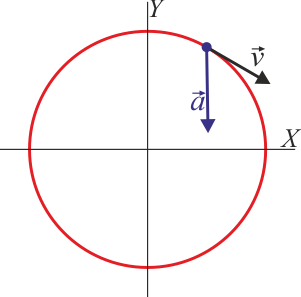
  3. Indique cuál de las siguientes cuatro figuras corresponde a la velocidad y la aceleración en t = (1 / 3)s
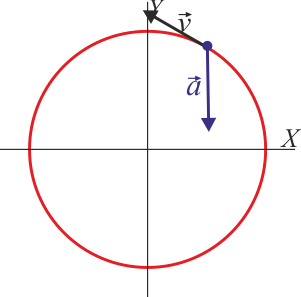
Archivo:va-circular-oscilatorio-01.png Archivo:va-circular-oscilatorio-02.png
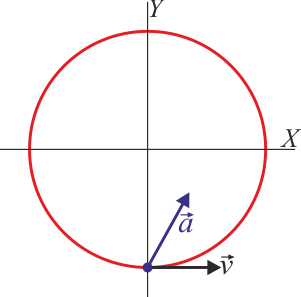
Archivo:va-circular-oscilatorio-03.png Archivo:va-circular-oscilatorio-04.png

21 Ejemplo de movimiento helicoidal

El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como

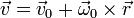
\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}

siendo

\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}_0=\omega_0 \vec{k}

dos vectores constantes. Si la posición inicial es 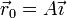\vec{r}_0=A\vec{\imath}

  1. Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas.
  2. Determine las ecuaciones horarias ρ = ρ(t), 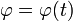\varphi=\varphi(t) y z = z(t). ¿Cuánto vale el paso de rosca de la hélice, esto es, lo que sube en el tiempo que da una vuelta alrededor del eje?
  3. Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento.
  4. Determine el radio de curvatura de la trayectoria en cualquier instante.

22 Espiral logarítmica

Una partícula describe una espiral logarítmica a partir de t = 0 de manera que, en el SI y empleando coordenadas polares,

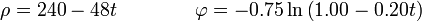
\rho = 240-48t\qquad\qquad \varphi = -0.75\ln\left(1.00-0.20t\right)
  1. Halle la velocidad en cada instante.
  2. Calcule la rapidez del movimiento como función del tiempo.
  3. ¿Cuánto tiempo tarda la partícula en llegar al origen de coordenadas? ¿Cuántas vueltas alrededor del origen da en ese tiempo?
  4. Halle la aceleración para cada instante, así como sus componentes intrínsecas
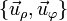
  5. Calcule los vectores tangente y normal a la trayectoria en cada punto de ésta, en función de la base \{\vec{u}_\rho,\vec{u}_\varphi\}
  6. Calcule el radio de curvatura como función del tiempo.
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_movimiento_rectil%C3%ADneo_(GIE)"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace