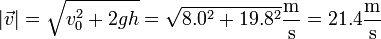Caída de un proyectil lanzado horizontalmente

De Laplace

1 Enunciado

Una partícula se lanza horizontalmente con una rapidez de 8.0 m/s desde una torre de 20.0 m de altura, estando sometida exclusivamente a la aceleración de la gravedad.

¿Cuánto tarda aproximadamente en impactar con el suelo y a qué distancia de la torre lo hace?
¿Con qué rapidez impacta con el suelo?

2 Tiempo y distancia de impacto

El movimiento de una partícula sometida exclusivamente a la acción de la gravedad es un movimiento parabólico, cuya ecuación horaria es

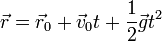
$\vec{r}=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{g}t^2$

donde

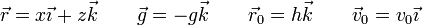
$\vec{r}=x\vec{\imath}+z\vec{k}\qquad \vec{g}=-g\vec{k}\qquad\vec{r}_0 = h\vec{k}\qquad\vec{v}_0 = v_0\vec{\imath}$

lo que nos da

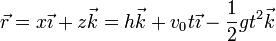
$\vec{r}=x\vec{\imath}+z\vec{k} = h\vec{k}+v_0t\vec{\imath}-\frac{1}{2}gt^2\vec{k}$

Separando por componentes

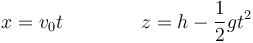
$x = v_0 t\qquad\qquad z = h -\frac{1}{2}gt^2$

El movimiento es una superposición de un movimiento uniforme en la dirección horizontal con uno uniformemente acelerado en la vertical.

El impacto se produce cuando la altura se hace igual a 0.

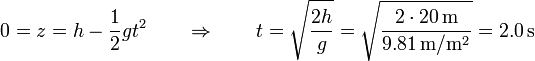
$0 = z = h - \frac{1}{2}gt^2\qquad\Rightarrow\qquad t = \sqrt{\frac{2h}{g}}= \sqrt{\frac{2\cdot 20\,\mathrm{m}}{9.81\,\mathrm{m}/\mathrm{m}^2}} = 2.0\,\mathrm{s}$

La distancia de la torre a la cual impacta la da el desplazamiento horizontal en el mismo tiempo

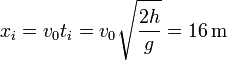
$x_i = v_0 t_i = v_0\sqrt{\frac{2h}{g}}=16\,\mathrm{m}$

3 Rapidez en el impacto

La velocidad con la que se mueve la partícula en cada instante es

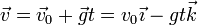
$\vec{v}=\vec{v}_0+\vec{g}t = v_0\vec{\imath}-gt\vec{k}$

En el momento del impacto esta velocidad vale

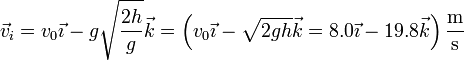
$\vec{v}_i = v_0\vec{\imath}-g\sqrt{\frac{2h}{g}}\vec{k}=\left(v_0\vec{\imath}-\sqrt{2gh}\vec{k}=8.0\vec{\imath}-19.8\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}$

La rapidez con la que impacta la masa es el módulo de esta velocidad

$|\vec{v}|=\sqrt{v_0^2+2gh}=\sqrt{8.0^2+19.8^2}\frac{\mathrm{m}}{\mathrm{s}} = 21.4\frac{\mathrm{m}}{\mathrm{s}}$

Caída de un proyectil lanzado horizontalmente

De Laplace

1 Enunciado

2 Tiempo y distancia de impacto

3 Rapidez en el impacto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES