Movimiento oscilatorio circular

De Laplace

Contenido

1 Enunciado
2 Aceleración angular
3 Velocidad lineal
4 Velocidad y aceleración

1 Enunciado

Una partícula se mueve sobre la circunferencia, expresada en polares y en el SI, 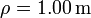$\rho = 1.00\,\mathrm{m}$ , siguiendo la ley horaria

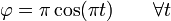
$\varphi = \pi \cos(\pi t)\qquad \forall t$

con $\varphi$ el ángulo que el vector de posición forma con el eje OX positivo.

Determine la aceleración angular en $t = (1 / 3)s$
Halle la velocidad lineal cuando pasa por $\varphi=0$
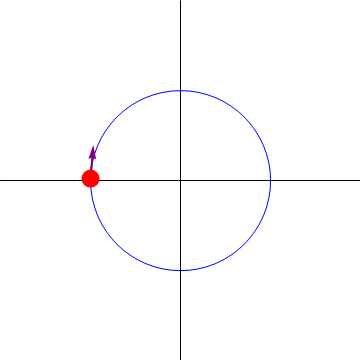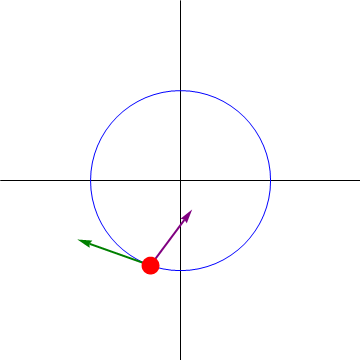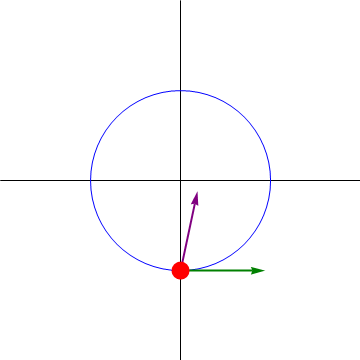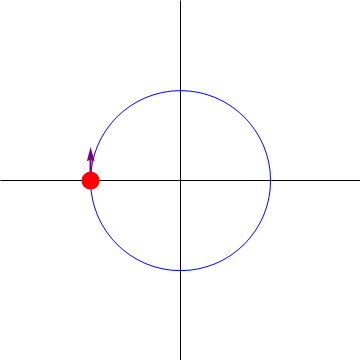
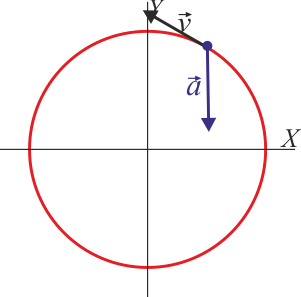
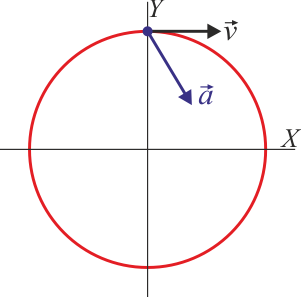
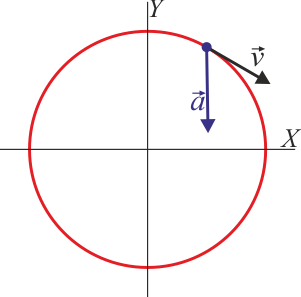
Indique cuál de las siguientes cuatro figuras corresponde a la velocidad y la aceleración en $t = (1 / 3)s$

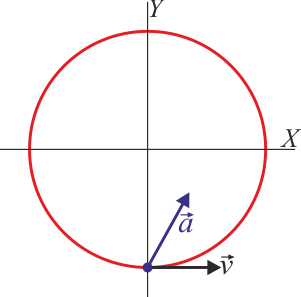
2 Aceleración angular

En el caso de un movimiento circular en el plano XY con centro el origen de coordenadas, la aceleración angular es un vector en la dirección del eje OZ y cuya componente vertical es igual a la segunda derivada del ángulo $\varphi$ respecto al tiempo

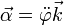
$\vec{\alpha}=\ddot{\varphi}\vec{k}$

En este caso

$\vec{\omega} = \dot{\varphi}\vec{k}=-\pi^2\mathrm{sen}(\pi t)\vec{k}\qquad\qquad \vec{\alpha} = -\pi^3\cos(\pi t)\vec{k}$

En $t = (1 / 3)s$ , su valor es

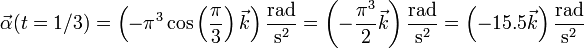
$\vec{\alpha}(t=1/3) = \left(-\pi^3\cos\left(\frac{\pi}{3}\right)\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}=\left(-\frac{\pi^3}{2}\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}=\left(-15.5\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}$

3 Velocidad lineal

La velocidad lineal en un movimiento circular la podemos calcular a partir de la velocidad angular y el vector de posición

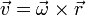
$\vec{v}=\vec{\omega}\times\vec{r}$

Cuando la partícula pasa por 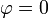$\varphi=0$ su posición es

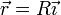
$\vec{r}=R\vec{\imath}$

por lo que

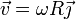
$\vec{v}=\omega R\vec{\jmath}$

La velocidad lineal, que es siempre tangente a la trayectoria, va en la dirección paralela al eje Y para este punto. No obstante, podría ser nula, por lo que debemos calcular el valor de la velocidad angular.

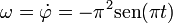
$\omega = \dot{\varphi}=-\pi^2\mathrm{sen}(\pi t)$

La partícula pasa por 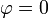$\varphi=0$ cuando

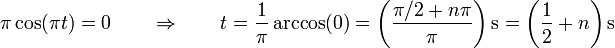
$\pi\cos(\pi t) = 0 \qquad\Rightarrow\qquad t = \frac{1}{\pi}\arccos(0) = \left(\frac{\pi/2+ n\pi}{\pi}\right)\mathrm{s}=\left(\frac{1}{2}+n\right)\mathrm{s}$

Para estos instantes

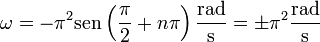
$\omega = -\pi^2\mathrm{sen}\left(\frac{\pi}{2}+n\pi\right)\frac{\mathrm{rad}}{\mathrm{s}}=\pm \pi^2\frac{\mathrm{rad}}{\mathrm{s}}$

El signo depende del valor de $n$ . Si n es par es negativo, y positivo si es impar. De aquí nos quedan los valores para la velocidad

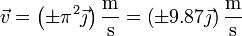
$\vec{v}=\left(\pm \pi^2\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}= \left(\pm 9.87\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}$

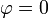Este resultado se puede visualizar observando que el movimiento que realiza la partícula es oscilatorio en la coordenada $\varphi$ , esto es, es análogo a un movimiento armónico simple, pero sobre una circunferencia en lugar de en línea recta. El punto $\varphi=0$ corresponde al punto central de la oscilación, en el que la velocidad es máxima, pudiendo ir en un sentido o en el opuesto.

4 Velocidad y aceleración

En principio las cuatro figuras corresponden a situaciones posibles del movimiento circular, por lo que sería necesario hallar cuánto vale la velocidad y la aceleración en el instante indicado para discernir entre las cuatro posibilidades.

Sin embargo, no es necesario. Nos basta con determinar la posición en el instante indicado. Cuando 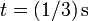$t = (1/3)\,\mathrm{s}$

$\varphi=\pi\cos\left(\frac{\pi}{3}\right)=\frac{\pi}{2}$

es decir, la partícula se encuentra en

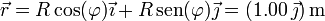
$\vec{r}=R\cos(\varphi)\vec{\imath}+R\,\mathrm{sen}(\varphi)\vec{\jmath}=(1.00\,\vec{\jmath})\,\mathrm{m}$

y hay una sola figura correspondiente a esta posición:

Podemos, no obstante, hallar la velocidad y la aceleración para este punto. Usando las expresiones en coordenadas polares se llega a que

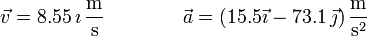
$\vec{v}=8.55\,\mathrm{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad \vec{a}=\left(15.5\vec{\imath}-73.1\,\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}^2}$

Este punto corresponde al primer cuarto de periodo. En él la rapidez está aumentando, y por tanto la aceleración tangencial es positiva. La aceleración normal es no nula y va hacia adentro de la circunferencia. Ello nos da el resultado de la figura.

Movimiento oscilatorio circular

De Laplace

Contenido

1 Enunciado

2 Aceleración angular

3 Velocidad lineal

4 Velocidad y aceleración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES