Inducción electromagnética
De Laplace
(→Aplicaciones de la ley de Faraday: generadores, motores y transformadores) |
(→Ley de inducción de Faraday) |
||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
==Ley de inducción de Faraday== | ==Ley de inducción de Faraday== | ||
| + | {{ac|Ley de Faraday}} | ||
| + | En situaciones de campos variables en el tiempo deja de cumplirse que el campo eléctrico sea irrotacional. | ||
| + | |||
| + | Cuando se tiene una espira $\Gamma$ que, en general, puede moverse o deformarse en el seno de un campo magnético variable en el tiempo, se | ||
| + | induce una fuerza electromotriz a lo largo de la espira que verifica la ''ley de Faraday'' en forma integral} | ||
| + | |||
| + | <center><math>\mathcal{E} = -\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | siendo <math>\Phi_m</math> el flujo magnético calculado sobre cualquier superficie apoyada en la curva <math>\Gamma</math> y orientada según la regla de la mano derecha respecto al sentido de recorrido de <math>\Gamma</math>. | ||
| + | |||
| + | Esta fuerza electromotriz contiene términos eléctricos y magnéticos, de acuerdo con la ley de fuerza de Lorentz | ||
| + | |||
| + | <center><math>\mathcal{E} = \oint_\Gamma (\mathbf{E}+\mathbf{v}\times\mathbf{B}){\cdot}\mathrm{d}\mathbf{r}</math>{{qquad}}{{qquad}}<math>\Phi_m = \int_S \mathbf{B}{\cdot}\mathrm{d}\mathbf{S} = \oint_\Gamma \mathbf{A}{\cdot}\mathrm{d}\mathbf{r}</math></center> | ||
| + | |||
| + | En principio, la ley de Faraday requiere una espira material en la cual las cargas experimenten la fuerza de Lorentz. Maxwell extendió este | ||
| + | resultado a una relación entre campos. Aplicando el teorema de Stokes a la versión integral se obtiene la forma diferencial de la ley de Faraday | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{E} = -\frac{\partial\mathbf{B}}{\partial t}</math></center> | ||
| + | |||
| + | que nos dice que el campo eléctrico posee fuentes vectoriales asociadas a la variación del campo magnético (ausentes, por tanto, en | ||
| + | electrostática). Esto implica que deja de existir el potencial eléctrico y el concepto de diferencia de potencial, siendo sustituido | ||
| + | por el de voltaje | ||
| + | |||
| + | <center><math>\Delta V = \int_{\!\!\!\!\!\!\!\!C\ A}^B \mathbf{E}{\cdot}\mathrm{d}\mathbf{r}</math></center> | ||
| + | |||
| + | donde es necesario indicar el camino $C$ a lo largo del cual se calcula la integral. | ||
| + | |||
| + | La condición de salto asociada a la ley de Faraday es la misma que en situaciones electrostáticas | ||
| + | |||
| + | <center><math>\mathbf{n}\times[\mathbf{E}] = \mathbf{0}</math></center> | ||
| + | |||
| + | aunque en esta forma sólo es aplicable a superficies inmóviles. | ||
| + | |||
| + | El signo negativo que precede a la derivada del flujo en la ley de Faraday implica la \emph{ley de Lenz}: el sentido de la corriente | ||
| + | inducida en la espira es tal que se opone a la variación del flujo magnético. | ||
| + | |||
==Coeficientes de inducción mutua y autoinducción== | ==Coeficientes de inducción mutua y autoinducción== | ||
Revisión de 11:20 7 abr 2009
Contenido |
1 Introducción
2 Ley de inducción de Faraday
En situaciones de campos variables en el tiempo deja de cumplirse que el campo eléctrico sea irrotacional.
Cuando se tiene una espira $\Gamma$ que, en general, puede moverse o deformarse en el seno de un campo magnético variable en el tiempo, se induce una fuerza electromotriz a lo largo de la espira que verifica la ley de Faraday en forma integral}
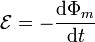
siendo Φm el flujo magnético calculado sobre cualquier superficie apoyada en la curva Γ y orientada según la regla de la mano derecha respecto al sentido de recorrido de Γ.
Esta fuerza electromotriz contiene términos eléctricos y magnéticos, de acuerdo con la ley de fuerza de Lorentz
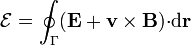
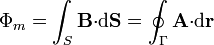
En principio, la ley de Faraday requiere una espira material en la cual las cargas experimenten la fuerza de Lorentz. Maxwell extendió este resultado a una relación entre campos. Aplicando el teorema de Stokes a la versión integral se obtiene la forma diferencial de la ley de Faraday
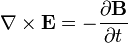
que nos dice que el campo eléctrico posee fuentes vectoriales asociadas a la variación del campo magnético (ausentes, por tanto, en electrostática). Esto implica que deja de existir el potencial eléctrico y el concepto de diferencia de potencial, siendo sustituido por el de voltaje
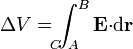
donde es necesario indicar el camino $C$ a lo largo del cual se calcula la integral.
La condición de salto asociada a la ley de Faraday es la misma que en situaciones electrostáticas
![\mathbf{n}\times[\mathbf{E}] = \mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
aunque en esta forma sólo es aplicable a superficies inmóviles.
El signo negativo que precede a la derivada del flujo en la ley de Faraday implica la \emph{ley de Lenz}: el sentido de la corriente inducida en la espira es tal que se opone a la variación del flujo magnético.





