Barra que cae en un campo magnético
De Laplace
Contenido |
1 Enunciado
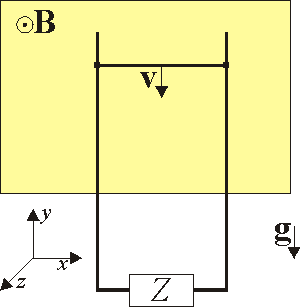
La figura representa un carril metálico superconductor por el cual puede deslizarse una varilla horizontal, también superconductora. Esta varilla está inmersa en un campo uniforme y cae por la acción de la gravedad
y cae por la acción de la gravedad
Inicialmente se encuentra en reposo y no circula intensidad por el circuito. En este momento se suelta. Determine la ecuación de movimiento y la posición de la varilla en función del tiempo si el circuito está cerrado por:
- Una resistencia

- Un condensador

- Una autoinducción
 .
.
Estudie en cada caso el balance energético del sistema.
2 Solución
2.1 Estudio general
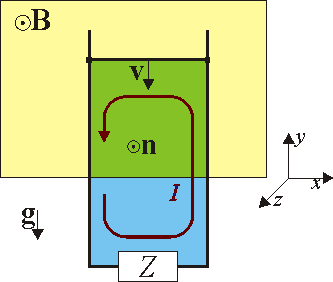
Al soltarse la barra, la gravedad hace que descienda aceleradamente. Sin embargo, al hacerlo, se modifica el área del circuito contenida en el campo magnético, dando lugar a una fuerza electromotriz, que generará una corriente. Esta corriente recorre todo el circuito, en particular la propia varilla, inmersa en el campo magnético. De acuerdo con la ley de Lorentz, aparecerá una fuerza sobre ésta, que será, simultáneamente, ortogonal a la corriente y al campo magnético, yendo por tanto en la dirección vertical y modificando el movimiento de la barra. También habrá fuerzas sobre el resto de los conductores, pero supondremos que éstos son rígidos y no se ven afectados por ella.
Consideraremos el origen de coordenadas justo en el borde inferior de la zona ocupada por el campo magnético, de forma que la altura a la que se encuentra la barra vendrá dada por el valor de y.
Según la segunda ley de Newton, la ecuación de movimiento para la barra es

donde directamente ya estamos suponiendo que todas las fuerzas son verticales.
Supongamos un sentido de recorrido del circuito, tal que la normal a él vaya en el mismo sentido que el campo magnético. En este caso, la corriente que atraviesa la barra irá en la dirección de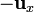 , con lo que la fuerza magnética será
, con lo que la fuerza magnética será

y la ecuación de movimiento
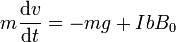
Para hallar una ecuación para la intensidad empleamos la ley de Faraday. En el circuito habrá una fuerza electromotriz debida al campo magnético que valdrá
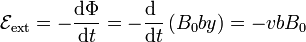
Esta fuerza electromotriz equivaldrá a la caída de tensión en el elemento de circuito exterior, esto es, será igual a
- En el caso de una resistencia:

- En el caso de un condensador:

- En el caso de un solenoide
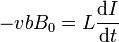
En cada caso resultará una ecuación de movimiento diferente
2.2 El caso de una resistencia
Para una resistencia se tiene el sistema
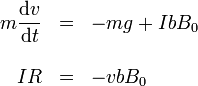
Reduciéndolo a una ecuación para la velocidad queda la ecuación diferencial
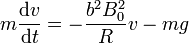
cuya solución para el caso de que la barra parta del reposo es

Vemos que la velocidad crece -con signo negativo-, pero no de forma uniforme, sino que tiende a un valor constante, para el cual se igualan la fuerza de la gravedad y la fuerza magnética.
La posición se obtiene integrando la ecuación anterior.
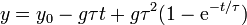
2.3 El caso de un condensador
Para el caso de un condensador tenemos el sistema
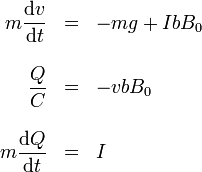
que, reducido a una sola ecuación es
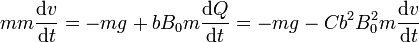
y de aquí

La solución de esta ecuación es
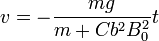
Vemos que la velocidad crece con el tiempo de forma uniforme, pero lo hace más lentamente que si no hubiera campo magnético.
La posición sigue la ecuación de un movimiento uniformemente acelerado
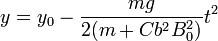
2.4 El caso de una autoinducción
Por último, para el caso de que haya una autoinducción presente tenemos que
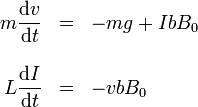
Reducimos este sistema derivando una vez
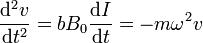
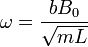
Esta es la ecuación de un oscilador armónico de frecuencia ω. La solución de esta ecuación, suponiendo que tanto la velocidad como la corriente inicial son nulas, es
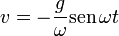
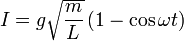
Según esto, tanto la velocidad como la intensidad de corriente oscilan armónicamente. La barra unas veces baja y otras sube. En cuanto a la posición, integrando una segunda vez
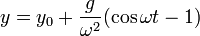
Esta es también una función oscilante. La barra baja hasta una altura mínima de valor
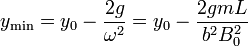
Si este valor no es negativo, lo que indicaría que la barra ha salido del campo magnético, la barra comienza a subir de nuevo hasta la posición inicial.
2.5 Balance energético
En cuanto a la energía, obtenemos su ecuación multiplicando la ecuación de movimiento por la velocidad

Reagrupando términos resulta
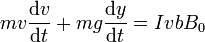
o, equivalentemente,
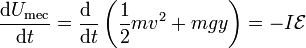
Esta ecuación expresa que la disminución de la energía mecánica, cinética más potencial, se debe al trabajo realizado sobre la corriente.
- Para el caso de una resistencia, esta ecuación se convierte en
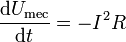
- Dado que el segundo miembro es siempre negativo, esta ecuación nos dice que la energía mecánica se esta perdiendo, en forma de calor, debido a la acción del campo magnético.
- Si se trata de un condensador tenemos
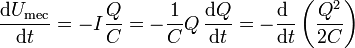
- o, equivalentemente,

- En este caso no hay pérdida de energía, sino que la energía potencial gravitatoria se transforma en parte en energía cinética y en parte en energía eléctrica almacenada en el condensador.
- Por último, para el caso de una autoinducción, se tiene que
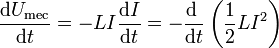
- o, lo que es lo mismo,
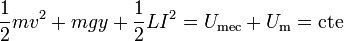
- Esta situación es similar a la del condensador, sólo que la energía mecánica se transforma en energía magnética. Esta energía es convertida en energía mecánica de nuevo, siguiendo un proceso oscilante.