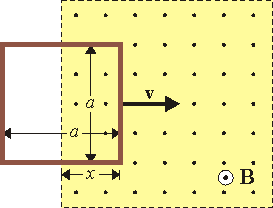
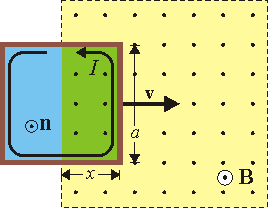
Frenado de espira cuadrada

De Laplace

Contenido

1 Enunciado
2 Cálculo de la corriente
3 Cálculo de la fuerza
4 Potencia disipada
5 Frenado magnético

1 Enunciado

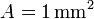Una espira cuadrada de lado $a=10\,\mathrm{cm}$ , hecha de un hilo de cobre de sección $A=1\,\mathrm{mm}^2$ penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo 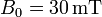$B_0=30\,\mathrm{mT}$ . La espira se mueve inicialmente con velocidad 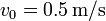$v_0=0.5\,\mathrm{m}/\mathrm{s}$ tangente a uno de sus lados y perpendicular al campo magnético. En

t = 0

la espira entra en el campo.

Calcule la corriente que se induce en la espira cuando la espira ha avanzado una distancia $x\,$ y se está moviendo con velocidad $v\,$ .
Halle la fuerza que el campo magnético ejerce con la espira.
Si la velocidad de la espira se mantiene constante, halle la potencia disipada en la espira por efecto Joule. ¿De dónde proviene la energía disipada?
Si se deja que la espira frene por acción del campo magnético, determine la evolución en el tiempo de la velocidad, así como la energía total disipada por efecto Joule.

2 Cálculo de la corriente

Como en otros problemas, obtenemos la corriente hallando la fuerza electromotriz por aplicación de la ley de Faraday y posteriormente calculamos la corriente aplicando la ley de ohm para un circuito.

Suponemos un sentido de recorrido tal que la normal a la superficie apoyada en la curva va en el mismo sentido que el campo magnético. En esta superficie el flujo magnético es igual a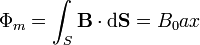 $\Phi_m = \int_S\mathbf{B}\cdot\mathrm{d}\mathbf{S} = B_0ax$

ya que aunque la espira es cuadrada, sólo el rectángulo de base $a$ y altura $x$ se encuentra dentro del campo magnético. La fuerza electromotriz en la espira es

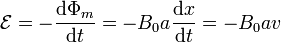
$\mathcal{E}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t} = -B_0a\frac{\mathrm{d}x}{\mathrm{d}t}=-B_0av$

y la corriente que circula por ella

$I=\frac{\mathcal{E}}{R}= -\frac{B_0av}{R}$

Vemos que, si la espira está entrando en el campo magnético, el sentido de la corriente es el contrario del que habíamos supuesto. Esto está de acuerdo con la ley de Lenz, pues la corriente inducida debe producir un flujo negativo para reducir el aumento del flujo magnético.

3 Cálculo de la fuerza

Al circular una corriente por la espira y encontrarse ésta en el seno de un campo magnético, aparece una fuerza sobre la espira, dada por la ley de Lorentz para una corriente

$\mathbf{F}=I\oint \mathrm{d}\mathbf{r}\times\mathbf{B}$

En este caso el campo magnético ejerce fuerza sobre tres de los lados, por estar el cuarto en el exterior. Asimismo, las fuerzas sobre los lados superior e inferior se cancelan, por ser iguales y opuestas. Queda la fuerza sobre la barra frontal, para la cual tenemos

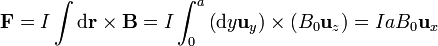
$\mathbf{F}=I\int \mathrm{d}\mathbf{r}\times\mathbf{B} = I\int_0^a \left(\mathrm{d}y\mathbf{u}_y\right)\times\left(B_0\mathbf{u}_z\right)= IaB_0\mathbf{u}_{x}$

Sustituyendo el valor de la corriente

$\mathbf{F}=-\frac{a^2B_0^2v}{R}\mathbf{u}_x=-\frac{a^2B_0^2}{R}\mathbf{v}$

Resulta una fuerza opuesta a la velocidad y proporcional a ella. Esta fuerza tiende a frenar la espira, funcionando como una fuerza de rozamiento viscoso.

4 Potencia disipada

Al circular una corriente por la espira y ser esta resistiva, se produce calor por efecto Joule, según la ley

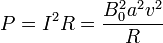
$P=I^2R=\frac{B_0^2a^2v^2}{R}$

De acuerdo con la ley de conservación de la energía, esta potencia disipada debe provenir de algún sitio, sea de la energía almacenada en el sistema, sea de algún aporte externo de energía.

El origen mecánico de esta energía está en la fuerza de frenado ejercida por el campo magnético, la cual desarrolla una potencia

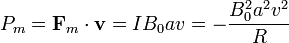
$P_m = \mathbf{F}_m\cdot\mathbf{v}= IB_0av =-\frac{B_0^2a^2v^2}{R}$

Por tanto, el campo magnético extrae del sistema exactamente la misma energía por unidad de tiempo que se está disipando. Funciona así como intermediario, convirtiendo energía mecánica en calor (esto es, frenando el sistema).

Si la velocidad de la espira permanece constante, es porque existe un agente externo que empuja la espira, venciendo la fuerza magnética.

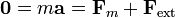
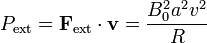
$\mathbf{0}=m\mathbf{a}=\mathbf{F}_m+\mathbf{F}_\mathrm{ext}$ $P_\mathrm{ext}=\mathbf{F}_\mathrm{ext}\cdot\mathbf{v}=\frac{B_0^2a^2v^2}{R}$

Vemos entonces que si hay un agente empujando la espira, dicho agente realiza un trabajo por unidad de tiempo igual a la potencia disipada en forma de calor.

5 Frenado magnético

Si no hay ningún agente externo empujando la espira, ésta se ve frenada por el campo magnético. Aplicando la segunda ley de Newton

$m\mathbf{a}=m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=-\frac{B_0^2a^2}{R}\mathbf{v}$

La solución de esta ecuación diferencial es una exponencial decreciente

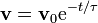
$\mathbf{v}=\mathbf{v}_0\mathrm{e}^{-t/\tau}\,$

con un tiempo típico de frenado

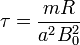
$\tau=\frac{mR}{a^2B_0^2}\,$

La posición de la espira la obtenemos integrando una vez más

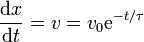
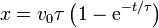
$\frac{\mathrm{d}x}{\mathrm{d}t} = v = v_0\mathrm{e}^{-t/\tau}$ $x = v_0\tau\left(1-\mathrm{e}^{-t/\tau}\right)$

Este resultado implica que aunque la espira nunca llega a detenerse del todo, la profundidad de penetración si alcanza un límite igual a $v 0 τ$ .

Si calculamos la energía total disipada durante el proceso de frenado,

$W_d = \int_0^\infty P_d\,\mathrm{d}t = \int_0^\infty \frac{B_0^2a^2v_0^2}{R}\mathrm{e}^{-2t/\tau}\mathrm{d}t=\frac{B_0^2a^2v_0^2}{R}\frac{\tau}{2}$

y, sustituyendo el valor del tiempo característico de frenado

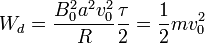
$W_d = \frac{B_0^2a^2v_0^2}{R}\frac{\tau}{2} = \frac{1}{2}mv_0^2$

que no es otra cantidad que la energía cinética inicial. El campo magnético frena la espira y, a falta de un agente externo, la energía disipada procede de la energía mecánica inicial, que en este caso era toda cinética.

El tiempo característico de frenado es, para una espira cuadrada de un material de densidad de masa $ρ m$

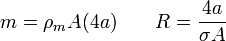
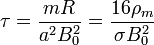
$m = \rho_m A(4a)\qquad R = \frac{4a}{\sigma A}$ $\tau=\frac{mR}{a^2B_0^2}= \frac{16\rho_m}{\sigma B_0^2}$

esto es, siempre que se trate de un conductor filiforme, es independiente de las dimensiones de la espira (y, por supuesto, de su velocidad inicial). Para el caso de un hilo de cobre en un campo de 30 mT

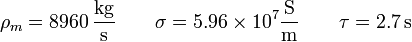
$\rho_m = 8960\,\frac{\mathrm{kg}}{\mathrm{s}}\qquad \sigma = 5.96\times 10^7 \frac{\mathrm{S}}{\mathrm{m}}\qquad \tau = 2.7\,\mathrm{s}$

Donde sí intervienen las dimensiones de la espira es en averiguar si la espira llega a detenerse. Para los datos del problema, la profundidad de penetración es

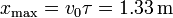
$x_\mathrm{max}=v_0\mathrm{\tau}= 1.33\,\mathrm{m}$

que es mucho mayor que las dimensiones de la espira. Esto quiere decir que lo que ocurre realmente es que la espira se va frenando hasta el momento en que penetra del todo. En ese momento se detiene la fuerza electromotriz y el efecto de frenado, por lo que la espira continua moviéndose con velocidad constante (hasta que salga por el otro lado del campo, momento en que vuelve a frenarse).

Frenado de espira cuadrada

De Laplace

Contenido

1 Enunciado

2 Cálculo de la corriente

3 Cálculo de la fuerza

4 Potencia disipada

5 Frenado magnético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES