Inducción mutua de dos anillos

De Laplace

1 Enunciado

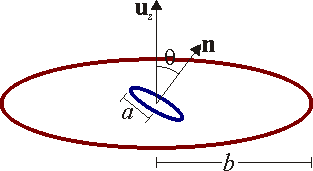
Se tienen dos anillos metálicos. Ambos anillos están centrados en el origen de coordenadas. Uno de ellos posee radio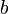 $b\,$ y está situado en el plano

X Y

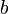. El otro, de radio $a\,$ , está inclinado, de forma que su normal forma un ángulo $\theta\,$ con el eje $z\,$ . El radio $b\,$ es mucho mayor que $a\,$ .

Determine el coeficiente de inducción mutua entre los dos anillos a partir del flujo del campo del anillo exterior a través del anillo interior (tenga en cuenta que éste es muy pequeño) cuando por el anillo exterior circula una corriente $I 1$ .
Halle el coeficiente de inducción mutua a partir del flujo del campo del anillo interior (que es prácticamente un dipolo) a través del anillo exterior cuando por el anillo interior circula una corriente $I 2$ . ¿Son iguales los dos coeficientes?

2 Inducción del anillo exterior en el interior

La expresión analítica del campo magnético creado por una espira es extremadamente compleja, requiriendo el uso de integrales elípticas. Sólo en los puntos de su eje posee expresión sencilla. Sin embargo, esto es todo lo que necesitamos, pues, si el anillo interior es muy pequeño, podemos suponer que el campo magnético debido al anillo exterior es uniforme y, de hecho, tiene el mismo valor que justo en el centro de la espira, donde vale

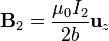
$\mathbf{B}_2=\frac{\mu_0 I_2}{2 b}\mathbf{u}_{z}$

siendo $I 2$ la corriente que circula por el anillo 2 y $b$ su radio.

Si suponemos que el campo es prácticamente uniforme, el flujo del mismo a través del anillo interior es inmediato

$\Phi_{12}=\int_{S_1}\mathbf{B}_2{\cdot}\mathrm{d}\mathbf{S}_1=\mathbf{B}_2{\cdot}\mathbf{S}_1$

y el vector superficie correspondiente al anillo interior tiene por módulo el área y por dirección la de la normal a la espira

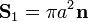
$\mathbf{S}_1=\pi a^2\mathbf{n}$

por lo que el flujo será

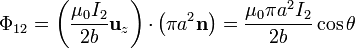
$\Phi_{12}=\left(\frac{\mu_0I_2}{2b}\mathbf{u}_{z}\right){\cdot}\left(\pi a^2\mathbf{n}\right)=\frac{\mu_0\pi a^2 I_2}{2b}\cos\theta$

y de aquí resulta el coeficiente de inducción mutua

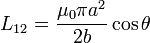
$L_{12}=\frac{\mu_0 \pi a^2}{2b}\cos\theta$

3 Inducción del anillo interior en el exterior

Si partimos del campo creado por la espira interior, la aproximación anterior deja de ser válida. Obviamente, el campo creado por la espira pequeña no es el mismo en todos los puntos de una superficie apoyada en la espira grande.

Lo que si podemos hacer es suponer que el anillo interior es tan pequeño, que puede ser aproximado por un dipolo magnético puntual, con momento magnético

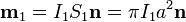
$\mathbf{m}_1=I_1S_1\mathbf{n}=\pi I_1 a^2\mathbf{n}$

A este dipolo le corresponde un potencial vector

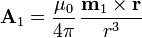
$\mathbf{A}_1=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}_1\times\mathbf{r}}{r^3}$

y un campo magnético

$\mathbf{B}_1=\frac{\mu_0}{4\pi}\,\frac{3(\mathbf{m}_1{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m}_1}{r^5}$

El flujo de este campo lo calculamos sobre una superficie apoyada en la circunferencia de radio $b$ . La superficie más simple no es el círculo, ya que este atraviesa la espira pequeña, lo que implica la aparición de una singularidad y el tener que tratar con campos infinitos. En su lugar, la superficie más adecuada es una semiesfera apoyada en la misma circunferencia. Sobre esta superficie todos los puntos se encuentran a la misma distancia, $b$ , del dipolo. El flujo es

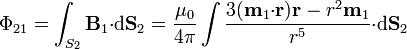
$\Phi_{21}=\int_{S_2}\mathbf{B}_1{\cdot}\mathrm{d}\mathbf{S}_2=\frac{\mu_0}{4\pi} \int\frac{3(\mathbf{m}_1{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m}_1}{r^5}{\cdot}\mathrm{d}\mathbf{S}_2$

En esta superficie

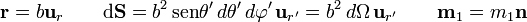
$\mathbf{r}=b\mathbf{u}_{r}\qquad \mathrm{d}\mathbf{S}=b^2\,\mathrm{sen}\theta'\,d\theta'\,d\varphi'\,\mathbf{u}_{r'}=b^2\,d\Omega\,\mathbf{u}_{r'}\qquad\mathbf{m}_1=m_1\mathbf{n}$

y la integral se reduce a

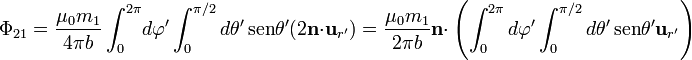
$\Phi_{21}=\frac{\mu_0 m_1}{4\pi b}\int_0^{2\pi}\!d\varphi'\int_0^{\pi/2}d\theta'\,\mathrm{sen}\theta' (2\mathbf{n}{\cdot}\mathbf{u}_{r'})= \frac{\mu_0m_1}{2\pi b}\mathbf{n}{\cdot}\left(\int_0^{2\pi}d\varphi'\int_0^{\pi/2} d\theta'\,\mathrm{sen}\theta'\mathbf{u}_{r'}\right)$

Sustituyendo

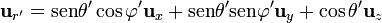
$\mathbf{u}_{r'}=\mathrm{sen}\theta'\cos\varphi'\mathbf{u}_{x}+\mathrm{sen}\theta'\mathrm{sen}\varphi'\mathbf{u}_{y}+\cos\theta'\mathbf{u}_{z}$

la integral de las componentes $x$ e $y$ se anulan, mientras que la $z$ da

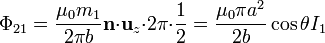
$\Phi_{21}=\frac{\mu_0m_1}{2\pi b}\mathbf{n}{\cdot}\mathbf{u}_{z}{\cdot}2\pi{\cdot}\frac{1}{2}=\frac{\mu_0\pi a^2}{2b}\cos\theta I_1$

de donde resulta un coeficiente de inducción mutua

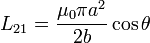
$L_{21}=\frac{\mu_0\pi a^2}{2b}\cos\theta$

que es igual al obtenido anteriormente.

A la hora de calcular el flujo magnético podemos hacer uso de la identidad (consecuencia del teorema de Stokes)

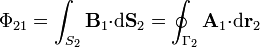
$\Phi_{21}=\int_{S_2}\mathbf{B}_1{\cdot}\mathrm{d}\mathbf{S}_2=\oint_{\Gamma_2}\mathbf{A}_1{\cdot}\mathrm{d}\mathbf{r}_2$

con lo que el flujo vale

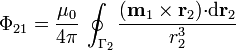
$\Phi_{21}=\frac{\mu_0}{4\pi}\,\oint_{\Gamma_2}\frac{(\mathbf{m}_1\times\mathbf{r}_2){\cdot}\mathrm{d}\mathbf{r}_2}{r_2^3}$

Ahora bien, por las propiedades del producto mixto

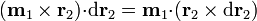
$(\mathbf{m}_1\times\mathbf{r}_2){\cdot}\mathrm{d}\mathbf{r}_2=\mathbf{m}_1{\cdot}(\mathbf{r}_2\times \mathrm{d}\mathbf{r}_2)$

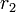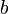y el módulo $r_2\,$ vale $b\,$ para todos los puntos de la espira de fuera. Por tanto

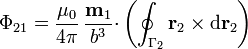
$\Phi_{21}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}_1}{b^3}{\cdot}\left(\oint_{\Gamma_2}\mathbf{r}_2\times \mathrm{d}\mathbf{r}_2\right)$

La integral resultante aparece en la teoría del desarrollo multipolar magnético, y equivale a

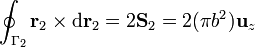
$\oint_{\Gamma_2}\mathbf{r}_2\times \mathrm{d}\mathbf{r}_2=2\mathbf{S}_2=2(\pi b^2)\mathbf{u}_{z}$

El flujo será entonces

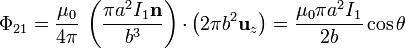
$\Phi_{21}=\frac{\mu_0}{4\pi}\,\left(\frac{\pi a^2I_1\mathbf{n}}{b^3}\right){\cdot}\left(2\pi b^2\mathbf{u}_{z}\right)=\frac{\mu_0\pi a^2I_1}{2b}\cos\theta$ como ya obtuvimos antes.

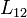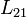Aunque cabía esperar la igualdad entre $L_{12}\,$ y $L_{21}\,$ , hay que ser precavido con el hecho de que estamos trabajando con una aproximación al verdadero coeficiente, y por tanto, pudiera ser que el grado de aproximación fuera diferente en cada caso. No es así.

En cuanto al error cometido, si se estima el orden de magnitud de los términos despreciados, se ve que estos son de orden 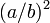$(a/b)^2\,$ , esto es, que si la espira de fuera es diez veces mayor que la de dentro, el error es en torno al 1%.

Inducción mutua de dos anillos

De Laplace

1 Enunciado

2 Inducción del anillo exterior en el interior

3 Inducción del anillo interior en el exterior

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES