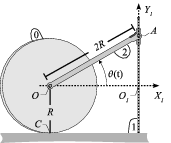Problemas de Movimiento plano (G.I.A.)

De Laplace

Revisión de 23:44 7 ene 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Disco que arrastra una varilla) ← Edición más antigua		Revisión de 00:00 8 ene 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Disco que arrastra una varilla) Edición más nueva →
Línea 93:		Línea 93:
	# Exprese el vector de posición del punto <math>A</math> en el sistema &ldquo;1&rdquo;, <math>\mathbf{r}_{21}^A</math>, en función de un ángulo <math>\beta</math> arbitrario.		# Exprese el vector de posición del punto <math>A</math> en el sistema &ldquo;1&rdquo;, <math>\mathbf{r}_{21}^A</math>, en función de un ángulo <math>\beta</math> arbitrario.
	# Si <math>\dot{\beta}=-\Omega</math>, con <math>\Omega</math> constante y positiva, calcule <math>\mathbf{v}_{21}^A(t)</math> y <math>\mathbf{a}_{21}^A(t)</math> para todo instante de tiempo, en función de <math>\beta</math>, <math>\Omega</math> y <math>R</math>.		# Si <math>\dot{\beta}=-\Omega</math>, con <math>\Omega</math> constante y positiva, calcule <math>\mathbf{v}_{21}^A(t)</math> y <math>\mathbf{a}_{21}^A(t)</math> para todo instante de tiempo, en función de <math>\beta</math>, <math>\Omega</math> y <math>R</math>.
		+
		+	==[[ Aplicación:Disco_empujando_una_varilla_articulada_en_él | Disco con varilla articulada]]==
		+	Un disco de radio <math>R</math> (sólido "0"), se mueve contenido siempre en el mismo plano vertical <math>OXY</math>.
		+	El centro <math>C</math> del disco realiza un movimiento rectilíneo uniforme con velocidad <math>v_0</math> respecto del plano horizontal fijo (sólido "1"),
		+	sobre el que rueda sin deslizar. Un barra rígida de longitud <math>4R</math> (sólido "2"), contenida también en <math>OXYZ</math>, tiene su extremo <math>A</math>
		+	articulado en un punto del perímetro del disco, mientras que su extremo <math>B</math> se desliza sobre el plano horizontal.
		+	#Determina la posición de los C.I.R. en las cuatro posiciones indicadas en la figura.
		+	#Explica qué tipo de movimiento realiza la barra en cada uno de los instantes correspondientes a dichas posiciones.
	==[[ Base y ruleta de un disco que rueda sin deslizar (G.I.A.) | Base y ruleta de un disco que rueda sin deslizar]]==		==[[ Base y ruleta de un disco que rueda sin deslizar (G.I.A.) | Base y ruleta de un disco que rueda sin deslizar]]==
	[[Imagen:F1_GIA_base_ruleta_disco_enunciado.png|400px|right]]		[[Imagen:F1_GIA_base_ruleta_disco_enunciado.png|400px|right]]
	Determina la base y la ruleta de un disco de radio <math>R</math> que rueda sin deslizar sobre una superficie horizontal. El centro del disco se mueve con velocidad uniforme de módulo <math>v_0</math>.		Determina la base y la ruleta de un disco de radio <math>R</math> que rueda sin deslizar sobre una superficie horizontal. El centro del disco se mueve con velocidad uniforme de módulo <math>v_0</math>.

---

Revisión de 00:00 8 ene 2012

Contenido 1 Biela-manivela 2 Aro con deslizador 3 Disco apoyado en una placa y una pared 4 Barra horizontal sobre un disco 5 Partícula moviéndose radialmente sobre el radio de un disco 6 Disco articulado con una varilla 7 Placa empujando un disco 8 CIR de un velocípedo 9 Barra sobre dos discos que ruedan sin deslizar 10 Disco que arrastra una varilla 11 Disco con varilla articulada 12 Base y ruleta de un disco que rueda sin deslizar

1 Biela-manivela

La figura muestra el mecanismo de biela-manivela. La manivela (sólido "0") gira alrededor del punto O con velocidad angular uniforme ω. La biela (sólido "2") gira alrededor de su punto de unión con la manivela (punto A). El otro extremo de la biela está unido (punto B) al deslizador (sólido "3") que realiza una traslación sobre el eje X₁

Utilizando el triángulo OAB y la descomposición {31}={32}+{20}+{01}, verifica que el movimiento {31} es una traslación.

1. Determina gráficamente la posición de los C.I.R de todos los movimientos del problema.
2. Determina los vectores 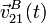y .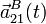

2 Aro con deslizador

Sea un aro de centro C y radio R (sólido "2") que se mueve, en un plano fijo OX₁Y₁ (sólido "1"), de tal modo que está obligado a deslizar en todo instante por un pasador giratorio situado en el punto O, y además se halla articulado en su punto A a un deslizador que se mueve siempre sobre el eje horizontal OX₁ (ver figura). Con carácter auxiliar, se define el sistema de ejes OX₂Y₂ (sólido "2") solidario con el aro en su movimiento. Se pide:

1. Determinar gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
2. Sabiendo que el ángulo θ, que forman los ejes OX₁ y AX₂, verifica la ley horaria θ(t) = ωt (donde ω es una constante conocida), calcular 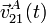y .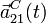

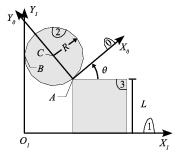
3 Disco apoyado en una placa y una pared

El sistema mecánico de la figura está compuesto por los siguientes sólidos rígidos:

1. Sólido "1": plano fijo O₁X₁Y₁.
2. Sólido "3": placa cuadrada, de lado L, que desliza sobre el eje O₁X₁, manteniendo su lado inferior completo en permanente contacto con él.
3. Sólido "2": disco, de centro en C y radio R que, en todo instante, rueda sin deslizar sobre el eje O₁Y₁ en el punto de contacto B, a la vez que rueda y desliza sobre la placa cuadrada en el punto de contacto A.
4. Sólido "0": sistema de ejes AX₀Y₀, definido de tal modo que el eje AY₀ contiene permanentemente al centro C del disco, mientras que el eje AX₀ es tangente a dicho disco.

En el instante considerado en la figura

1. determina gráficamente la posición de los C.I.R. I₂₁, I₂₀, I₀₃, I₂₃, I₀₁.
2. Utilizando como parámetro el ángulo θ del dibujo (ángulo que forma el eje AX₀ con respecto al lado superior de la placa cuadrada), y teniendo presentes las leyes de composición de velocidades y de velocidades angulares aplicadas a:

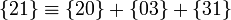
calcula las reducciones cinemáticas en C de los movimientos {20}, {03}, {31} y {21}:

4 Barra horizontal sobre un disco

El sistema de la figura consta de un disco (sólido "0"), de centro O y radio R, que rueda sin deslizar sobre el eje horizontal O₁X₁ del triedro fijo O₁X₁Y₁ (sólido "1"); y de una barra de longitud indefinida (sólido "2"), que se desplaza horizontalmente con velocidad constante v₀, manteniéndose siempre en contacto tangente con el perímetro del disco (punto A) y sin deslizar sobre éste. Halla:

1. Las reducciones cinemáticas de los movimientos {21}, {01} y {20} en el centro del disco (punto O), es decir: 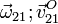, 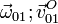y .
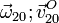2. La aceleración relativa barra-disco del punto de contacto A, es decir, .

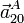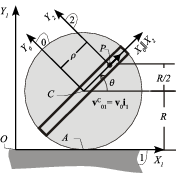
5 Partícula moviéndose radialmente sobre el radio de un disco

Una partícula P recorre con velocidad constante v₀ el diámetro de un disco de radio R (sólido "0"). A su vez, el disco, contenido en todo instante en el plano fijo OX₁Y₁ (sólido "1") rueda sin deslizar sobre el eje OX₁, de tal modo que su centro C avanza con velocidad .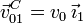

Asociando al disco el triedro solidario CX₀Y₀ (sólido "0"), y definiendo un triedro auxilar PX₂Y₂ (sólido "2") cuyos ejes PX₂ y PY₂ tienen las mismas direcciones que los ejes CX₀ y CY₀, respectivamente; determina, en función de los datos del problema (R y v₀) y de las coordenadas polares que se definen en la figura (ρ y θ):

1. La velocidad absoluta (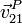) y la aceleración absoluta (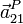) de la partícula P.
2. La posición del C.I.R. del movimiento {21} (analíticamente).

Nota: Se recomienda el uso de la base vectorial asociada al triedro "0" para resolver el ejercicio.

6 Disco articulado con una varilla

El mecanismo de la figura está formado por un disco (sólido "0"), de radio R; y por una varilla OA (sólido "2"), de longitud 2R, articulada en su extremo O al centro del disco. El disco rueda sin deslizar sobre la recta fija (sólido "1") de ecuación y₁ = − R, mientras que el extremo A de la varilla está obligado a deslizar sobre el eje O₁Y₁. Sabiendo que el mecanismo se mueve conforme a la ley horaria θ(t) = ωt (donde ω es una constante conocida), se pide:

1. Los vectores de posición, 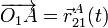; velocidad, 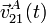; y aceleración 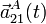, del movimiento absoluto del extremo A de la varilla. ¿Qué tipo de movimiento describe dicho punto?
2. Reducciones cinemáticas (vectores velocidad angular y velocidad de un punto) de los movimientos {21}, {01} y {20}.
3. Determinación gráfica y analítica de la posición del C.I.R. del movimiento {21}.

7 Placa empujando un disco

El cuadrado de la figura (sólido "0") realiza un movimiento plano cuando uno de sus lados desliza sobre un plano horizontal fijo (sólido "1"). El cuadrado empuja a un disco de radio R (sólido "2") que rueda sin deslizar sobre el plano "1".

1. Determine la posición de los C.I.R. de los diferentes movimientos en el instante reflejado en la figura.
2. Determine las reducciones cinemáticas de los movimientos en el instante en que la velocidad absoluta del punto A del sólido "0" es .
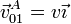3. Si el sistema parte del reposo y el punto A del sólido "0" realiza un movimiento uniformemente acelerado, con aceleración a₀, obtenga la expresión en función del tiempo del vector rotación 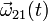y su derivada temporal .
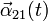4. En las condiciones del apartado anterior, calcule la expresión de la aceleración 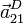, así como la velocidad y aceleración relativa 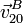y .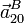

8 CIR de un velocípedo

Los radios de las ruedas delantera (sólido "2") y trasera (sólido "0") de un velocípedo son R y r, respectivamente (R > r); y los puntos de contacto de aquéllas con el suelo (sólido "1") están separados una distancia d. Determinar gráficamente la posición del C.I.R. del movimiento {20}, sabiendo que las dos ruedas del velocípedo ruedan sin deslizar sobre el suelo.

 

9 Barra sobre dos discos que ruedan sin deslizar

Sendos discos de radios radios 2R y R (sólidos “0” y “2”, respectivamente) se encuentran siempre contenidos en el mismo plano y en contacto puntual sobre el sólido fijo “1”. Además, hay una barra rígida (sólido “3”), también contenida en el plano de los discos y en contacto puntual con éstos. El sistema se mueve de manera que los discos “0” y “2” ruedan sin deslizar de manera simultánea sobre los sólidos “1” y “3”.

1. Determine los C.I.R. de los diferentes movimientos relativos en el sistema descrito. ¿Cómo es el movimiento instantáneo de la barra “3” respecto del sólido fijo “1”?
2. Suponiendo que en el movimiento del disco de mayor radio respecto del sólido fijo la velocidad de su centro C es un vector constante de valor conocido 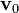, determine las reducciones cinemáticas de los movimientos {01}, {31} y {21}.
3. Determine la ley horaria que sigue la distancia 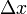entre los puntos de contacto de los discos con el sólido fijo. Supóngase que en el instante inicial esta distancia es 3R.
4. Determine la reducción cinemática del movimiento relativo del disco pequeño respecto del grande, {20}. Calcule la aceleración instantánea del centro D en dicho movimiento.

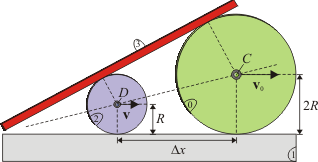
10 Disco que arrastra una varilla

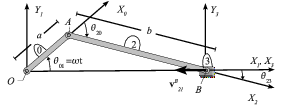
En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio R (sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco, C, se desplaza con una velocidad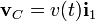 . La barra de longitud 3R (sólido “2”) tiene su extremo C articulado en el centro del disco, mientras que se apoya en el borde O del sólido “1”.

1. Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}.
2. En el instante en que la distancia entre los puntos O y B es igual a R, la velocidad del punto C es 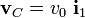. Calcule las reducciones cinemáticas de los tres movimientos en el punto C.
3. Exprese el vector de posición del punto A en el sistema “1”, 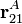, en función de un ángulo β arbitrario.
4. Si 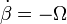, con Ω constante y positiva, calcule 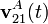y 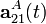para todo instante de tiempo, en función de β, Ω y R.

11 Disco con varilla articulada

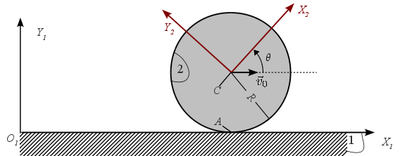
Un disco de radio R (sólido "0"), se mueve contenido siempre en el mismo plano vertical OXY. El centro C del disco realiza un movimiento rectilíneo uniforme con velocidad v₀ respecto del plano horizontal fijo (sólido "1"), sobre el que rueda sin deslizar. Un barra rígida de longitud 4R (sólido "2"), contenida también en OXYZ, tiene su extremo A articulado en un punto del perímetro del disco, mientras que su extremo B se desliza sobre el plano horizontal.

1. Determina la posición de los C.I.R. en las cuatro posiciones indicadas en la figura.
2. Explica qué tipo de movimiento realiza la barra en cada uno de los instantes correspondientes a dichas posiciones.

12 Base y ruleta de un disco que rueda sin deslizar

Determina la base y la ruleta de un disco de radio R que rueda sin deslizar sobre una superficie horizontal. El centro del disco se mueve con velocidad uniforme de módulo v₀.