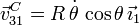Disco apoyado en una placa y una pared (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Determinación gráfica de los CIR
- 2.2 Reducciones cinemáticas

1 Enunciado

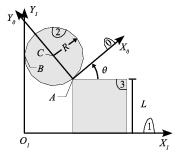
El sistema mecánico de la figura está compuesto por los siguientes sólidos rígidos:

Sólido "1": plano fijo $O 1 X 1 Y 1$ .
Sólido "3": placa cuadrada, de lado $L$ , que desliza sobre el eje $O 1 X 1$ , manteniendo su lado inferior completo en permanente contacto con él.
Sólido "2": disco, de centro en $C$ y radio $R$ que, en todo instante, rueda sin deslizar sobre el eje $O 1 Y 1$ en el punto de contacto $B$ , a la vez que rueda y desliza sobre la placa cuadrada en el punto de contacto $A$ .
Sólido "0": sistema de ejes $A X 0 Y 0$ , definido de tal modo que el eje $A Y 0$ contiene permanentemente al centro $C$ del disco, mientras que el eje $A X 0$ es tangente a dicho disco.

En el instante considerado en la figura

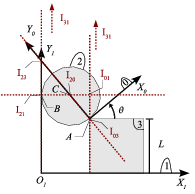
determina gráficamente la posición de los C.I.R. $I 21$ , $I 20$ , $I 03$ , $I 23$ , $I 01$ .
Utilizando como parámetro el ángulo $θ$ del dibujo (ángulo que forma el eje $A X 0$ con respecto al lado superior de la placa cuadrada), y teniendo presentes las leyes de composición de velocidades y de velocidades angulares aplicadas a:

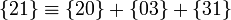
$\{21\} \equiv \{20\}+\{03\}+\{31\}$

calcula las reducciones cinemáticas en $C$ de los movimientos {20}, {03}, {31} y {21}:

2 Solución

2.1 Determinación gráfica de los CIR

Analicemos los datos que tenemos de cada movimiento

2.1.1 Movimiento {21}

El disco rueda sin deslizar en el punto $B$ , entonces este punto es el CIR del movimiento. Por tanto

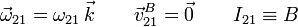
$\vec{\omega}_{21}=\omega_{21}\,\vec{k}\qquad\vec{v}_{21}^B=\vec{0}\qquad I_{21}\equiv B$

2.1.2 Movimiento {31}

La placa se desliza paralelamente al suelo. Por tanto es una traslación pura paralela al eje $O 1 X 1$ :

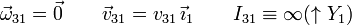
$\vec{\omega}_{31}=\vec{0}\qquad\vec{v}_{31}=v_{31}\,\vec{\imath}_1\qquad I_{31}\equiv \infty (\uparrow Y_1)$

2.1.3 Movimiento {20}

El punto "C" pertenece tanto al sólido "2" como al "0", pues está siempre sobre el eje $A Y 0$ . Por tanto es un punto fijo de este movimiento. Tenemos

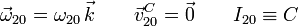
$\vec{\omega}_{20}=\omega_{20}\,\vec{k}\qquad\vec{v}_{20}^C=\vec{0}\qquad I_{20}\equiv C$

2.1.4 Movimiento {03}

El punto "A" pertenece tanto al sólido "3" como al "0", pues está siempre en el punto de contacto entre el disco y la placa. Por tanto es un punto fijo de este movimiento. Tenemos

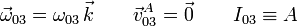
$\vec{\omega}_{03}=\omega_{03}\,\vec{k}\qquad\vec{v}_{03}^A=\vec{0}\qquad I_{03}\equiv A$

2.1.5 Movimiento {23}

El punto $I 23$ está en la intersección de la línea 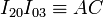$I_{20}I_{03}\equiv AC$ y la línea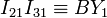 $I_{21}I_{31}\equiv BY_1$

2.1.6 Movimiento {01}

El punto $I 01$ está en la intersección de la línea 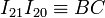$I_{21}I_{20}\equiv BC$ y la línea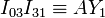 $I_{03}I_{31}\equiv AY_1$

2.2 Reducciones cinemáticas

Debemos determinar las velocidades angulares y velocidades en $C$ en los movimientos de la composición

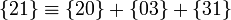
$\{21\} \equiv \{20\} + \{03\} + \{31\}$

En este ejercicio hay que tener cuidado de no dejarse llevar por la intuición y ser sistemáticos. Analicemos con detalle estos movimientos.

2.2.1 Movimiento {03}

Este movimiento es similar al que vimos en el problema 1. El eje $A X 0$ gira con el ángulo $θ$ respecto al sólido "3", así pues

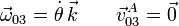
$\vec{\omega}_{03}=\dot{\theta}\,\vec{k}\qquad \vec{v}_{03}^A=\vec{0}$

Como se nos pide la velocidad en $C$ , aplicamos la ecuación del campo de velocidades de {03} para determinarla

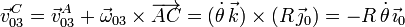
$\vec{v}_{03}^C=\vec{v}_{03}^A+\vec{\omega}_{03}\times\overrightarrow{AC}=(\dot{\theta}\,\vec{k})\times(R\,\vec{\jmath}_0)=-R\,\dot{\theta}\,\vec{\imath}_0$

2.2.2 Movimiento {31}

Esto es una traslación pura, como hemos visto antes. Pero no conocemos la velocidad de la traslación. Por ahora tenemos

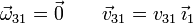
$\vec{\omega}_{31}=\vec{0}\qquad\vec{v}_{31}=v_{31}\,\vec{\imath}_1$

No particularizamos la velocidad en un punto, pues en todos ellos la velocidad es la misma.

2.2.3 Movimiento {20}

Este movimiento es una rotación con centro en $C$ , pero no conocemos su velocidad angular. Tenemos

$\vec{\omega}_{20}=\omega_{20}\,\vec{k}\qquad\vec{v}_{20}^C=\vec{0}$

2.2.4 Movimiento {21}

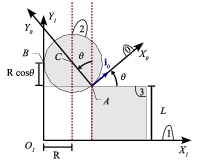
En este caso el CIR es el punto de contacto $B$ entre el disco y la pared. Podemos determinar la posición de $C$ respecto al triedro en reposo "1", y a partir de ahí calcular la velocidad absoluta. De la figura adjunta vemos que

$\begin{array}{l} \overrightarrow{O_1C} = R\,\vec{\imath}_1 + (L+R\,\cos\theta)\,\vec{\jmath}_1\\ \\ \vec{v}_{21}^C=\left.\dfrac{\mathrm{d}\overrightarrow{O_1C}}{\mathrm{d}t}\right|_1=-R\,\dot{\theta}\,\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 \end{array}$

Por otro lado la velocidad en $B$ es cero pues es un punto fijo del movimiento. Entonces

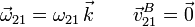
$\vec{\omega}_{21}=\omega_{21}\,\vec{k}\qquad\vec{v}_{21}^B=\vec{0}$

Con la ecuación del campo de velocidades relacionamos 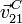$\vec{v}_{21}^C$ y $\vec{v}_{21}^B$ y calculamos $ω 21$

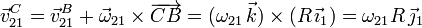
$\vec{v}_{21}^C=\vec{v}_{21}^B+\vec{\omega}_{21}\times\overrightarrow{CB}=(\omega_{21}\,\vec{k})\times(R\,\vec{\imath}_1)=\omega_{21}R\,\vec{\jmath}_1$

Comparando las dos velocidades obtenemos la reducción

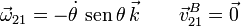
$\vec{\omega}_{21}=-\dot{\theta}\,\,\mathrm{sen}\,\theta\,\vec{k}\qquad\vec{v}_{21}^B=\vec{0}$

2.2.5 Aplicación de la composición {21}={20} + {03} + {31}

Podemos ahora aplicar esta composición para encontrar las magnitudes que nos faltan. Para las velocidades angulares tenemos

$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{03}+\vec{\omega}_{31}$

Aquí no conocemos $\vec{\omega}_{20}$ . Despejando

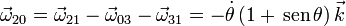
$\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{03}-\vec{\omega}_{31} = -\dot{\theta}\,(1+\,\mathrm{sen}\,\theta)\,\vec{k}$

Para las velocidades

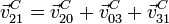
$\vec{v}_{21}^C=\vec{v}_{20}^C+\vec{v}_{03}^C+\vec{v}_{31}^C$

En este caso la incógnita es 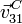$\vec{v}_{31}^C$ . Despejando

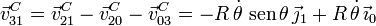
$\vec{v}_{31}^C=\vec{v}_{21}^C-\vec{v}_{20}^C-\vec{v}_{03}^C=-R\,\dot{\theta}\,\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 + R\,\dot{\theta}\,\vec{\imath}_0$

Tenemos que expresar 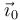$\vec{\imath}_0$ en la base del triedro "1". Observando la última figura vemos que

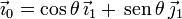
$\vec{\imath}_0 = \cos\theta\,\vec{\imath}_1+\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Por tanto

$\vec{v}_{31}^C=R\,\dot{\theta}\,\cos\theta\,\vec{\imath}_1$

Disco apoyado en una placa y una pared (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Determinación gráfica de los CIR

2.1.1 Movimiento {21}

2.1.2 Movimiento {31}

2.1.3 Movimiento {20}

2.1.4 Movimiento {03}

2.1.5 Movimiento {23}

2.1.6 Movimiento {01}

2.2 Reducciones cinemáticas

2.2.1 Movimiento {03}

2.2.2 Movimiento {31}

2.2.3 Movimiento {20}

2.2.4 Movimiento {21}

2.2.5 Aplicación de la composición {21}={20} + {03} + {31}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES